单层VAE原理与置信下界

VAE的原理大概为，给定一个 $x$，我们认为其是由一个隐变量 $z$ 生成的，这个隐变量 $z$ 则是通过一个后验网络 $q_{\phi}(z|x)$ 预测出来的，而在推理的时候，则是通过 $z$ 去预测 $x$.

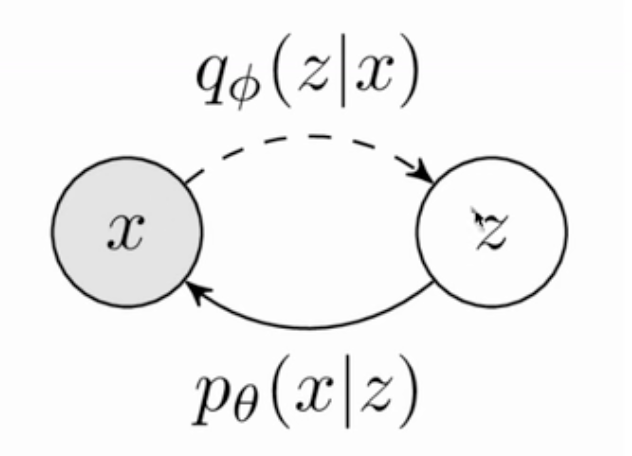
如果用公式描述$p(x)$的生成过程，则大概可以分为以下几步

$p(x) = \int_z p_{\theta}(x|z)p(z) \tag{1}$

可以理解为在所有 $z$ 上进行积分得到每一个 $p(z)$ 发生的概率乘以每一个 $p(z)$ 发生的时候 $p(x)$ 也发生的概率 $p_\theta(x|z)$，此时我们同时乘以和除以一个 $q_\phi(z|x)$，则可以得到：

$p(x) = \int_z q_\phi(z|x) \frac{p_{\theta}(x|z)p(z)}{q_\phi(z|x)} \tag{2}$

我们可以把这个边缘计算进行期望表示

$logp(x)=logE_{z \sim q_\phi(z∣x)} [\frac{p_\theta(x∣z)p(z)}{q_\phi(z∣x)}] \tag{3}$

对于这个 将边缘计算进行期望表示 即公式(3) 的理解为：

对于一个连续随机变量 $Z$ 和一个函数 $f(Z)$，其期望（均值）定义为：

$\mathbb{E} = \int_{-\infty}^{\infty} f(z)p(z) dz \tag{4}$

其中：

• $f(Z)$ 是随机变量 $Z$ 的某个函数
• $p(z)$ $Z$ 的概率密度函数

这个公式表明，期望是通过将函数 $f(Z)$ 在整个样本空间上加权平均得到的，权重上随机变量的概率密度 $p(z)$。

假如有一个积分表达式：

$I=\int f(z)g(z)dz \tag{5}$

如果我们将 $g(z)$ 视为某个随机变量 $Z$ 的概率密度函数 $p(z)$，那么这个积分可以写成

$I=\int f(z)p(z) dz \tag{6}$

根据期望的定义，这正是随机变量 $f{Z}$的期望：

$I=\mathbb{E}[f(Z)] \tag{7}$

则对于我们的边缘计算进行期望表示则可以理解为：

$\int f(z)q_\phi(z|x)dz = \mathbb{E}_{z \sim q_\phi(z|x)}[f(z)] \tag{8}$

即在给定条件 $x$ 下，随机变量 $f(Z)$ 的期望可以通过积分计算，$z \sim q_\phi(z∣x)$ 是概率论和机器学习中常见的表示方法。它表示随机变量 $z$ 从条件概率分布 $q_\phi(z∣x)$ 中采样。

根据公式(8)，我们可以将 $\frac{p_{\theta}(x|z)p(z)}{q_\phi(z|x)}$ 看作是 $f(z)$，则$f(z)$可以被写为

$f(z)=\frac{p_{\theta}(x|z)p(z)}{q_\phi(z|x)} \tag{9}$

则公式(2)可以被写为：

$p(x) = \int_z q_\phi(z|x) f(z) \tag{10}$

那么则有：

$logp(x)=logE_{z \sim q_\phi(z∣x)} f(z) \tag{11}$

根据詹森不等式（Jensen’s Inequality），将对数期望转换为一个下界。这个下界被称为证据下界（Evidence Lower Bound, ELBO），它是变分推断中优化的目标。
詹森不等式的定义：对于一个凸函数$f$和一个随机变量$X$，詹森不等式表述为，如果$f$是一个凸函数，那么对于任何随机变量$X$，我们有：

$f(\mathbb{E}[X]) \leq \mathbb{E(f(X))} \tag{12}$

当 $f()==log()$时候，通过最大化 ELBO，我们可以找到最佳的近似分布 $q_\phi(z∣x)$，从而使其尽可能接近真实的后验分布 $p(z∣x)$。

$logp(x) = logE_{z \sim q_\phi(z∣x)} f(z) \\ \geq \mathbb{E}_{z \sim q_\phi(z∣x)} [\log f(z)] \tag{13}$

其中：

$f(z) = \frac{p_{\theta}(x|z)p(z)}{q_\phi(z|x)} \tag{14}$

综上，则有：

$log p(x) \geq \mathbb{E}_{z \sim q_\phi(z∣x)} [\frac{p_{\theta}(x|z)p(z)}{q_\phi(z|x)}] \tag{15}$