机器学习-梯度下降的优化
在回归中,我们需要解决下面的优化问题,即使得Loss函数尽可能的小
\[ \theta^*=arg\min L(\theta),L:loss function,\theta:parameters \]
假设一共有两个参数\(\theta_1,\theta_2\),使得\(\theta^0= \begin{bmatrix}\theta^0\\\theta^1\end{bmatrix}\),便有梯度如下
\[\nabla L(\theta)=\begin{bmatrix} \partial L(\theta_1)/ \partial \theta_1\\\ \partial L(\theta_2)/ \partial \theta_2\end{bmatrix}\]
那么参数的更新便可通过向量的形式进行
\[ \begin{bmatrix}\theta^1_1\\\theta^1_2\end{bmatrix}=\begin{bmatrix}\theta^0_1\\\theta^0_2\end{bmatrix}-\eta\begin{bmatrix} \partial L(\theta^0_1)/ \partial \theta_1\\\ \partial L(\theta^0_2)/ \partial \theta_2\end{bmatrix} \]
但是其中,\(\eta\)是一直不变的,但是我们知道,经过迭代之后,在越来约接近目标的时候,我们需要将学习率降低,使其能够愈发趋近目的地。故,我们对\(eta\)进行改进,使其经过一定的迭代后越来越小。
\[ \eta^t=\eta/\sqrt{t+1} \]
但是学习率不能一刀切,对于参数,我们也需要给予其一定的改变。一般我们的参数的改变为
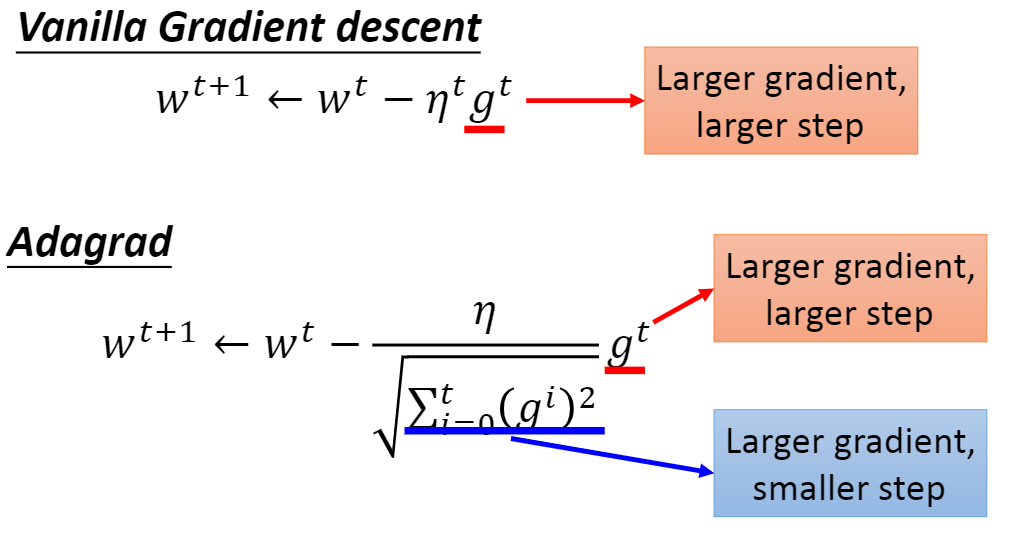
\[ w^{t+1}=w^t-\eta^tg^t \]
w是一个参数,我们设置\(\eta^t\) 为参数w之前导数的均方根,使其成为一个参数依赖型的学习率。也就是说
\[ w^1=w^0-\frac{\eta^0}{\sigma^0}g^0,\sigma^0=\sqrt{(g^0)^2}\\ w^2=w^1-\frac{\eta^1}{\sigma^1}g^1,\sigma^1=\sqrt{\frac{1}{2}[(g^0)^2+(g^1)^2]}\\ \]
如此迭代,直到
\[ w^{t+1}=w^t-\frac{\eta^t}{\sigma^t}g^t,\sigma^t=\sqrt{\frac{1}{t+1}\sum^t_{i=0}(g^i)^2} \]
从上面的式子中,我们可以看到\(\eta^t\)是一个时间相关的学习率,\(\sigma^t\)是一个参数相关的学习率,且
\[ \eta^t=\frac{\eta}{\sqrt{t+1}},\sigma^t=\sqrt{\frac{1}{t+1}\sum^t_{i=0}(g^i)^2} \]
故相除之后得到下列的公式
\[ w^{t+1}=w^t-\frac{\eta}{\sqrt{\sum^t_{i=0}(g^i)^2}}g^t \]
梯度改进之后的对比如下: