概览

成排的GPU集群发出整齐划一的轰鸣，这正是训练当代顶尖AI模型所需的场景——一场算力交响曲的演绎，而这般景象在不久前还只是顶尖实验室的专利。开源运动虽然打破了技术垄断，却未能完全消弭核心壁垒。如今，任何人都能自由下载最新的Llama或DeepSeek模型，研读其技术文档和实验报告。但真正的精要所在——那套驾驭GPU集群训练庞然智能体的工程体系，那些在分布式系统中精妙调谐万千计算单元的核心技艺——仍如深藏云端的圣殿，其奥义散落在晦涩难懂的学术论文与彼此割裂的私有代码库之间，构筑着难以逾越的技术鸿沟。

这本开源书籍旨在引领变革。从基础出发，我们将引导你掌握将大型语言模型训练从单 GPU 扩展到数十、数百甚至数千 GPU 所需的知识，并通过实际代码示例和可复现的基准测试来阐述理论，使内容更加自然易懂。

随着训练模型所用的集群规模不断扩大，人们发明了多种技术，包括数据并行(Data Parallel, DP)、张量并行(Tensor Parallel, TP)、流水线并行(Pipeline Parallel, PP)和上下文并行(Context Parallel，以及 ZeRO 或内核融合(Kernel Fusion)，以确保 GPU 始终高效运行。这大大缩短了训练周期，并充分利用了昂贵的硬件资源。

更有甚者，随着 AI 训练扩展的挑战超越了仅仅构建初始模型，团队发现，在特定数据上对大型模型进行微调往往能取得最佳效果，通常采用相同的分布式训练技术。

在本书中，我们将逐步介绍所有这些技巧——从最简单的到最精致的——同时保持一个主线故事，以便理解每种技巧的来源。

我们假设你对当前LLM架构有一些基本的了解，并对深度学习模型的训练方法有所熟悉，但分布式训练可能对你来说还是陌生的。如有需要，你可以在 DeepLearning.ai 或 PyTorch 教程部分找到有关模型训练基础知识的优质课程。

本书可以看作是我们关于数据预处理预训练的第一篇博客（即所谓的“FineWeb blog post”[1]）的续篇。阅读完这两篇博客后，你应该已经掌握了理解当今如何构建LLMs所需的大部分核心知识，只是缺少一些关于数据融合和架构选择的细节来完善整个方案（敬请期待第三部分……）。

这本书立足于以下三个基本原则：

一、 快速了解理论和概念：在深入代码和实验之前，我们希望先了解每种方法在宏观层面上的运作原理及其优缺点。你将学习到哪些部分的语言模型会消耗内存资源，以及这种消耗通常发生在训练的哪个阶段。你还将了解到，我们可以通过并行化模型来克服内存限制，并通过增加 GPU 的规模来提升处理能力。因此，你将明白如何使用以下组件来计算 Transformer 模型的内存分解情况：（编者注：访问https://huggingface.co/spaces/nanotron/ultrascale-playbook 进行体验）

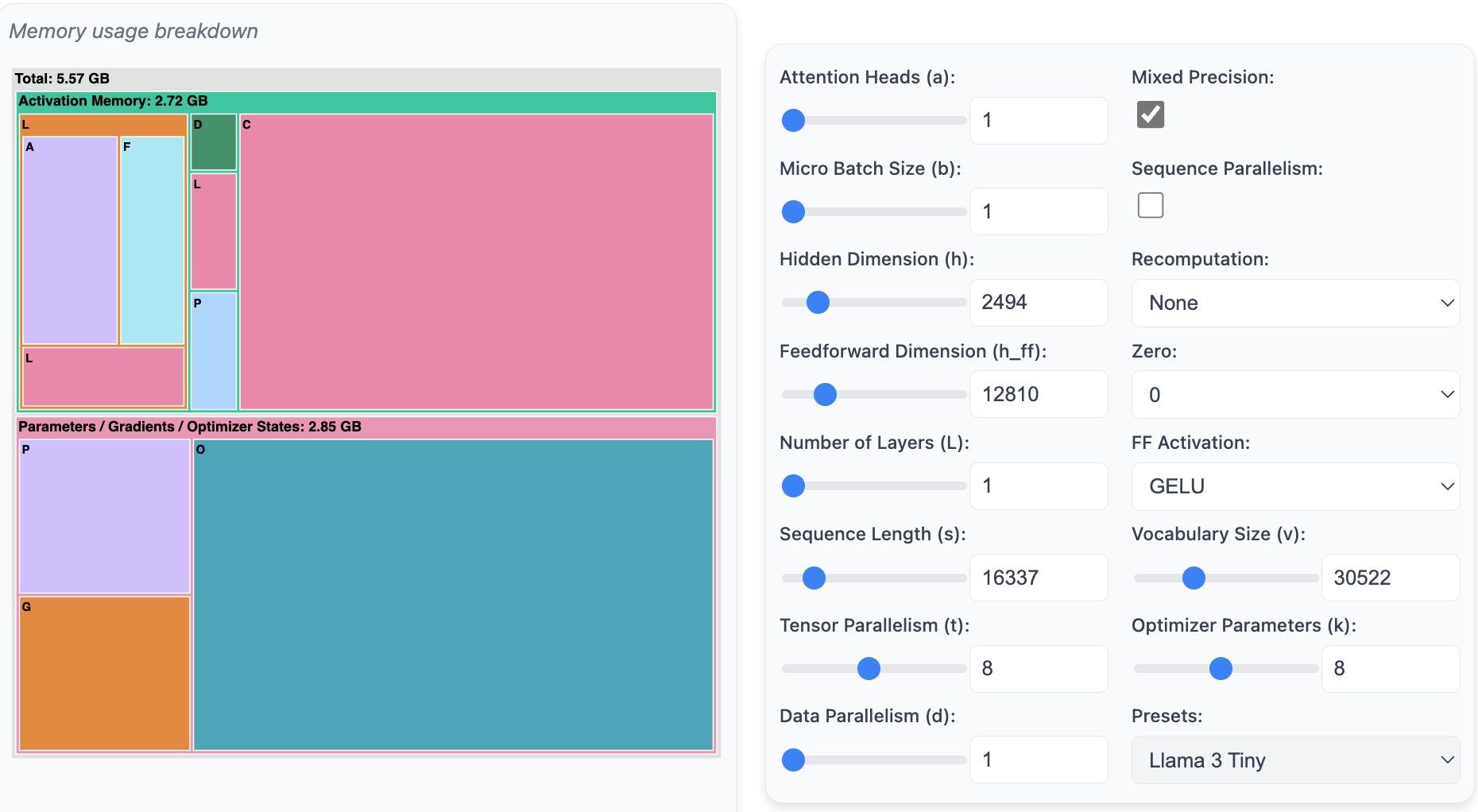
我们还开发了一个工具，可以用来预测训练过程中的内存消耗情况：

**二、 清晰的代码实现：**理论固然重要，但在实际编码过程中，我们会遇到各种边缘情况和关键细节。因此，我们会在可能的情况下提供实现参考链接。根据具体情况，我们可能会引用两种代码示例：

  • Picotron [2] 代码库是为教育而构建的，因此它通常在单个, self-contained 的短文件中实现概念。
  • 另一方面，为了查看可用于生产的代码，我们将参考 nanotron [3] 的实现，这是 Hugging Face 在生产训练中使用的代码库。

三、 真实训练效率基准：最后，如何根据你的硬件设施（例如芯片类型、互连等）实际扩展你的LLM训练规模，我们无法给出一个统一的解决方案。不过，我们将提供一种评估多种配置的方法，这正是我们在我们的集群上所进行的实践！我们进行了超过 4100 次分布式实验（包括测试运行超过 16k 次），并使用了最多 512 个 GPU 来扫描多种可能的分布式训练架构和模型规模。

如你所见，有很多内容需要探讨。在深入分布式训练的细节之前，我们先简要了解一下本书将要讨论的挑战。

High level overview  高级概览

本书将探讨的所有技术都旨在解决以下三个主要挑战之一或多个，这些挑战将在全书的学习过程中不断遇到：

  • 内存使用：这是一个严格的限制——如果训练步骤无法装入内存，则训练无法继续进行
  • 计算效率：我们希望硬件大部分时间用于计算，因此需要降低数据传输时间或等待其他 GPU 执行任务的时间，以提升效率。
  • 通信开销：我们希望尽量减少通信开销，因为它会导致 GPU 闲置。为此，我们将努力最大化利用节点内（快速）和节点间（较慢）的带宽，并尽可能地将通信与计算过程重叠。

在许多地方，我们会发现可以用其中之一（计算、通信、内存）来交换另一个（例如，重新计算或张量并行）。找到合适的平衡是扩展训练的关键。这样的表述更加自然，易于理解。

由于这本书内容非常丰富，我们特别制作了一张速查表，方便你浏览书籍并掌握核心要点。在你面对挑战时，请将它牢记于心！

速查表：

并行策略速查表：

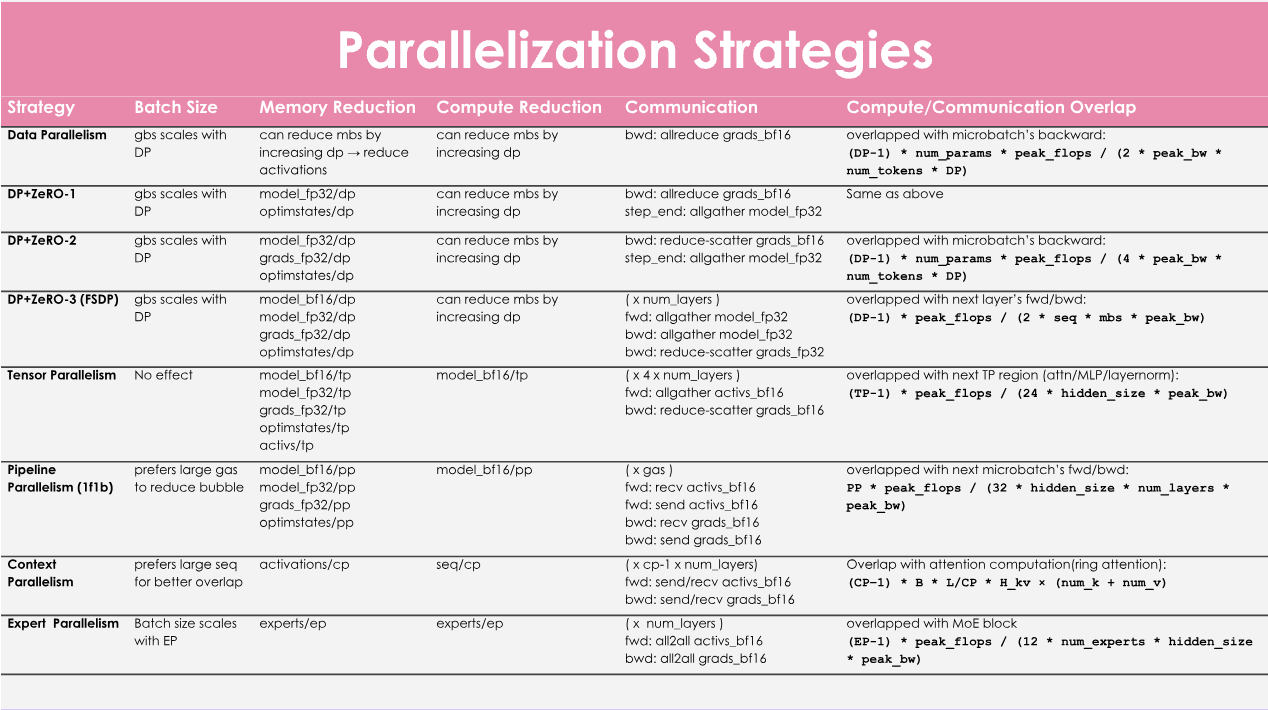
术语表：

并行化术语

  • tp：张量并行度
  • pp：流水线并行度
  • dp：数据并行度
  • cp：上下文并行度
  • ep：专家并行度
  • dp_if_zero1/2/3：使用ZeRO阶段时的有效数据并行度
    （如果使用ZeRO2，则表示dp_if_zero1和dp_if_zero2都使用）

Batch Size术语

  • mbs：每个GPU的微批量大小
  • gas：梯度累积步数
  • mseqlen：每个GPU的序列长度（在CP之后）
  • gbs：全局批量大小 = mbs dp gas * mseqlen

内存术语

  • model_bf16：bfloat16格式的模型参数 = model_bf16(model_config.tp.pp.dp_if_zero3)
  • model_fp32：float32格式的模型参数（用于优化器） = 2 * model_bf16 / dp_if_zero1
  • grads_fp32：float32格式的梯度 = 2 * model_bf16 / dp_if_zero2
  • optimstates：优化器状态（例如，Adam动量/方差）在float32中 = 4 * model_bf16 / dp_if_zero1
  • activs：前向传递中的激活张量 = activs(model_config.mseqlen, mbs, tp, cp, pp, dp_if_zero3)

实用公式

每个GPU在训练步骤中的峰值内存使用量可以近似为：

$$
\text{peak_memory} = \text{model_bf16} + \text{model_fp32} + \text{grads_fp32} + \text{optimstates} + \text{activs}
$$

其中

$$
\text{model_bf16} = \text{bf16_bytes} \times \text{num_params} = 2 \times \text{num_layers} \times 16 \times \text{hidden_size}^2
$$

每个GPU在训练步骤中的计算量可以近似为：

$$
\text{compute} = 6 \times \text{model_bf16} \times \text{mbs} \times \text{seq} \times \text{gas}
$$

第一步：在单个GPU上训练

让我们从快速回顾模型训练的基础知识开始，然后再扩展到多个 GPU。当模型在单个 GPU 上训练时，通常包括以下三个步骤：

  1. 通过模型传递输入以产生输出的前向传播
  2. 反向传播计算梯度
  3. 利用梯度更新参数

它看起来大致如此：

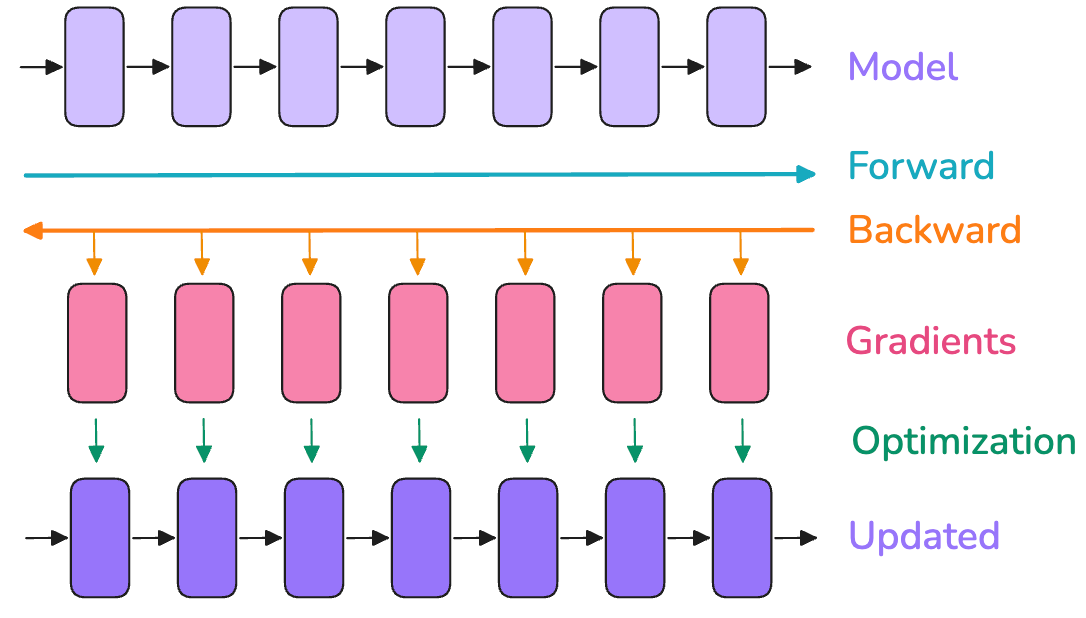
在这个图中，

  • 顶部行的方框可以看作是模型内部连续的层（最后一行也是如此）。
  • 红色方框代表这些层在反向传播过程中计算得到的关联梯度。

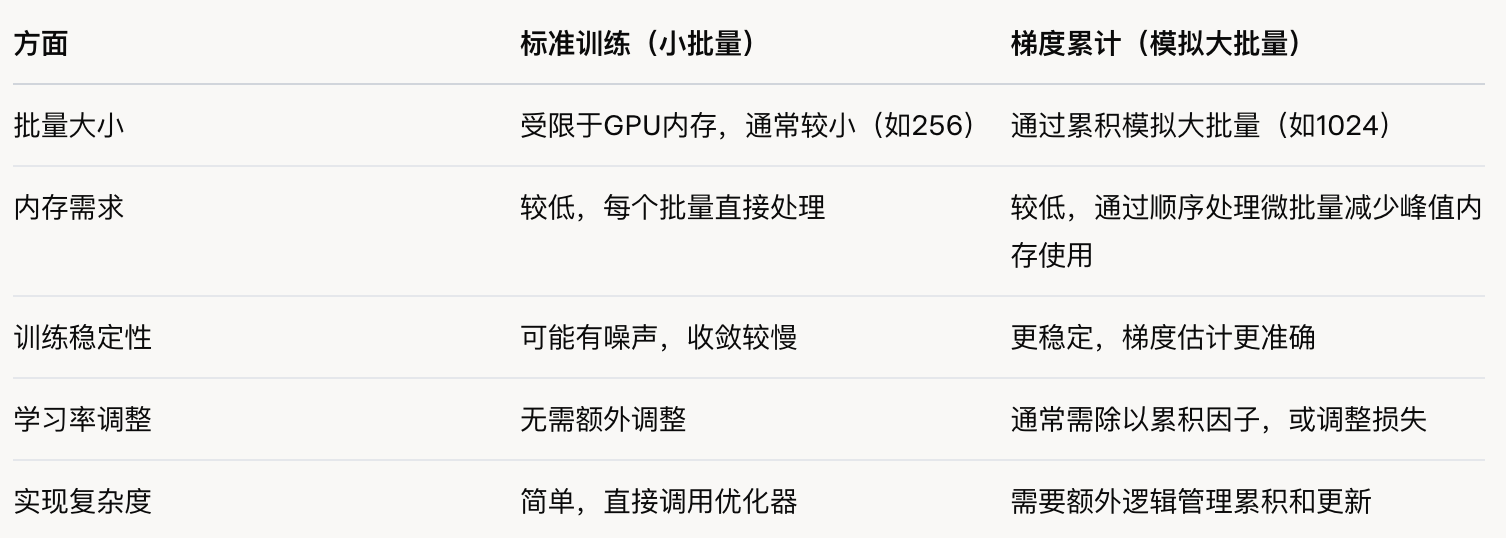
批处理大小（bs）是模型训练中的一个关键超参数，它不仅影响模型的收敛速度，还会对模型的处理能力产生影响。

在训练初期，小批量（batch size）可以快速地在training landscape中移动，从而快速达到一个较优的学习点。然而，在训练的后期，小批量会导致梯度保持较高的噪声，模型可能无法收敛到最优的最终性能。

在另一个极端，大批量虽然能够提供非常准确的梯度估计，但会降低每个训练样本的利用率，导致收敛速度变慢，并且可能会浪费计算资源。关于这个话题的早期讨论，你可以参考OpenAI关于大批量训练的论文或者MiniMax技术报告[4]

Batch size会影响在特定文本数据集上训练所需的时间：batch越小，训练相同样本所需的优化器步数就越多。优化器步数（在计算时间上）成本较高，因此与使用较大的batch size相比，总的训练时间会增加。但要注意，batch size通常可以在最佳batch size附近进行较大调整，而对模型性能的影响不大，也就是说，模型性能对确切batch size值的敏感性通常在最佳batch size附近较低。

编者注：在训练机器学习模型时，选择一个合适的batch size是很重要的。尽管如此，当batch size接近于某个最佳值时，模型的最终性能通常不会对batch size的精确值特别敏感。这意味着，即使batch size稍微有所调整，只要在最佳值附近，模型的性能也不会有显著变化。这种情况使得在实际应用中，我们可以在一定范围内灵活地选择batch size，而不必过于担心对模型性能的影响。

在LLM预训练社区中，batch size通常以 token 数量来报告，而不是样本数量（bst=batch size tokens），这使得训练数量通常与训练时使用的具体输入序列长度无关。

在最简单的情况下，如果是在单机上进行训练，可以通过以下方式从模型输入序列长度（seq）计算出 bs（样本数量）和 bst(batch size tokens)：

$$
bst=bs\times seq
$$

从这里开始，我们将以样本为单位展示batch size的公式，但你始终可以通过将其乘以序列长度来获得其以token为单位的对应值。

最近的大型语言模型训练的理想点通常是每batch大约 4-60 million token per batch。batch size和训练语料库多年来一直在稳步增加：Llama 1 使用约 4M token的batch size训练了 1.4T tokens，而 DeepSeek 使用约 60M token的batch size训练了 14 T tokens。

在将模型训练扩展到大规模batch时，我们面临的首要挑战是内存不足问题。当我们的 GPU 内存不足以容纳目标batch大小时，我们该如何应对？

让我们先快速了解导致我们最初出现内存不足问题的原因。这将帮助我们获得一些关于训练模型内存需求的宝贵直觉。

Transformer的内存使用情况

在训练神经网络模型时，人们会在内存中存储多个项目：

  • Model weights 模型权重
  • Model gradients 模型梯度
  • Optimizer states 优化器状态
  • Activations needed to compute the gradients 计算梯度所需的激活数量

你可能会觉得对于一个模型，理论上应该可以精确计算出内存需求，但实际中存在一些额外的内存占用因素，这使得精确计算变得困难：

  • CUDA 内核通常需要 1-2GB 的 GPU 内存，你可以通过运行 import torch; torch.ones((1, 1)).to("cuda") 并检查 nvidia-smi 中的 GPU 内存来快速确认。
  • 来自缓冲区、中间结果以及因碎片化而无法使用的部分内存的休息内存使用情况

我们将忽略以上两者，因为它们通常很小且为常数项。

这些项目以张量（Tensor)形式存储，具有不同的形状和精度。

  • 形状由超参数确定，如batch size bs、序列长度 seq、模型隐藏维度hid、注意力头head、词汇量大小以及我们稍后将要看到的潜在模型分片(model sharding)。
  • 精度指的是 FP32、BF16 或 FP8 等格式，分别需要 4、2 或 1 个字节来存储张量中的每个单独值。

我们将在混合精度训练部分全面讨论不同的精度及其权衡，现在只需记住，这些不同格式的内存需求将不同，这将影响我们需要存储的项目内存使用。

所以，我如何快速确定这些变量的内存使用情况？一种简单的方法是进行经验测量。

分析内存使用 Profiling

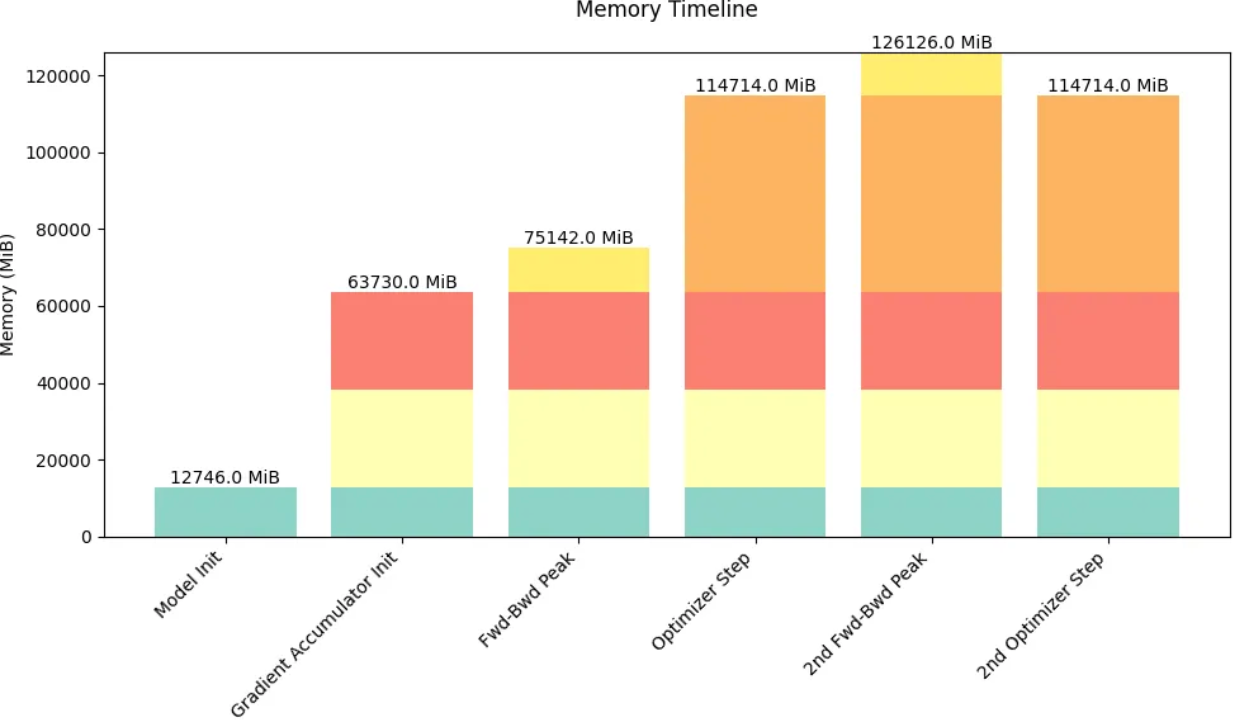
使用 PyTorch Profiler，我们可以了解在整个训练过程中内存是如何分配的。我们可以看到，内存利用率不是一个静态的东西，而是在训练过程中以及训练步骤中变化很大。

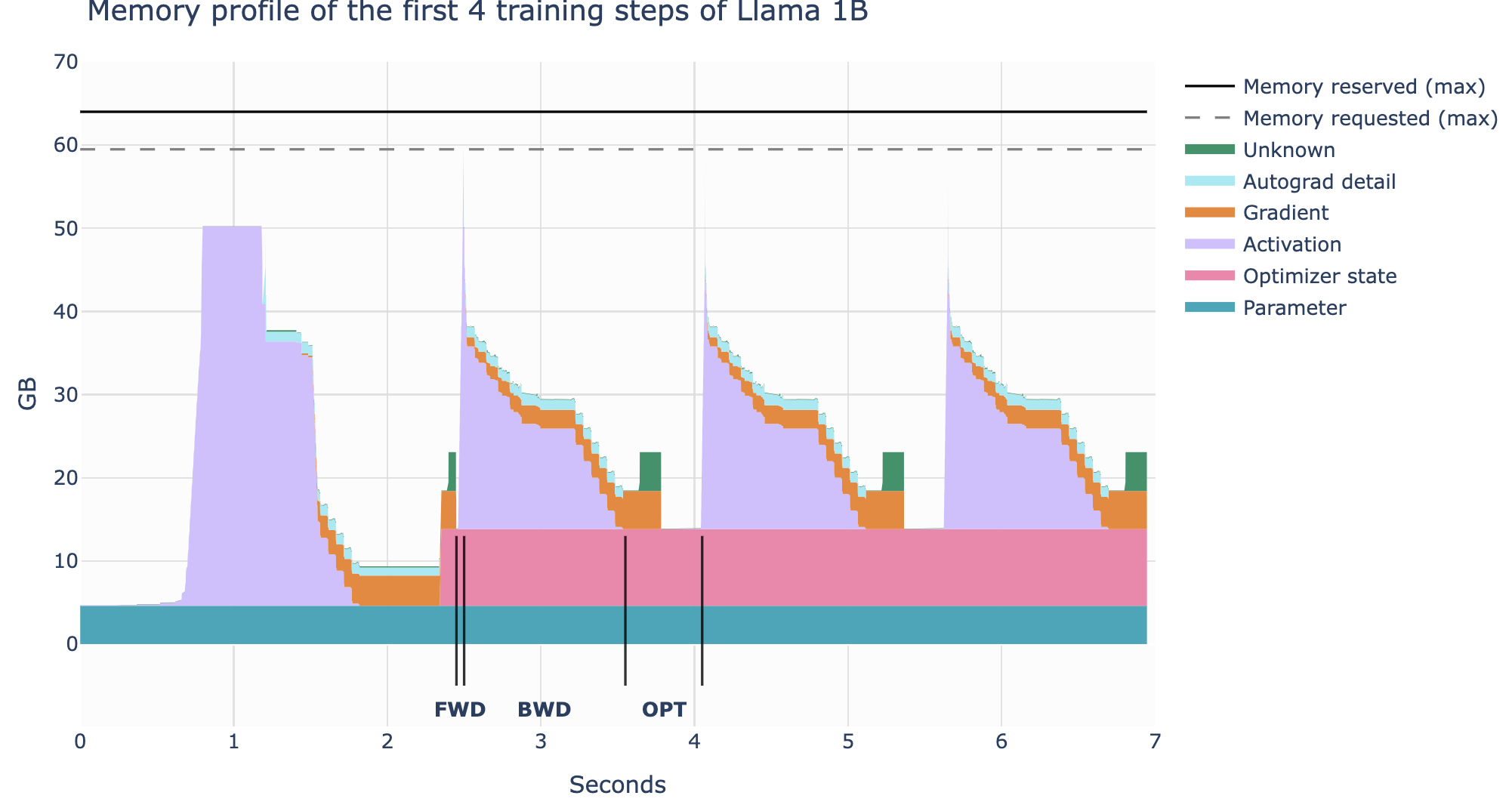
显然，第一步看起来与后续步骤非常不同，但让我们首先看看一个步骤的一般结构：

  • 在前向传播时激活值迅速增加，
  • 在反向传播时梯度累积，
  • 随着反向传播的进行，用于计算梯度的存储激活值逐渐被清除。
  • 执行优化步骤，在此期间我们需要所有的梯度，
  • 更新优化器状态，
  • 开始下一次前向传播。

为什么第一步看起来不同：激活值迅速增加然后保持一段时间。在这个第一步中，torch 缓存分配器做了很多准备工作，准备内存分配以加快后续步骤，这样就不需要在之后搜索空闲内存块（参见 Zach 的博客[5]）。在第一步之后，我们还看到优化器状态的出现，这通常会抵消进一步训练步骤的内存使用。

现在我们已经对内存有了初步的了解，让我们看看如何扩大训练规模通常是一个在保持这些各种项目（激活、参数、梯度、优化器状态）内存需求在 GPU 内存限制内的问题，即最大化计算效率。

权重/梯度/优化器状态内存

让我们从我们列表中的前 3 个项目开始：模型的权重Weight、梯度Gradient和优化器Optimizer状态。实际上，我们可以相当容易地估算出它们所需的内存。

对于简单的 Transformer LLM，参数数量由以下公式[6]给出：

$$
N=h\times v+L\times(12\times h^2+13\times h)+2 \times h
$$

在该方程中， h 是隐藏维度， v 是词汇量大小， L 是模型中的层数。

注意，观察方程我们可以看到，在大的隐藏维度下将占主导地位的项是 $h^2$ 项，因为它是我们调整参数时唯一一个呈二次增长的项。

内存需求仅是参数数量乘以每个参数的字节数。在传统的全精度（FP32）训练中，参数和梯度都需要 4 个字节，而如果使用 Adam 优化器，则需要存储动量和方差，这为每个参数额外增加了两个 4 个字节的存储。总之：

$$
m_{params} = 4 \times N \
m_{grad} = 4 \times N \
m_{opt} = (4 + 4) \times N
$$

现在让我们看看如果我们使用更低的精度会发生什么变化。出于稳定性的原因，我们通常不使用完全的低精度训练，而是使用称为“混合精度”, 即同时采用更高和更低精度的组合。

现在混合精度训练的默认做法是，对于大多数计算通常使用 BF16，每个参数和梯度需要 2 个字节，以及额外的 FP32 模型权重和梯度的副本，因此每个参数总共需要 12 个字节。除了参数和梯度，我们还需要存储优化器的状态：对于 Adam 优化器，这需要动量和方差，通常以 FP32 存储以提高数值稳定性，每个使用 4 个字节。如下图：

组件类型 数据类型 每个参数/分量的字节大小 说明
参数（主副本） BF16 2 字节 BF16用于大多数计算
参数（FP32副本） FP32 4 字节 用于存储FP32精度的模型权重副本
梯度（主副本） BF16 2 字节 BF16用于梯度计算
梯度（FP32副本） FP32 4 字节 用于存储FP32精度的梯度副本
Adam优化器状态（动量） FP32 4 字节 动量值，以FP32存储以提高数值稳定性
Adam优化器状态（方差） FP32 4 字节 方差值，以FP32存储以提高数值稳定性

总结如下：

$$
m_{\text{params}} = 2 \times N \
m_{\text{grad}} = 2 \times N \
m_{\text{params_fp32}} = 4 \times N \
m_{\text{opt}} = (4 + 4) \times N
$$

注意：

一些库将梯度存储在 fp32 中，这将需要额外的

mparams_fp32=4xN内存。例如在 nanotron 中这样做，因为bf16对于较小的值是损失性的，我们始终优先考虑稳定性。有关更多信息，请参阅此 DeepSpeed 问题[7]。FP32 参数副本也被称为 “主权重 Master Weights”

有趣的是，混合精度本身并不节省整体内存，因为它只是将内存以不同的方式分配到三个组件中，而且如果我们以 FP32 累积梯度，实际上还会比全精度训练多出 4 个字节。

尽管如此，它仍然具有优势，因为以半精度计算正向/反向传递使我们能够

（1）在 GPU 上使用优化的低精度操作，这些操作更快

（2）减少正向传递期间的激活内存需求.

让我们了解一个模型（全精度和混合精度给出相同总体值）需要多少通用内存：

随着我们可以看到，一旦我们达到 7B，权重和优化器需求已经开始显著增加，并超过典型 GPU 内存的大小，例如 H100 GPU 的 80GB。

但现在，让我们从仍然可以适应单个 GPU 的模型开始，看看对我们内存预算贡献最大的因素：激活内存 Activation Memory。

Activation Memory 激活内存

激活内存的计算比权重、梯度和优化器状态要复杂一些，部分原因在于它依赖于模型的输入。如果你不确定为什么我们需要存储反向传播中的激活，这篇参考资料[8]是一个很好的快速回顾。在仔细检查了反向传播的计算方式之后，我们可以估算出在混合精度下激活所需的总内存，并得出以下方程：

$$
m_{\text{act}} = L \cdot \text{seq} \cdot \text{bs} \cdot h \cdot \left(34 + \frac{5 \cdot n_{\text{heads}} \cdot \text{seq}}{h}\right)
$$

这里 L 是层数， $\text{seq}$ 是序列长度， bs 是样本batch size， h 是模型的隐藏维度， $n_{\text{heads}}$ 是注意力头数。详细推到请参考[9]

这里一个有趣的观察是，对于给定的模型，其内存不是静态的，而是与序列长度和batch size成线性关系。这意味着激活内存是当我们增加batch size或使用更长的序列进行训练时将会膨胀的部分。我们可以使用这个方程来查看不同序列长度（例如 Llama 模型）的内存使用情况（ bs=1 ）。

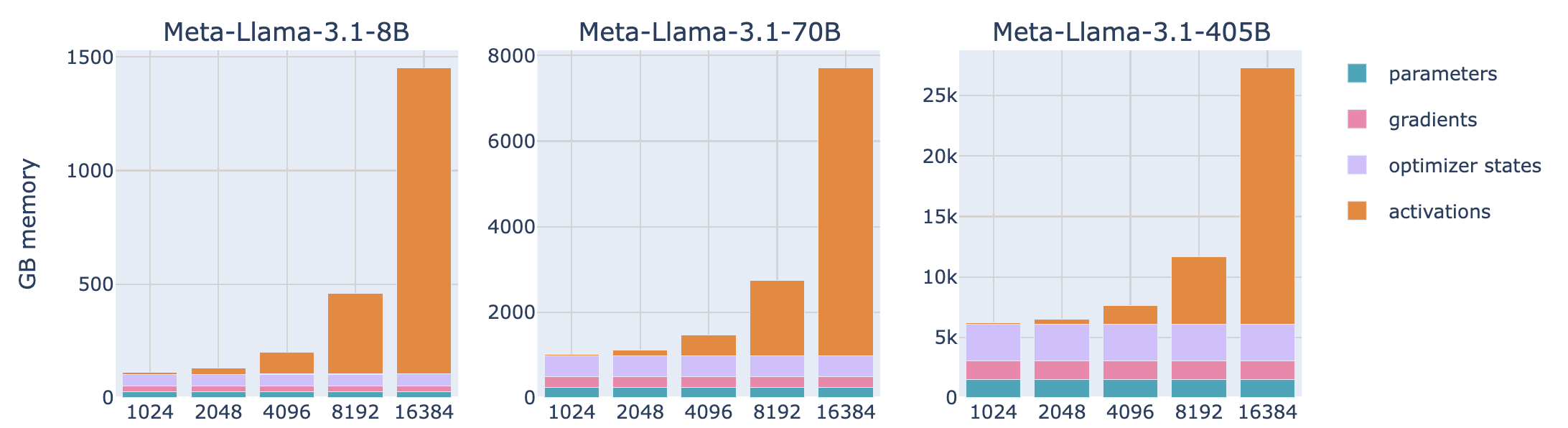
这张图讲述了一个引人注目的故事：对于短序列（或类似的小batch size），激活几乎可以忽略不计，但大约在 2-4k 个token处，它们开始占用相当大的内存，而参数、梯度和优化器状态的使用与序列长度和batch size基本独立。

对于大型输入标记（即大型batch size/序列），激活函数成为最大的内存负担。

有没有办法驯服这种“激活爆炸”？是时候来解释我们的第一种技术——称为激活重计算（Activation Recomputation）——它将帮助我们限制激活内存占用。今天大型模型训练工具箱中的一个基本工具。

Activation recomputation 激活重新计算 / Gradient Checkpointing

激活重计算（也称为梯度检查点 Gradient Checkpointing 或重材料化Rematerialization）的总体思路是在正向传播过程中丢弃一些激活以节省内存，并在反向传播过程中额外计算这些激活。

如果没有重新计算，我们将在两个可学习操作（例如前馈、层归一化等）之间存储每个隐藏状态，以便在反向传播中使用它们来计算梯度。

当我们使用重新计算时，通常只会在模型架构的几个关键点存储激活，丢弃其余的激活，并在反向传播过程中从最近的保存激活动态重新计算它们，基本上再次执行正向传播的一部分以交换内存和计算。它通常看起来是这样的：

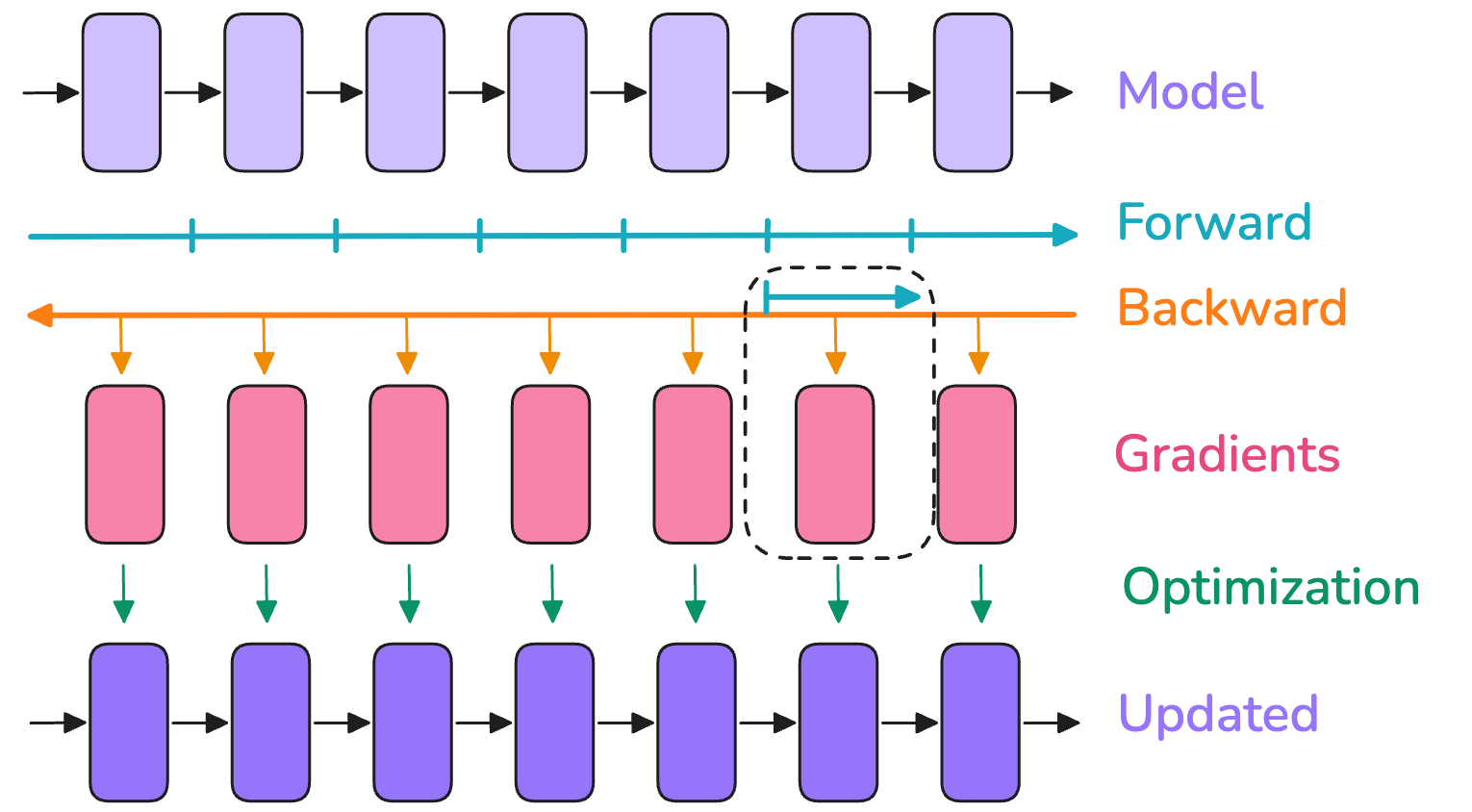
有几种策略可以选择要存储的关键激活：

  • Full: 我们在 Transformer 模型的每一层之间的过渡点检查激活。这通常被称为 full 策略，因为它需要通过每一层进行正向传递，实际上在反向传递期间增加了一个完整的正向传递。这种策略节省了最多的内存，但在计算方面是最昂贵的。它通常将计算成本和时间增加 30-40%，这是非常明显的。
  • Selective：总的来说，我们可以做得比 full 的更好。Recomputation 论文的作者对哪些部分激活占用最大且计算成本很低进行了详细分析。结果发现, 注意力计算属于这一类别，因此我们通常可以丢弃它们，并专注于检查点化昂贵的前馈计算。对于 GPT-3（175B）模型来说，这意味着在 2.7%的计算成本下，激活内存减少了 70%。

让我们看看重计算策略在实践中如何大幅减少内存占用，以及选择性重计算如何在节省内存和重计算成本之间找到一个不错的平衡点(下图左侧 使用了selective, 右侧是不使用recomputation)

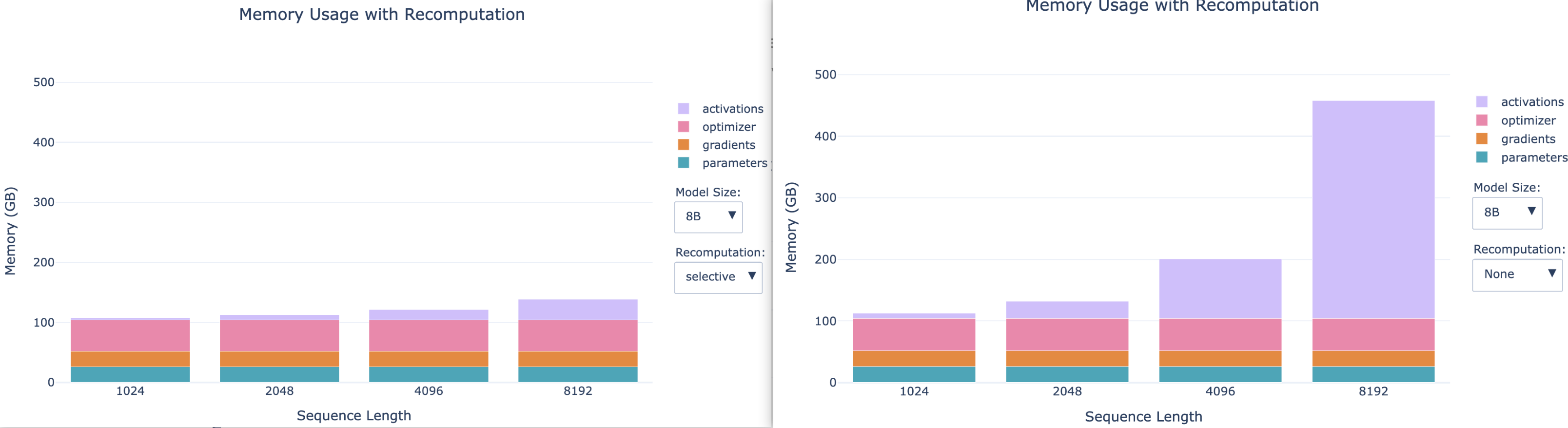
另一个明显可见的趋势是，对于较小的模型，长序列的激活作用更大，因此重新计算的效果变得更加明显。

当你测量你的训练设置使用 GPU/TPU/加速器的效率时，通常需要考虑重新计算来计算总 FLOPS（每秒浮点运算次数），并将其与 GPU/TPU/加速器的理论最大 FLOPS 进行比较。在计算训练步骤的 FLOPS 时考虑重新计算，得到一个称为“硬件 FLOPS”的值，这是在加速器上实际执行的操作数。将这个数字除以训练步骤的持续时间和最大加速器 FLOPS，得到硬件 FLOPS 利用率 （Hardware FLOPS Utilization（HFU））。

然而，最终真正重要的是在给定数据集上训练模型所需的总时间。因此，当比较各种 GPU/TPU/加速器时，如果其中之一提供了足够的内存以跳过重新计算，从而每秒执行的操作更少（较低的 HFU），但能更快地训练，那么它应该得到奖励而不是惩罚。因此，一种替代方法是计算所谓的模型 FLOPS 利用率（Model FLOPS Utilization, MFU），与 HFU 不同，它只考虑模型前向和反向传递所需的操作，不包括在测量的 FLOPs 中的重新计算。因此，这个值比训练实现更具体于模型。

大多数训练框架现在使用 FlashAttention，它通过在反向传播中重新计算注意力分数和矩阵而不是存储它们，在优化策略中本地集成激活重计算。因此，大多数使用 Flash Attention 的人已经在使用选择性重计算 (Selective Recomputation)。

如你现在所理解的那样，由于Recomputation，激活重计算会增加 FLOPs 的数量，同时显著减少内存访问开销。

这种权衡在具有小型高速内存的硬件上特别有利，如 GPU，因为访问内存通常比执行计算慢。尽管涉及额外的操作，但整体效果通常是计算更快，同时内存占用也大大降低。

现在我们了解了重新计算，我们可以像上面图表中看到的那样驯服激活内存使用！

然而，激活仍然与BS呈线性相关，上面条形图中我们所有的配置都使用了 bs=1 ，因此当我们转向更大的BS时，activation可能会再次成为一个问题。不要绝望，我们还有另一个工具——梯度累积 Gradient Accumulation来解决这个问题！

Gradient Accumulation 梯度累积

梯度累积是一种非常直接的方法来避免内存爆炸，它包括将我们的batch拆分为 Micro batch。我们将对每个Micro batch依次执行前向和反向传播，计算梯度，正如其名所示，在执行优化器步骤之前，将所有Micro batch的梯度相加。在实践中，优化步骤是在梯度平均而不是梯度总和上进行的，这样结果就与梯度累积步骤的数量无关。

将每个前向传递的batch size称为 micro batch size （mbs）。将每个优化器步骤之间的总batch size称为 global batch size （gbs）。如果为每个 8 次前向/反向传递执行一个优化器步骤，那么 global batch size 将是 micro batch size 的 8 倍。

我们现在所称的 global batch size 因此对应于我们之前为了简便而称之为 batch size 的内容（我们现在使我们的术语更加精确以避免歧义）。

使用梯度累积，全局batch size可以简单地按以下方式计算：

$$
bs=gbs=mbs\times grad_{acc}
$$

梯度累积使我们能够有效地将batch size增加到无限大（甚至更多！）同时保持内存占用不变。梯度累积还与激活重计算兼容，以进一步减少内存占用。

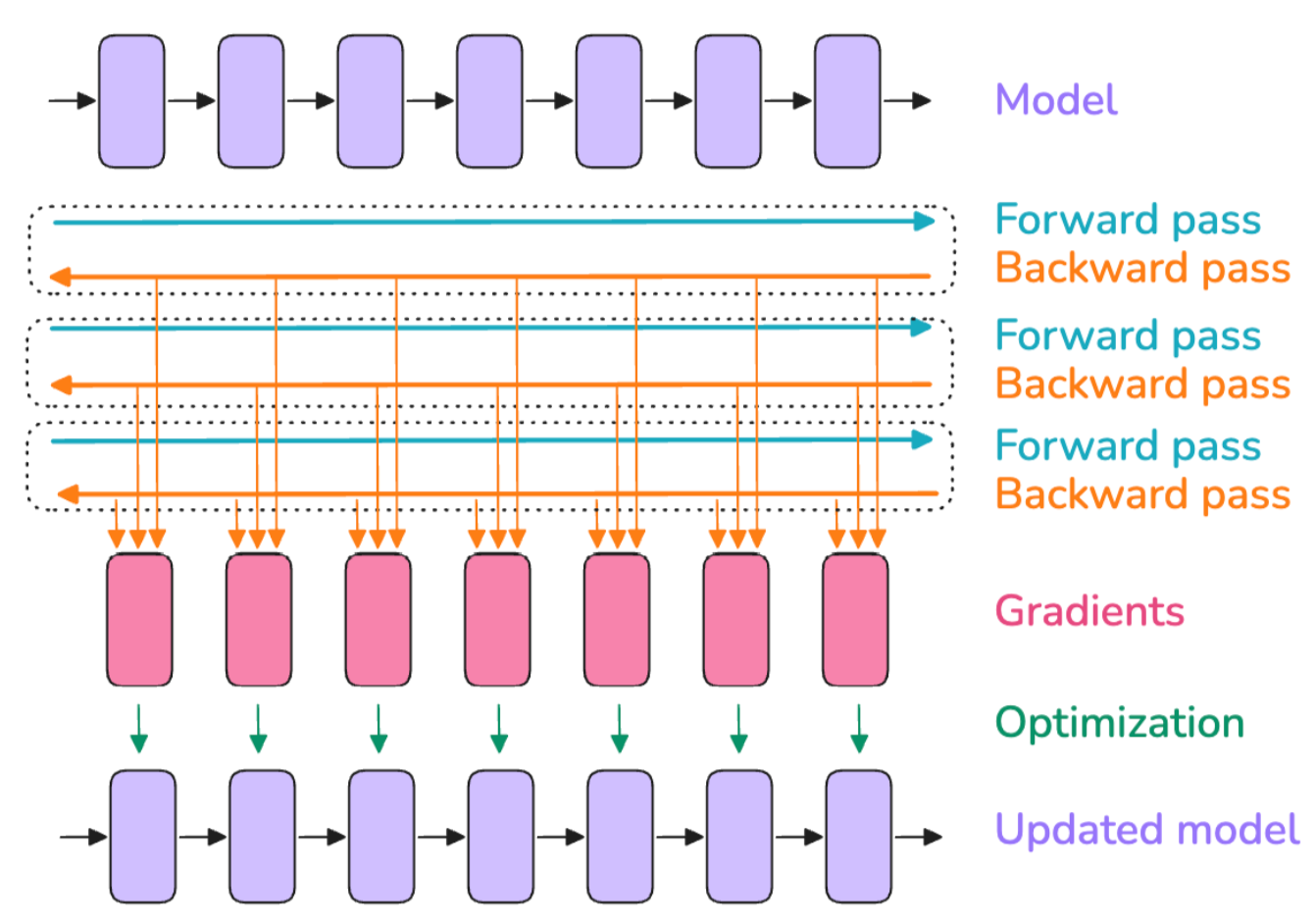
梯度累积允许我们通过仅计算部分、Micro Batch Size的激活来减少与批次大小线性增长的激活内存。

然而，一个缺点是梯度累积需要在每个优化步骤中进行多次连续的前向/反向传递，从而增加了计算开销并减慢了训练速度。No Free Lunch!

但是如果你仔细观察，你可能已经注意到每个Micro Batch的正向/反向传递实际上可以并行运行。正向/反向传递彼此独立，唯一的区别是独立的输入样本。看起来是时候开始将我们的训练扩展到多个 GPU 上了！

在之前，让我们快速浏览一下如何可视化计算和通信，并了解分布式训练工具箱中最有用的工具之一： Profiler 这个工具将非常有助于理解和验证 GPU 与计算之间的通信以及瓶颈所在。

Profiling GPU Compute and Communication 计算通信分析

PyTorch 的剖析器允许我们在训练过程中精确追踪和可视化 CPU 和 GPU 上发生的情况。它原生集成在 PyTorch 中。让我们看看如何使用它：

1
2
3
4
5
6
7
8
9
10
11
12
with torch.profiler.profile(
    activities=[
        torch.profiler.ProfilerActivity.CPU,
        torch.profiler.ProfilerActivity.CUDA,
    ],
    schedule=torch.profiler.schedule(wait=1, warmup=1, active=3),
    on_trace_ready=torch.profiler.tensorboard_trace_handler('./log/profile'),
    with_stack=True
) as prof:
    for step in range(steps):
        train_step() 
        prof.step()

这生成一个我们可以在 TensorBoard 或 Chrome 的Trace查看器中可视化的Trace。Trace中显示了：

  • CPU 线程异步启动内核到 GPU
  • 多个 CUDA 流并行处理计算和通信
  • 内核执行时间及内存分配

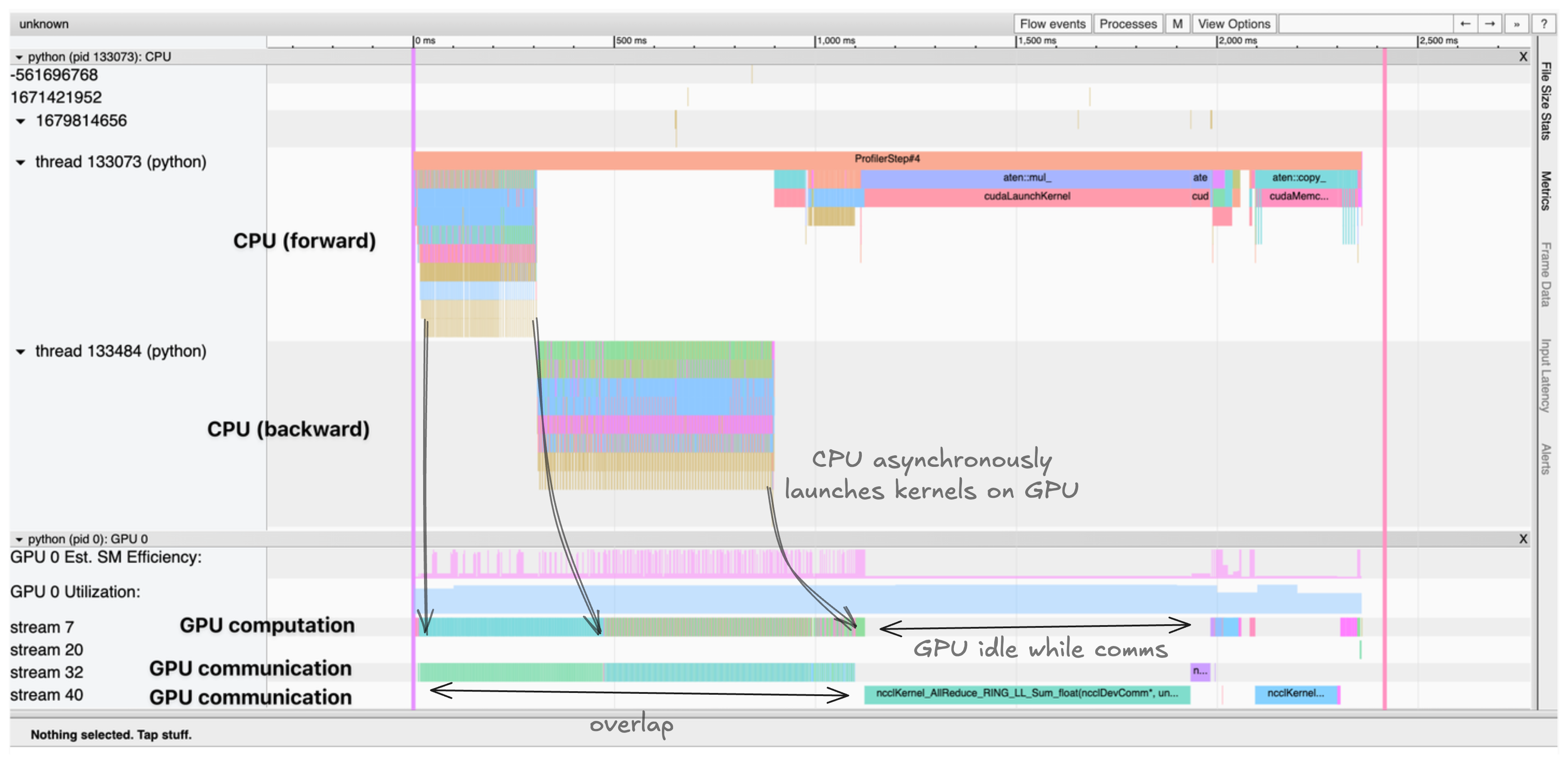
Trace显示 CPU 线程异步启动内核到 GPU，计算内核和通信在不同 CUDA 流中并行发生

追踪有助于识别瓶颈，如：

  • 顺序计算和通信可以重叠
  • 空闲 GPU 时间等待数据传输
  • CPU 与 GPU 之间的内存移动
  • CPU 启动开销

理解这些模式对于优化分布式训练性能至关重要。例如，跟踪将清楚地显示梯度同步是否与后续讨论的向后计算正确重叠。

以上是单个GPU训练相关知识，现在我们转移到多个GPU，并开始研究第一种scaling technique - 数据并行 (Data Parallel, DP)：可以视为梯度累计的并行版本。

Data Parallelism 数据并行

**数据并行（DP）**背后的思想是在多个 GPU 上复制模型（我们称复制品为“模型实例”），并对每个 GPU 上的不同Micro Batch Size数据并行执行前向和反向传播，因此得名数据并行。你可能已经在简单的训练示例中见过数据并行，但正如你很快就会看到的，我们将在本节中深入探讨，所以即使你知道一般方法，也要保持关注。

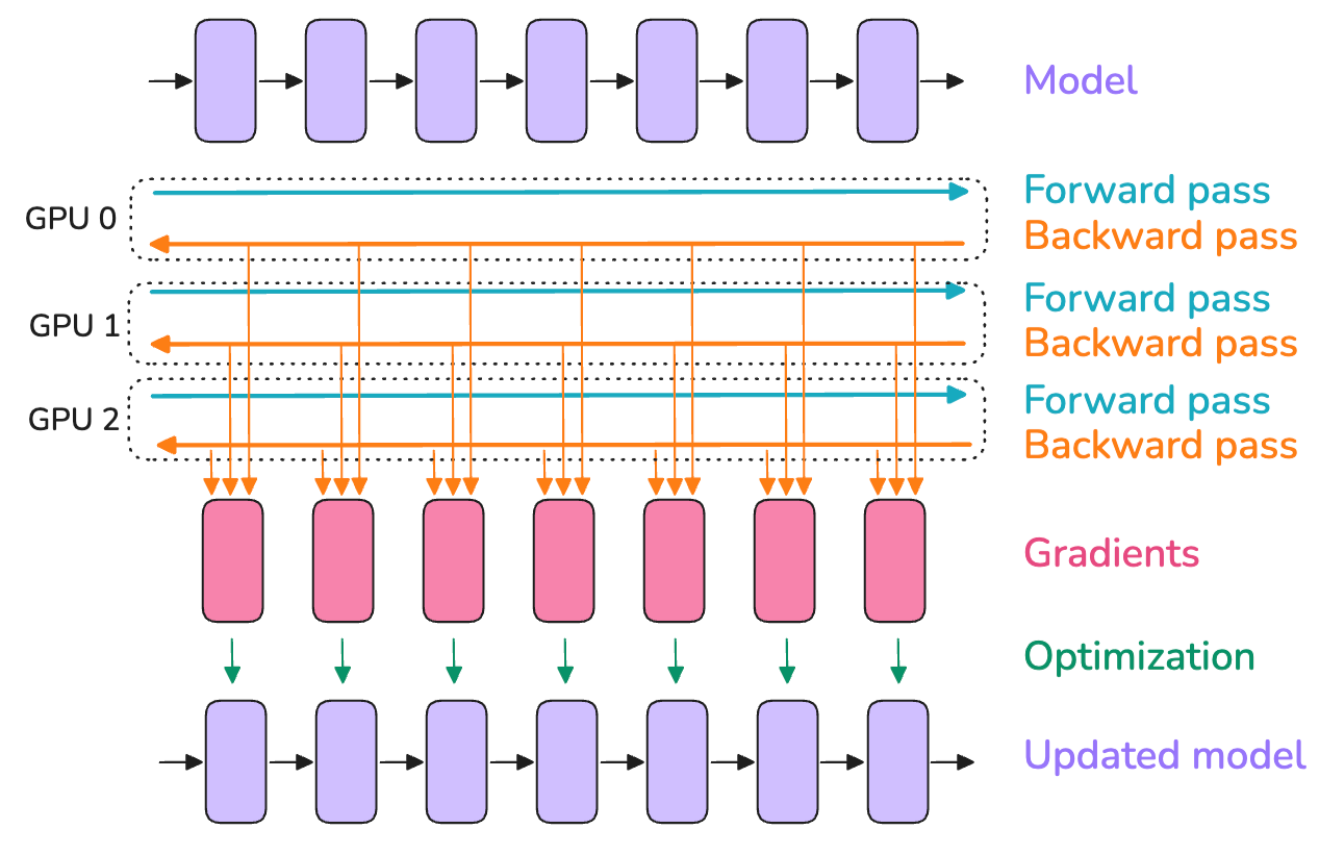
对每个GPU来说，使用不同的Micro Batch意味着每个GPU上会有不同的梯度，因此为了保持不同GPU上的模型实例同步，会在反向传播过程中，在优化器步骤之前，使用一种称为 “all-reduce” 的操作对模型实例的梯度进行平均。

这涉及到我们的第一个“分布式通信” 原语：all-reduce，用来处理 GPU 实例和节点之间的同步和通信。

一个简单的 DP 实现只会等待反向传播完成，以便我们获得所有梯度，然后触发所有 DP 进程的全量 reduce 操作，以同步这些梯度。但这样的计算顺序，随后是通信，是大忌！因为我们不希望我们的 GPU 在通信时闲置，就像上面的图中所示。

我们应尽可能尝试重叠通信和计算，以便它们尽可能同时发生。

让我们看看三种优化，这些优化使我们能够比我们最初的简单实现做得更好！

第一次优化：将梯度同步与反向传播重叠

朴素 DDP 方法的主要缺点是，在反向传播（计算）之后，必须等待梯度同步（通信）才能更新参数。能否将这种通信与我们的计算重叠？答案是肯定的！

如下图所示，层的梯度可以在计算早期层的梯度之前就进行汇总和求和。例如，一旦最后一层的反向传播完成，这些梯度就可以在反向计算继续进行早期层的同时进行汇总和求和，同时向左移动。

通过在每个参数上附加一个 all-reduce Hook 函数，在 PyTorch 中可以实现这一点。一旦该参数的梯度准备好，就会触发 all-reduce 操作，而其他参数的梯度仍在计算中。这种方法将大多数 all-reduce 操作与梯度计算重叠，从而提高了效率。以下是一个简单的附加钩子函数的示例：

1
2
3
4
5
6
7
8
def register_backward_hook(self, hook):
    """
    Registers a backward hook for all parameters of the model that 
    require gradients.
    """
    for p in self.module.parameters():
        if p.requires_grad is True:
            p.register_post_accumulate_grad_hook(hook)

重叠计算和通信可以减少等待整个模型梯度同步所需的时间。梯度同步可以（至少部分地）与反向传播并行进行，从而显著加速数据并行。以下是带有同步重叠的朴素数据并行（DP）的完整实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
class DataParallelNaive(nn.Module):
    """
    Naive Data Parallelism. Not used in practice. But it is a good starting point to understand how data parallelism works.
    It implements a simple all-reduce operation to synchronize gradients across multiple processes.
    And `no_sync` context manager to disable gradient synchronization.
    """
    def __init__(self, module):
        """
        Initializes the DataParallel wrapper for a given module.

        Args:
            module (nn.Module): The model to be wrapped for data parallelism.
            process_group (torch.distributed.ProcessGroup): The process group used for gradient synchronization. 
                                                            It could be a data parallel or context parallel group.
        """
        super().__init__()
        self.module = module
        self.require_backward_grad_sync = True # whether to synchronize gradients during backward pass. Set to False when using gradient accumulation
        self.register_backward_hook(self._allreduce_grads)
  
    def forward(self, *inputs, **kwargs):
        return self.module(*inputs, **kwargs)
  
    def register_backward_hook(self, hook):
        """
        Registers a backward hook for all parameters of the model that require gradients.  
        """
        for p in self.module.parameters():
            if p.requires_grad is True:
                p.register_hook(hook)
        
    def _allreduce_grads(self, grad):
        """
        Performs an all-reduce operation to synchronize gradients across multiple processes.  
        """
        # No synchronization needed during gradient accumulation, except at the final accumulation step.
        if self.require_backward_grad_sync:
            dist.all_reduce(grad, op=dist.ReduceOp.SUM, group=pgm.process_group_manager.cp_dp_group)
            grad /= pgm.process_group_manager.cp_dp_world_size
        return grad 
  
    @contextlib.contextmanager
    def no_sync(self):
        """
        A context manager to temporarily disable gradient synchronization. 
        This is useful for performing multiple backward passes during gradient accumulation without synchronizing 
        gradients in between.
        """
        self.require_backward_grad_sync = False
        yield
        self.require_backward_grad_sync = True

这是我们的第一个“重叠计算与通信”示例，我们将在本博客文章中多次讨论，这是实现最大扩展效率的关键技术。但我们可以进一步提高效率！

第二次优化：Bucketing Gradients 梯度分桶

GPU 操作通常在大型张量上执行比在许多小张量上执行操作更高效。这也适用于通信操作。因此，我们可以将梯度分组到桶中，并为同一桶内的所有梯度启动单个 all-reduce 操作，而不是为每个梯度执行独立的 all-reduce 操作。它通常看起来如下：

将其视为在发货前将物品装箱。发送几个大箱子比发送许多小箱子更有效率。通过为每个桶执行单个全量减少操作，我们可以显著减少通信开销并加快通信操作。

这里是一个带有分桶的代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
class DataParallelBucket(nn.Module):
    """
    Data Parallelism with gradient grouped into buckets to reduce the communication overhead.
    """
    def __init__(self, module, bucket_cap_mb=25, grad_type = torch.float32):
        """
        Initialize the DataParallelBucket module.
  
        Args:
            module (nn.Module): The model to be parallelized.
            process_group: The process group for gradient synchronization, which can be either 
                           a data parallel group or a context parallel group.
            bucket_cap_mb (int, optional): The maximum size of each gradient synchronization bucket in megabytes. 
                                           Defaults to 25 MB.
            grad_type (torch.dtype, optional): The data type of gradients, defaulting to float32.
        """
        super().__init__()
        self.module = module
        self.require_backward_grad_sync = True # whether to synchronize gradients during backward pass. Set to False when using gradient accumulation
        grad_size = 2 if grad_type == torch.bfloat16 else 4 # float32 gradient: 4 bytes
        bucket_size = bucket_cap_mb * 1024 * 1024 // grad_size # number of gradients in one bucket
        self.bucket_manager = BucketManager(module.parameters(), pgm.process_group_manager.cp_dp_group, bucket_size, grad_type)
        self.register_backward_hook()
        self._post_backward_callback_set = False # whether the callback for wait gradient synchronization is set
  
    def forward(self, *inputs, **kwargs):
        return self.module(*inputs, **kwargs)

    def backward(self, input_tensor, output_tensor, output_tensor_grad):
        return self.module.backward(input_tensor, output_tensor, output_tensor_grad)
  
    def register_backward_hook(self):
        """
        Registers a backward hook to manually accumulate and synchronize gradients.
  
        This hook serves two main purposes:
        1. PyTorch does not natively support gradient accumulation with mixed precision.
        2. After gradient accumulation, it flags parameters as ready for synchronization.
  
        The gradient accumulation functions are stored to prevent them from going out of scope.
  
        References:
        - https://github.com/NVIDIA/Megatron-LM/issues/690
        - https://pytorch.org/docs/stable/generated/torch.autograd.graph.Node.register_hook.html
        - https://arxiv.org/abs/2006.15704 (page 5)
        """
        self.grad_accs = []
        for param in self.module.parameters():
            if param.requires_grad:
                # Expand so we get access to grad_fn.
                param_tmp = param.expand_as(param)
                # Get the gradient accumulator function.
                grad_acc_fn = param_tmp.grad_fn.next_functions[0][0]
                grad_acc_fn.register_hook(self._make_param_hook(param, self.bucket_manager))
                self.grad_accs.append(grad_acc_fn)
        
    def _make_param_hook(self, param: torch.nn.Parameter,bucket_manager: BucketManager):
        """
        Creates the a hook for each parameter to handle gradient accumulation and synchronization.
        """
        def param_hook(*unused):
            """
            The hook called after the gradient is ready. It performs the following:
            1. Accumulates the gradient into the main gradient.
            2. Adds a post-backward callback to wait for gradient synchronization completion.
            3. Marks the parameter as ready for synchronization.
            """
            if param.requires_grad:
                assert param.grad is not None
                param.main_grad.add_(param.grad.data) # accumulate the gradients
                param.grad = None
        
                # skip the gradient synchronization (gradient accumulation/PP micro batches)
                if self.require_backward_grad_sync:
                    # Add a callback to wait for gradient synchronization. Ensures the callback is added only once.
                    # Callback is executed after the backward pass. It should be added per backward pass.
                    if not self._post_backward_callback_set:
                        Variable._execution_engine.queue_callback(self._post_backward)
                        self._post_backward_callback_set = True
                
                    # mark the parameter as ready for gradient synchronization. 
                    bucket_manager.mark_param_as_ready(param) 
        return param_hook
  
    @contextlib.contextmanager
    def no_sync(self):
        """A context manager to disable gradient synchronization."""
        self.require_backward_grad_sync = False
        yield
        self.require_backward_grad_sync = True
  
    def _post_backward(self):
        """
        A post-backward callback that waits for gradient synchronization to finish, then copies 
        the synchronized gradients back to the parameters' grad attribute.
  
        This method is called after the backward pass and before the optimizer step.
        """
        self.bucket_manager.wait()
        self._post_backward_callback_set = False
        # copy to params.grad so we can use the optimizer to update the parameters
        for p in self.module.parameters():
            if p.requires_grad:
                p.grad = p.main_grad.to(p.dtype) # In PyTorch, you cannot assign a gradient with one data type to a tensor of another data type.

    def reset(self):
        """
        Reset the bucket manager and zero out gradients in the model
        """
        self.bucket_manager.reset()

第三次优化：DP与梯度累计的相互作用

最后，正如我们之前所看到的，梯度累积通过在更新参数 optimizer.step() 之前执行多次前向和反向传播来实现。当将梯度累积与数据并行结合使用时，当我们想要同步梯度时，我们应该小心谨慎。

在朴素版本中，在accumulation过程中，每次反向传播后都会自动触发 all-reduce 操作，这并非最优解，因为最终步骤后的一次减少操作就能达到相同效果，同时还能减少开销。

在 PyTorch 中，这通常通过在不需要归一化的反向传播上添加 model.no_sync() 装饰器，来禁用梯度同步来解决。

在进行通信操作时，张量在内存中必须连续，以避免冗余的内存复制。为了最优地执行此操作，通常预先分配连续的缓冲区，其大小为激活或模型参数的大小，专门用于通信。虽然这可以加快通信速度，但它也部分导致了训练期间的过高的峰值内存使用。

重新审视 Global Batch Size

我们可以更新我们的batch size公式，加入我们新增加的 数据并行DP 和梯度累积参数：

$$
bs = gbs = mbs \times grad_acc \times dp
$$

  • mbs: micro batch size
  • grad_acc: 是gradient accumulation step数量
  • dp: 是并行实例数量

给定一个目标 全局batch size gbs，可以用数据并行DP过程来交换梯度累积步骤，以加快训练速度。

在实践中，人们倾向于尽可能最大化数据并行节点（DP）的数量，超过梯度累积，因为它是固有的并行，与梯度累积的顺序性质不同。然后在数据并行扩展不足以在用完 GPU 之前达到目标全局批次大小时，将梯度累积添加到数据并行之上。

DP 能够将训练分布在不同的样本上，提供了一个并行化的第一维度，从而实现了这一维度的并行性（我们将逐步涵盖另外四个维度）。

小节：关于1D parallel Training recipe:

  1. 首先应确定最佳的Global Batch Size Tokens（ GBST ），要么通过查阅文献，要么通过运行测量模型收敛性的实验。
  2. 然后选择训练的序列长度，这同样可以通过查阅文献或进行实验来实现。通常，对于我们今天进行的评估，2-8k 个标记可以可靠地工作（我们不会深入探讨训练方法，但团队通常会在训练结束时增加序列长度，混合一些更长的上下文数据样本，以达到今天的更长上下文大小）。
  3. 可以通过增加局部batch size直到内存耗尽，在单个 GPU 上找到maximum local batch size（mbs）。
  4. 最后，确定目标 DP 可用的 GPU 数量。GBS 与 DP 的比率给出了达到所需 GBS 所需的剩余梯度累积步骤数。

如果梯度累积率低于 1，即拥有过多的 GPU，也就是所谓的有钱任性，可以选择不使用所有 GPU，探索更大的全局批量大小，或者测试降低 MBS 是否会加快训练速度。在后一种情况下，我们将优先考虑吞吐量而非单个 GPU 的计算效率，使用比可能更小的 MBS 来加快训练速度。

具体举例说明：假设我们想要训练一个具有 4M 个 token 和 4k 序列长度的最新模型。因此，我们的批量大小将是 1024 个样本（选择最接近的 2 的幂）。

  • 假设我们观察到单个 GPU 只能容纳 MBS=2 的内存，并且我们有 128 个 GPU 可供训练。这意味着通过 4 个梯度累积步骤，我们将达到我们的目标，即每个训练步骤 1024 个样本或 4M 个 token。

    $gbs(1024)=128\times MBS(2)\times grad_acc(4)$

  • 现在，如果我们突然有 512 个 GPU 可用呢？我们可以通过保持 MBS=2，将梯度累积步骤设置为 1，从而实现相同的 GBS 和相同的训练，但训练速度更快！

    $gbs(1024)=512\times MBS(2) \times grad_acc(1)$

请注意，在 512+个 GPU 的规模下，根据所使用的网络，通信操作将开始受到环形延迟Ring Latency（信号在环形中传播所需的时间）的限制，这意味着不能再完全重叠 DP 通信。这将降低我们的计算效率并影响我们的吞吐量。在这种情况下，应该开始探索其他并行化的维度。

虽然数据并行DP很好地与 all-reduce 梯度同步结合，但这种好处在大规模时开始减弱。为什么？因为添加越来越多的 GPU（数百或数千个）时，它们之间的协调开销显著增加，网络需求变得过大，以至于超过了好处。因此，随着向系统中添加更多的 GPU，现有的设置将变得越来越不高效。

让我们通过一些基准来观察这一现象在实际中的应用：

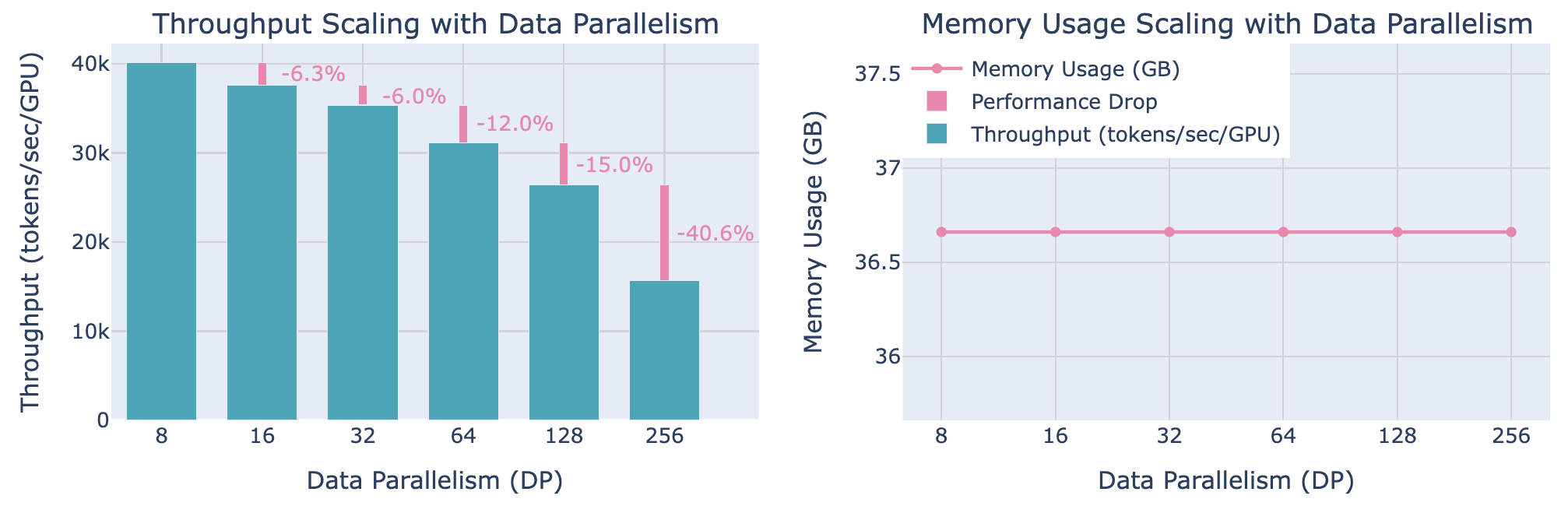
可以观察到，当超过某个限制时，吞吐量开始显著下降，而每个 GPU 的内存使用量保持恒定，并且增加更多 DP 级别不会受到影响。

数据并行是最初的简单的策略，用于在更多 GPU 上扩展训练。这种技术的工作原理类似于梯度累积，但并行化了对Micro Batch的正向和反向传递，从而提高了吞吐量！

敏锐的你可能已经注意到了，在DP的假设中，至少可以将一个输入样本的前向传递（mbs=1）放入GPU 内存中。这并不总是成立！即使是激活重新计算被激活，较大的模型也无法放入单个 GPU 中：

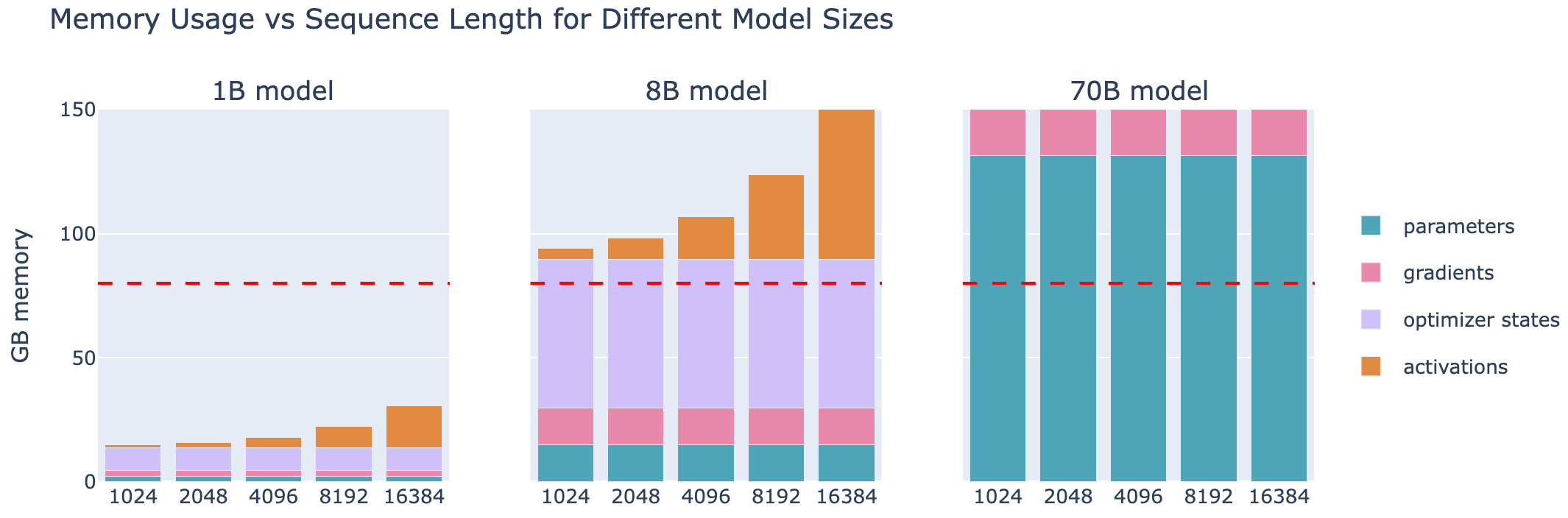
注意到，数据并行在达到一定规模后会开始出现通信开销的限制。对于这些更大的模型或更大的批量大小，我们有其他选择吗？幸运的是，确实有一些解决方案。这些方案要么是将一些张量转移到CPU上，要么是将权重、梯度以及优化器状态张量分发到多个GPU设备上！现在开始深入探讨这些方法吧。

有两种主要的分割方法：

  • 并行（Parallelism），包括张量（Tensor）、上下文（Context）或流水线（Pipeline）并行；侧重于计算加速，将计算任务分配到多个设备，缩短训练或者推理时间；
  • 共享（Sharing），例如 DeepSpeed Zero 或 PyTorch FSDP；侧重于内存优化，通过分片存储模型状态，减少每个设备的内存负担。

这两种方法在一定程度上是正交的，实际上还可以结合使用！下面将首先通过研究 ZeRO 方法来探讨它！

ZeRO (Zero Redundancy Optimizer)

本节将介绍 DeepSpeed ZeRO（零冗余优化器），这是一种旨在减少LLM训练中内存冗余的内存优化技术。

虽然数据并行是一种有效的扩展训练的方法，但将优化器状态、梯度和参数在各个 DP Rank上的简单复制引入了显著的内存冗余。ZeRO 通过在数据并行维度上划分 优化器状态、梯度和参数 来消除内存冗余，同时仍然允许使用完整的参数集进行计算。这有时需要 DP 等级之间进行更多的通信，这些通信可能或可能不会完全重叠。具体分为三个优化阶段：

  • ZeRO-1: 优化器 state partitioning
  • ZeRO-2: 优化器 state + gradient partitioning
  • ZeRO-3 (FSDP “Fully-Sharded Data Parallelism”): 优化器 state + gradient + parameter partitioning

注意到，以上并没有对激活进行分片(shard), 这是由于模型的每个 DP 副本接收不同的Micro Batch，因此每个 DP 排名上的激活也各不相同，所以它们不会被重复，因此不能进行分片！

Zero Memory使用分析

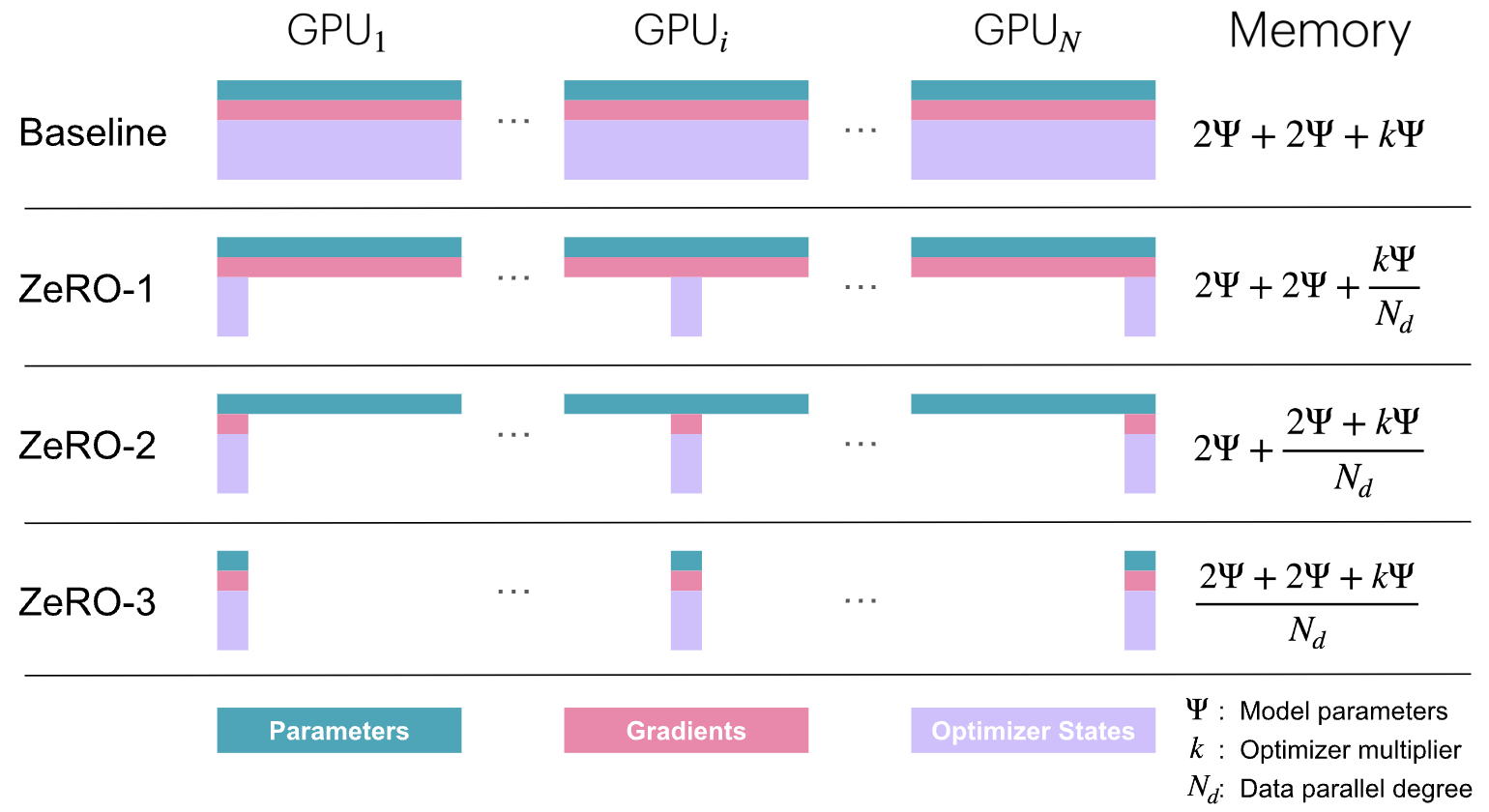
上一节中提到的在标准训练过程中优化器状态、梯度和参数的内存使用情况。让我们称我们模型的参数数量为Ψ （之前是 N，但在这里使用原始 ZeRO 论文的符号）。在混合精度训练（更多细节将在下一节中介绍）中使用 Adam 优化器时，需要存储的每个项目的内存使用情况为：

  • 模型参数 Parameter（半精度即 bf16/fp16）： 2Ψ
  • 模型梯度 Gradients（半精度即 bf16/fp16）： 2Ψ
  • 模型参数（fp32）和优化器状态： 4Ψ+(4Ψ+4Ψ)
  • 模型梯度在 fp32 中： 4Ψ （可选，仅在需要累积 fp32 梯度时计算）

如果不在 fp32 中累积梯度，这将导致总内存消耗为 2Ψ+2Ψ+12Ψ，而如果累积，将是 2Ψ+6Ψ+12Ψ。为了简化，我们先关注不使用 fp32 梯度累积的情况，但你只需将受 ZeRO-2 和 3 影响的额外字节添加到梯度项中即可。

ZeRO 的理念是将这些对象在 DP Rank 的各个进程中分片Shard，每个节点只存储一部分，当需要时再重建，从而按数据并行度将内存使用量分成 $N_d$ （DP degree)

Zero-1: 分区 优化器状态

在标准 DP 中，所有Rank在反向传播后收集相同的梯度并同时执行相同的优化步骤。这似乎是很多重复的工作。能否避免它同时减少内存使用？

在 ZeRO-1 中，优化器状态被划分为 $N_d$ 个相等的部分，其中 $N_d$  是 DP degree。这意味着每个模型副本在每个 DP 排名上只跟踪优化器状态的 $1/N_d$  。在优化步骤中，只有  $1/N_d$ 的 float32 权重被更新。

然而，在正向传播过程中，每个副本都需要所有参，因此我们需要在优化器步骤之后添加一个额外的 all-gather 操作（这是我们遇到的第二种集合通信原语！）以确保每个模型副本都有完整的最新权重。

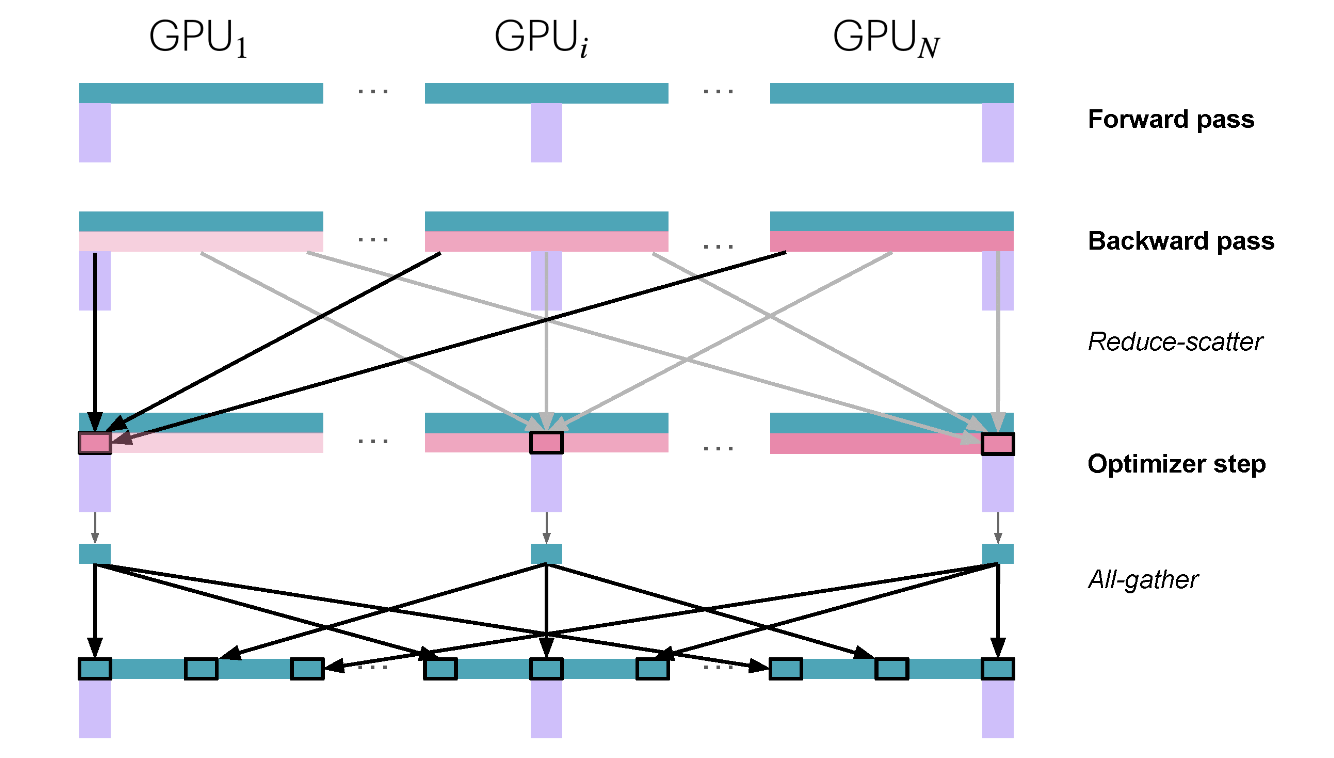
这解释了我们在上面图表中看到的 $2\Psi + 2\Psi + \frac{k\Psi}{N_d}$ 的内存公式！以下是单个训练步骤的操作序列摘要

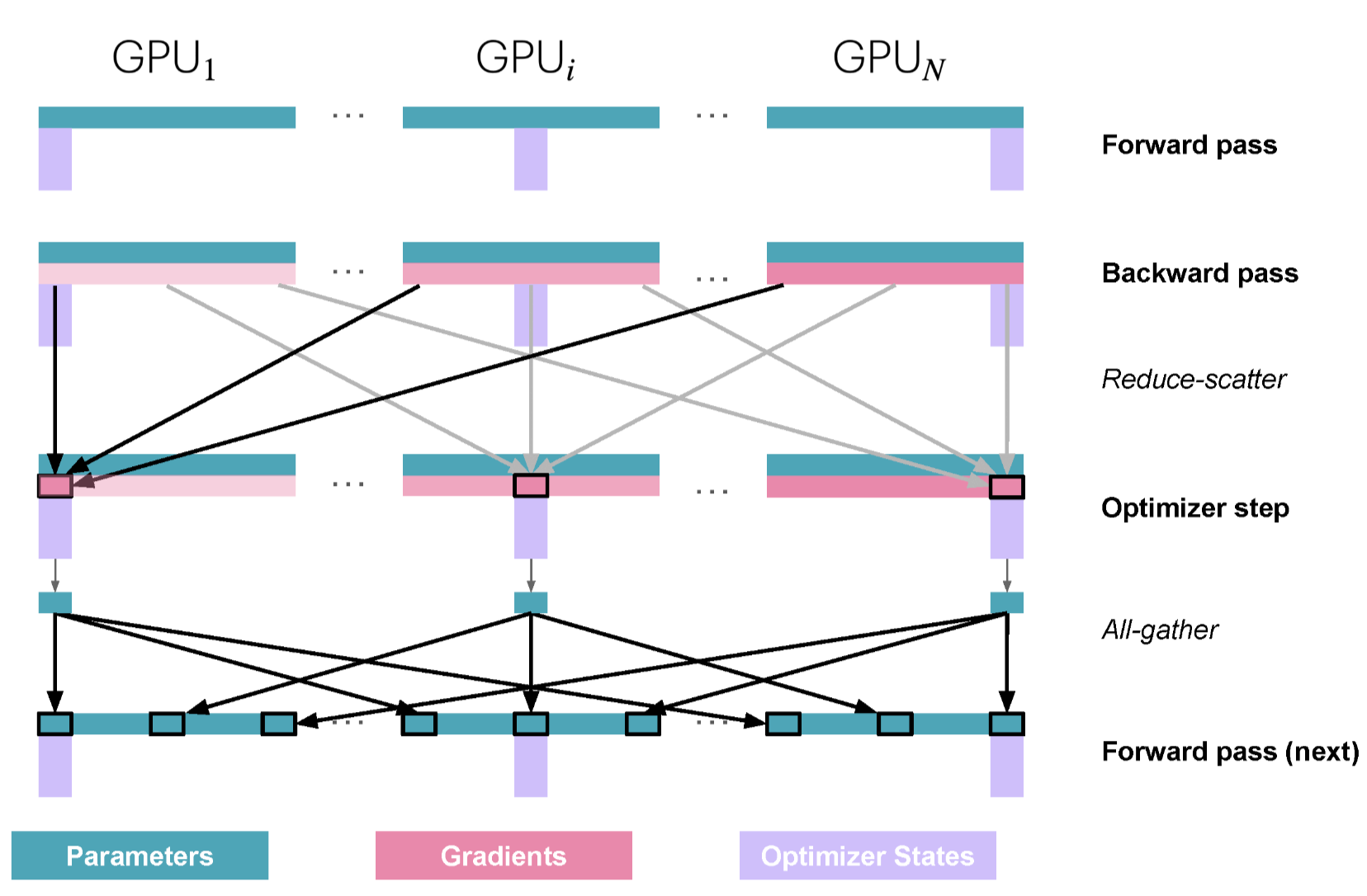
  • 前向传播，使用每个副本相同的完整 bf16 参数集，但副本间的Micro Batch Size不同
  • 反向传播，每个副本使用相同的完整梯度集，但副本间的Micro Batch Size不同
  • 对梯度执行 reduce-scatter 操作（我们将在下面的图中解释 reduce-scatter 原语）
  • 每个副本在其本地优化器步骤上执行一个优化器步骤（仅限于 $\frac{1}{N_d}$ 优化器状态），以获取更新的 $\frac{1}{N_d}$ fp32 参数，这些参数随后可以转换为 $\frac{1}{N_d}$完整 bf16 参数集。
  • 执行 bf16 参数的 all-gather 操作，将缺失的切片发送回每个副本。这是 ZeRO 中的新操作，在 vanilla DP 中未使用。

Reduce-Scatter: 结合了归约（Reduction）和分发（Scatter）两个步骤，用于在多个进程或节点之间对数据进行计算并分发结果(如下图所示）。

  • 归约（Reduction）：将多个进程的数据按照某种操作（如求和、求最大值、求最小值等）合并成一个结果。
  • 分发（Scatter）：将结果分割并分发到各个进程，使得每个进程接收一部分数据。
  • Reduce-Scatter 把这两个操作组合起来：先对所有进程的数据进行归约，然后将归约后的结果分发到各个进程。

All-Gather: 目标是收集所有进程的数据，并将这些数据分发给每个进程，使得每个进程最终拥有所有进程的完整数据副本:

  • Gather（收集）：将多个进程的数据集中到某个地方。
  • All：表示不仅收集数据，还要将收集到的完整数据广播给所有进程。
  • All-Gather 的本质是：每个进程贡献自己的数据，所有进程最终获得所有数据的组合。

在通信方面，与标准 DP 相比，Zero-1 将 all-reduce 梯度通信改为 reduce-scatter 操作，并在优化器步骤之后对所有参数执行 all-gather 操作。如下所示：

在之前章节中，介绍了vanilla DP 中可以将 all-reduce 梯度通信与反向传播计算重叠。在 ZeRO-1中，我们还可以研究如何高效地重叠新添加的 bf16 参数的 all-gather 。这里有两大策略：

  • 在优化器步骤中：可以在优化器更新部分参数后立即启动 all-gather 。这允许通信可能与其他参数更新重叠。
  • 在正向传播过程中：可以将每一层参数的 all-gather 与正向传播过程重叠。

Zero-2: Add Gradient Partitioning

由于只需要在每个副本上拥有与优化器状态块对应的梯度块，因此将梯度也像优化器状态一样分块是有意义的。在反向传播过程中，我们不是对梯度执行 all-reduce ，而是只执行 reduce-scatter 操作！在这里，只将显存中需要的 $\frac{1}{N_d}$的梯度进行 scatter，从而比 ZeRO-1 节省更多内存。

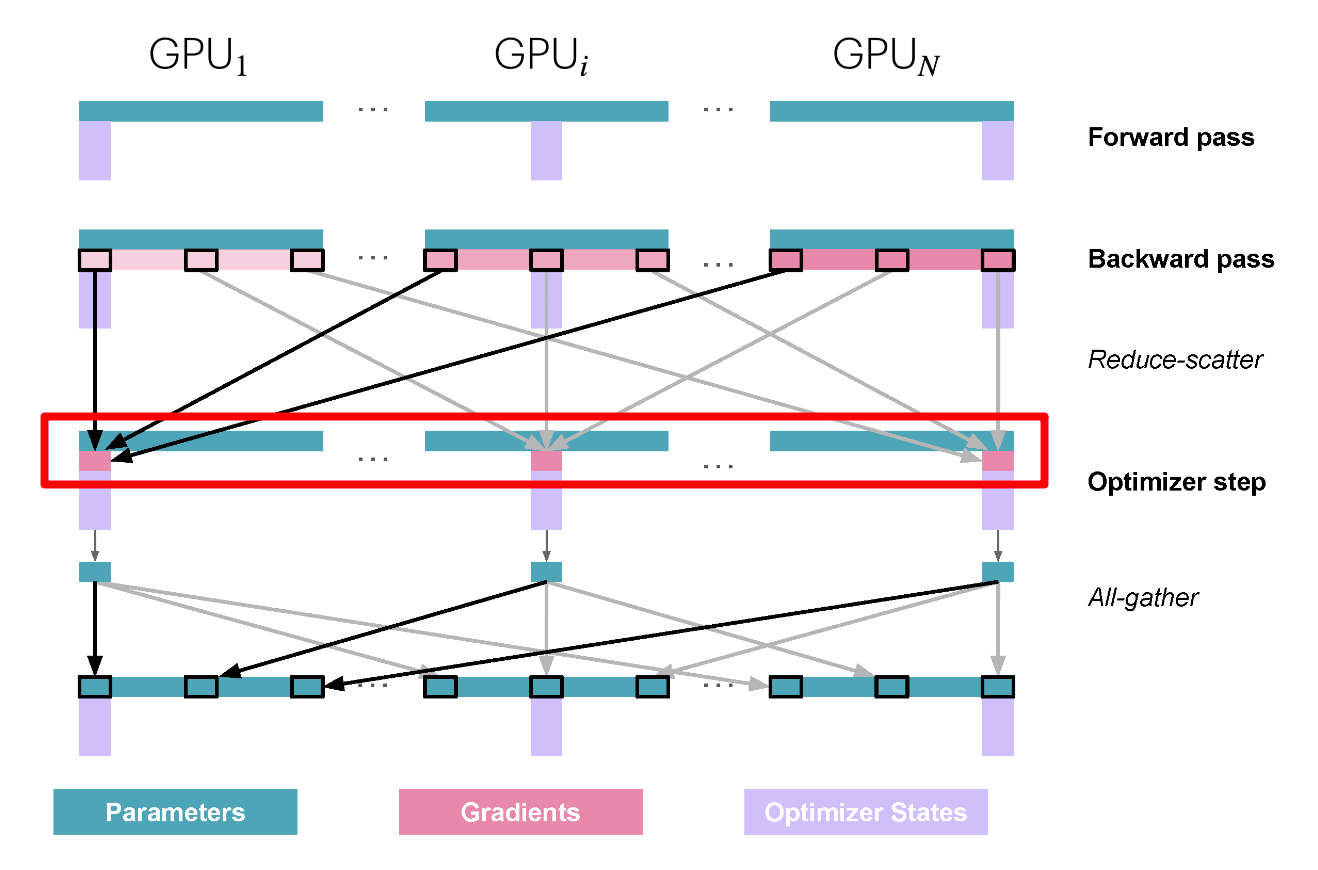
现在很容易看出，梯度分片导致 $2\Psi + \frac{2\Psi + k\Psi}{N_d}$ ，随着 $N_d$ 的增加，我们可以节省高达 8 倍的Gradient和Optimizer State显存占用。在通信方面，与 ZeRO-1 相同的过程适用，唯一的区别是Zero-2边通信边释放。因此，ZeRO-2 在通信方面也与 vanilla DP 训练相当。

在通信方面，ZeRO-2 与 ZeRO-1 相似，它们都需要对梯度进行 reduce-scatter 操作，并对所有参数进行 all-gather 操作。

相比Zero-1, Zero-2完全没有任何开销，所以Zero-2是更有选择；

相比Zero-1, Zero-2完全没有任何开销，所以Zero-2是更有选择；

Zero-3: 添加 Parameter Partitioning

对于第三阶段，我们扩展了上述在 DP 副本上对优化器状态和梯度进行分片的方法，直至对模型参数进行分片。

这个阶段也被称为 PyTorch 原生实现中的 FSDP（完全共享数据并行）。在这篇博客文章中，我们只提到 ZeRO-3，但你可以理解为 FSDP。

所以，如果模型的所有部分都是分布式的，我们如何在实践中进行正向或反向传播？很简单，当我们需要时，我们会按需收集它们。在正向传播中，这看起来如下：

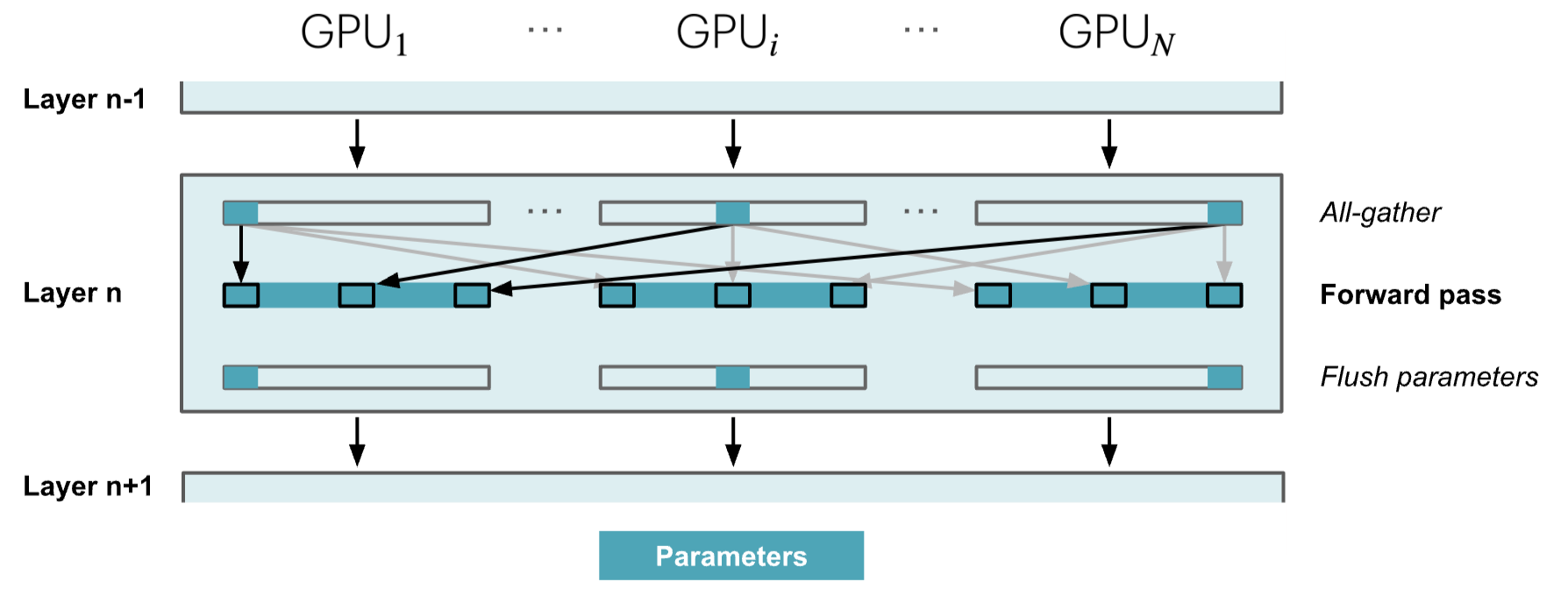
因此，当执行正向传播并按顺序遍历层时，我们会按需检索必要的参数，并在不再需要它们时立即从内存中清除。反向传播的工作方式相同，只是流程相反，我们生成梯度碎片：

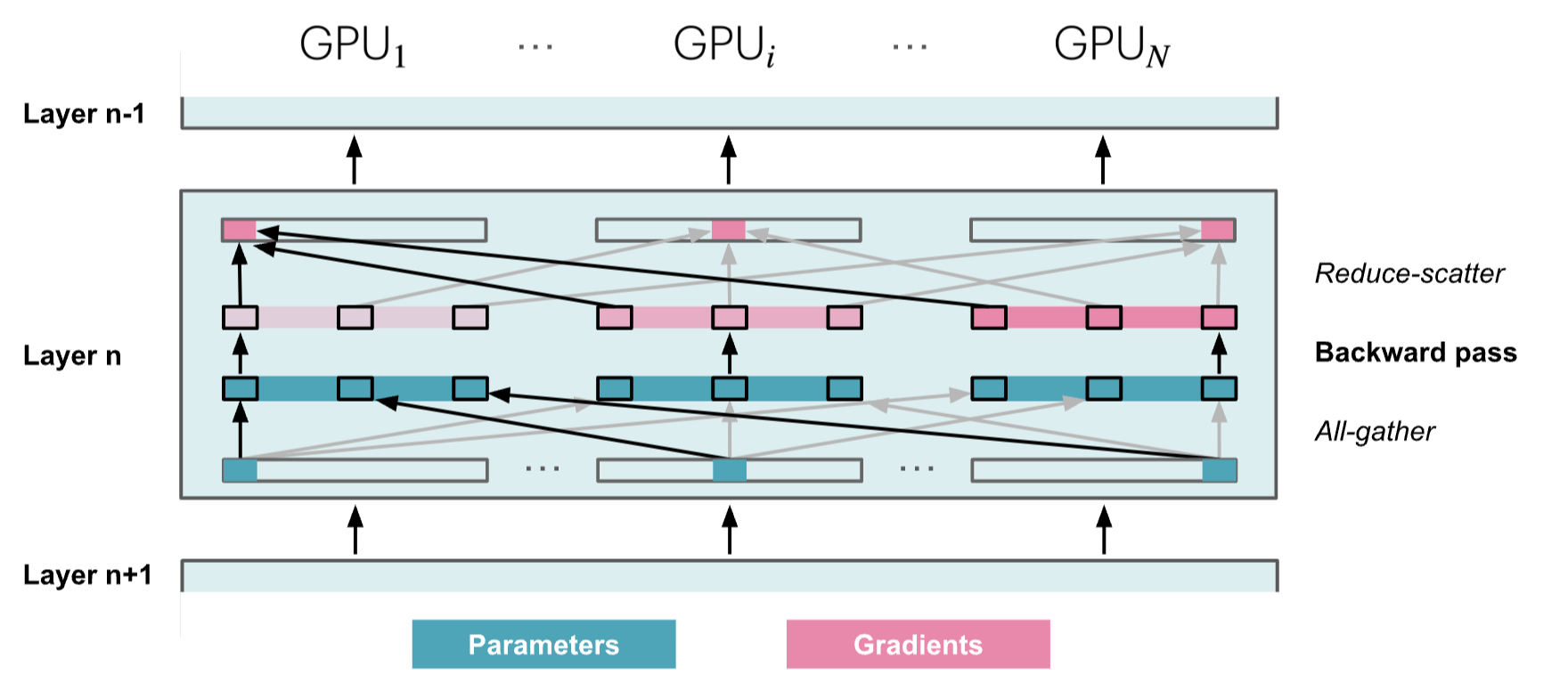
其他问题是，我们需要在正向和反向步骤中持续进行所有聚集，这相当于在训练步骤中比 Zero-2 多出 2⋅num_layers−1 次 all-gathers，每次都伴随着我们可以在下图中看到的小型基础延迟开销

在正向传播过程中，我们需要参数时进行 all-gather 操作，因此产生一个Ψ 通信成本。由于我们在正向传播中使用参数后立即丢弃它们，因此在反向传播过程中也需要进行一次额外的 all-gather 从而产生另一个Ψ 通信成本。最后需要与 ZeRO-2 中相同的 reduce-scatter 操作来处理梯度，这也需要Ψ 通信成本，从而使总通信成本达到3Ψ 。而 Zero-2 的通信成本为2Ψ 。

这可能听起来通信开销很大，但实际上可以接受，因为可以在所谓的预取 prefetching 中重叠下一层的参数通信与当前层的正向传播。在预取中，我们在正向传播中对层 n+1 进行 all-gather 权重，同时进行层 n 的正向传播，同样，我们在反向传播层 n 时对层 n-1 进行 all-gather 权重。当然，这种重叠只有在我们没有过度 scale DP 的情况下才成立。（一般来说，DP 不应超过 512）

预取（Prefetching）：在当前计算任务完成之前，提前发起通信或加载下一批数据/参数到内存或缓存中。隐藏延迟：通过将通信操作与计算操作重叠（Overlap），避免通信成为瓶颈。典型场景：
• 在分布式深度学习中，Prefetching 常用于在 GPU 计算当前批次梯度时，提前从其他设备或主机加载下一批数据的梯度或参数。
• 在数据并行中，Prefetching 可以提前发起 All-Reduce 或 Reduce-Scatter 操作，减少等待时间。

  • 预取（Prefetching）：在当前计算任务完成之前，提前发起通信或加载下一批数据/参数到内存或缓存中。
  • 隐藏延迟：通过将通信操作与计算操作重叠（Overlap），避免通信成为瓶颈。
  • 典型场景：
  • 在分布式深度学习中，Prefetching 常用于在 GPU 计算当前批次梯度时，提前从其他设备或主机加载下一批数据的梯度或参数。
  • 在数据并行中，Prefetching 可以提前发起 All-Reduce 或 Reduce-Scatter 操作，减少等待时间。

在内存方面，我们可以看到我们的方程现在达到了最终形式

$$
\frac{2\Psi + 2\Psi + k\Psi}{N_d}
$$

这意味着如果我们能提高 DP Rank $N_d$，就可以无限期地降低内存使用。注意，这对中间层激活没有帮助，对于这一点，我们可以使用我们在前几章中看到的激活检查点 Activation Checkpointing 和梯度累积 Gradient Accumulation。

总结一下到目前为止对 DP 和 ZeRO 的探索：我们看到了通过 DP，可以通过简单地通过添加更多模型副本来扩展训练，从而显著提高训练吞吐量。使用 ZeRO，可以通过在 DP 上分片参数、梯度和优化器状态，训练那些通常无法适应单个 GPU 的模型，同时产生较小的通信成本。

然而，这里有一个限制，DP 仅在模型的一层适合单个 GPU 时才起作用，ZeRO 只能划分参数、梯度和优化器状态，但不能划分激活内存！激活内存与序列长度和batch size成比例。本可以设置这些参数来限制这些，但在实践中，我们不想因为硬件限制而只能使用短序列长度进行训练。

下图展示的是8B模型的Memory Usage，当seq length很长的时候，Activation将主导内存占用；

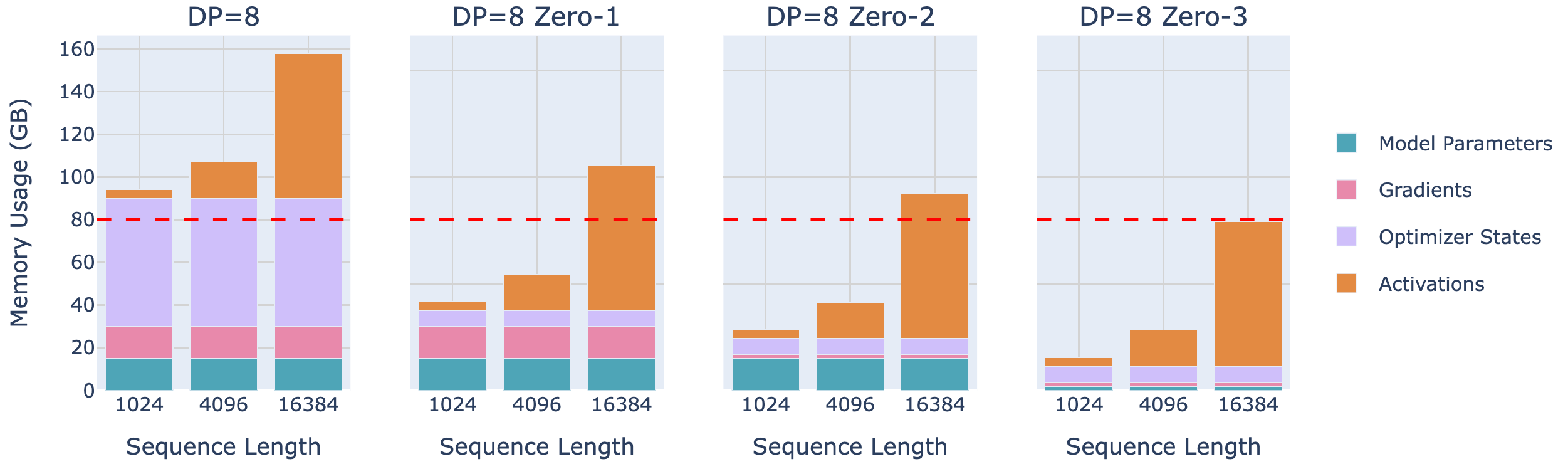
为了克服这些问题，是时候探索一个新的、正交的策略——张量并行（Tensor Parallel, TP）。与依赖于大量参数通信的 ZeRO3 不同，TP 提出将参数、梯度、优化器状态以及激活在设备间进行分片，而不需要在 GPU 之间进行任何模型参数的通信。

Tensor Parallel 张量并行

目前使用 ZeRO 对模型的参数、梯度和优化器状态进行了分片，但一旦激活Activation 内存超过内存预算，就遇到了瓶颈。

而 Tensor Parallelism（TP）方法 不仅对权重、梯度和优化器状态进行分片，还对激活进行分片，而且无需在计算前收集它们。让我们首先看看 Tensor Parallel 是如何与简单的矩阵乘法一起工作的。

张量并行利用矩阵乘法的数学特性 $A\times B$, 让我们考察两个使这种并行化成为可能的基本方程：

$$
A \cdot B = A \cdot \begin{bmatrix} B_1 & B_2 & \cdots \end{bmatrix} = \begin{bmatrix} AB_1 & AB_2 & \cdots \end{bmatrix} \
A \cdot B = \begin{bmatrix} A_1 & A_2 & \cdots \end{bmatrix} \begin{bmatrix} B_1 \ B_2 \ \vdots \end{bmatrix} = \sum_{i=1}^{n} A_i B_i
$$

这意味着我们可以通过以下两种方式之一计算矩阵乘积：1) 分别乘以B的每一列；2) 分别乘以每一行并将结果组合。在神经网络中，矩阵乘积通常以以下格式表示：X×W，其中 X 代表输入或者激活；W代表nn.Linear的权重矩阵；举例如下：

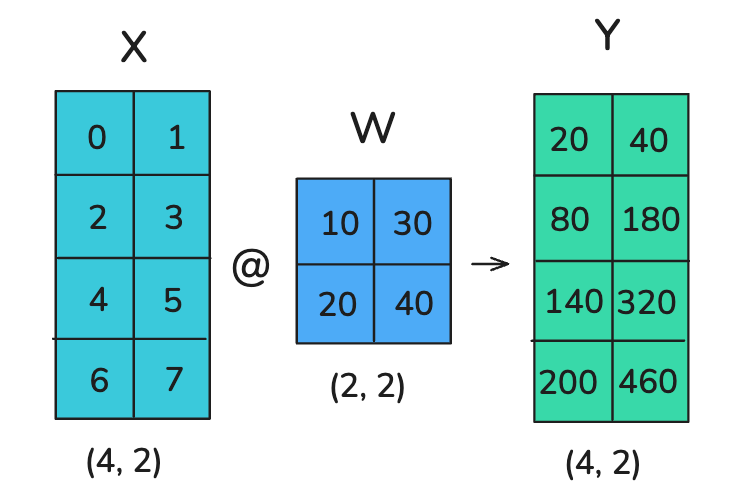
让我们看看如何并行化这个操作！在张量并行中，张量将沿着特定维度分成 N 个碎片，并分布在 N 个 GPU 上。矩阵可以在列部分或行部分进行分割，从而实现行和列并行。在接下来的内容中，我们会看到选择行或列碎片化将需要不同的通信原语。

第一个选项是使用按照列进行分片（也称为 Column-linear ）：完整输入矩阵复制到每个工作节点，需要执行 broadcast 操作，并将权重矩阵拆分为列。然后，输入与部分权重矩阵相乘，最后使用 all-gather 操作合并结果。

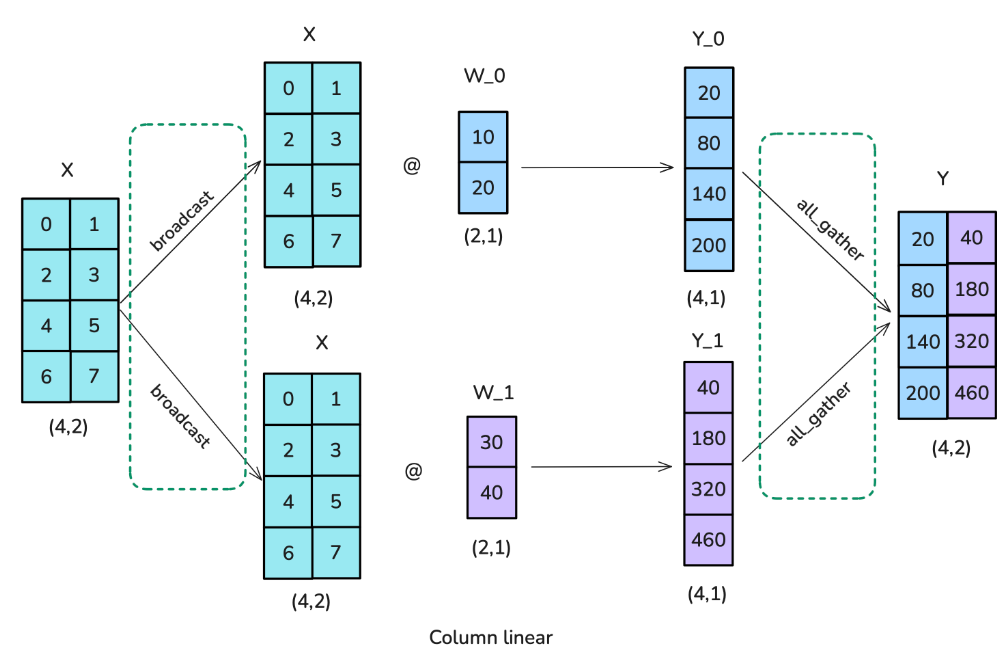
代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
class ColumnParallelLinear(torch.nn.Module):
    """Column Parallel Linear layer
    Y = XW + b, where weight matrix W is parallelized along its second dimension. W = [W_1, ..., W_p]
    This module returns the results of Y_i = XW_i + b_i in the forward method, Y_i is parallelized in the second dimension.
    Arguments:
        in_features: first dimension of weight matrix W.
        out_features: second dimension of weight matrix W.
        bias: If true, add bias
        init_method: method to initialize weights
        gather_output: If true, gather the output from all the partitions. This is used for the last linear layer
    """

    def __init__(
        self,
        in_features: int,
        out_features: int,
        bias: bool = False,
        gather_output: bool = False,
        async_all_reduce: bool = False,
    ) -> None:
        super(ColumnParallelLinear, self).__init__()

        self.tp_world_size = pgm.process_group_manager.tp_world_size
        self.tp_rank = pgm.process_group_manager.tp_rank 

        self.in_features = in_features
        self.out_features = out_features
        assert out_features % self.tp_world_size == 0, "Hidden dimension must be divisible by the tensor parallel world size"
        self.output_size_per_partition = out_features // self.tp_world_size
        self.gather_output = gather_output
        self.async_all_reduce = async_all_reduce
        # Allocate space for the weight and bias
        # Note: torch.nn.functional.linear performs XW^T + b so we exchange the order of dimensions
        self.weight = nn.Parameter(torch.Tensor(self.output_size_per_partition, self.in_features)) # W_i
        if bias:
            self.bias = nn.Parameter(torch.Tensor(self.output_size_per_partition))
            with torch.no_grad():
                self.bias.zero_()
        else:
            self.register_parameter("bias", None)

        self.reset_parameters()

    def reset_parameters(self):
        # Initialize weight tensor with the default initialization
        # method used for nn.Linear in PyTorch
        master_weight = torch.empty(
            self.out_features, 
            self.in_features, 
            dtype=self.weight.dtype,
            device=self.weight.device,
            requires_grad=False
        )
  
        # Calculate bound based on master weight's input dimension
        k = 1 / master_weight.size(1)
        bound = math.sqrt(k)
        torch.nn.init.uniform_(master_weight, -bound, bound)
        # 这里随机初始化权重，模拟主权重
  
        # Split the model into size of self.output_size_per_partition
        # 这里执行对weight的分片
        weight_list = torch.split(master_weight, self.output_size_per_partition, dim=0)
        # 根据TP Rank访问对应切片
        self.weight.data = weight_list[self.tp_rank].contiguous()
  
    def forward(self, x: torch.Tensor) -> torch.Tensor:  
        if self.async_all_reduce:
            output = linear_with_async_all_reduce(x, self.weight, self.bias) 
        else:
            output = linear_with_all_reduce(x, self.weight, self.bias) 
        if self.gather_output:
          # 这里执行all gather 
            output = GatherFromModelParallelRegion.apply(output)
        return output

解释：

  1. Input 的 broadcast：
  • 隐含在 forward 中假设 x 已广播到所有进程。这是列并行设计的标准假设
  1. 对 W 进行分片：
  • 在 reset_parameters 中，通过 torch.split(master_weight, self.output_size_per_partition, dim=0) 将权重按列分割，并根据 tp_rank 分配。
  1. All-gather：
  • 在 forward 中，当 self.gather_output == True 时，通过 GatherFromModelParallelRegion.apply(output) 收集所有进程的输出。

第二种方案被称为行分片（也称为 row-linear )：行线性分片意味着将权重矩阵分成行块。然而，这也需要将输入进行分割，这需要一个 scatter 操作，而不是像 column-linear sharding 那样使用广播操作。每个工作节点的结果已经处于正确的形状，但需要求和以得到最终结果，因此在这种情况下需要 all-reduce 操作。

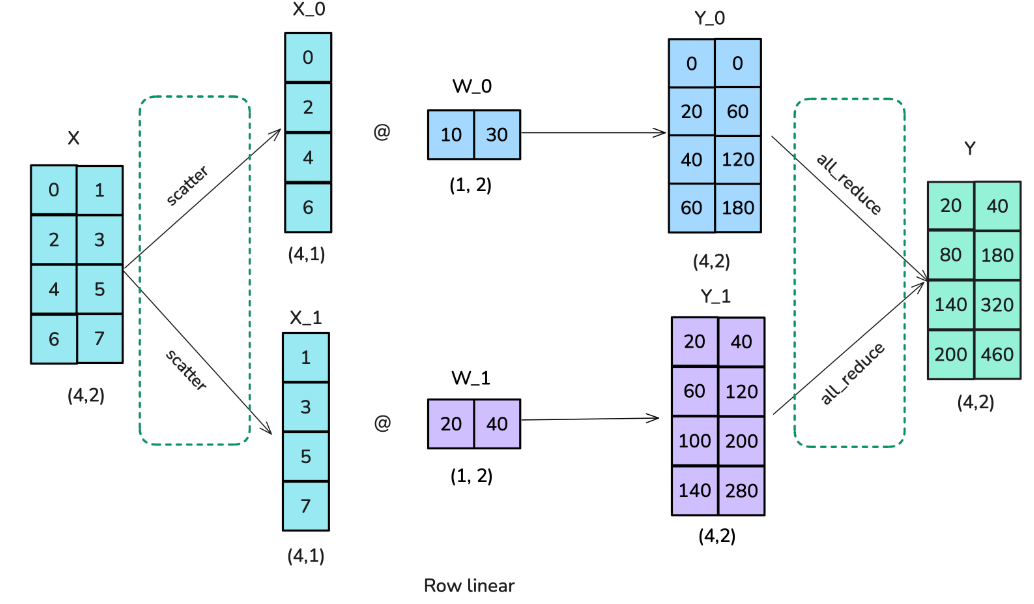
以下是行向张量并行的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69

class RowParallelLinear(nn.Module):
    """Linear layer with row parallelism.
    Y = XW + b. W is parallelized along its first dimension and X along its second dimension as:
               -   -
              | W_1 |
              | .   |
          W = | .   |        X = [X_1, ..., X_p]
              | .   |
              | W_p |
               -   -
    We assume that X is already parallelized. This is the case after ColumnParallelLinear.
    This module returns the results of Y = sum(X_i * W_i + b_i) in the forward method.
    Arguments:
        in_features: first dimension of matrix W.
        out_features: second dimension of matrix W.
        bias: If true, add bias
        init_method: method to initialize weights.
    """
    def __init__(self, in_features: int, out_features: int, bias: bool):
        super(RowParallelLinear, self).__init__()

        self.tp_world_size = pgm.process_group_manager.tp_world_size
        self.tp_rank = pgm.process_group_manager.tp_rank 

        self.in_features = in_features
        self.out_features = out_features
        assert in_features % self.tp_world_size == 0, "Hidden dimension must be divisible by the tensor parallel world size"
        self.input_size_per_partition = in_features // self.tp_world_size

        self.weight = nn.Parameter(torch.Tensor(self.out_features, self.input_size_per_partition))
        if bias:
            self.bias = nn.Parameter(torch.Tensor(self.out_features))
            # Always initialize bias to zero.
            with torch.no_grad():
                self.bias.zero_()
        else:
            self.register_parameter("bias", None)

        self.reset_parameters()

    def reset_parameters(self):
        # Initialize weight tensor with same dtype and device as self.weight
        master_weight = torch.empty(
            self.out_features, 
            self.in_features, 
            dtype=self.weight.dtype,
            device=self.weight.device,
            requires_grad=False
        )
  
        # Calculate bound based on master weight's input dimension
        k = 1 / master_weight.size(1)
        bound = math.sqrt(k)  
        torch.nn.init.uniform_(master_weight, -bound, bound)
  
        # Split the model into size of self.input_size_per_partition
        weight_list = torch.split(master_weight, self.input_size_per_partition, dim=1)
        # 在这里切分weight，分为TP rank份
        self.weight.data = weight_list[self.tp_rank].contiguous()

    def forward(self, x):
        # X_i * W_i^T + b
        output_parallel = F.linear(x, self.weight)
        # All-reduce across all the partitions.
        # 执行all-reduce 
        output = ReduceFromModelParallelRegion.apply(output_parallel)
        return output if self.bias is None else output + self.bias

解释：

  • 对 W 进行分片：
  • 在 reset_parameters 中，通过 torch.split(master_weight, self.input_size_per_partition, dim=1) 将权重按行分割，并根据 tp_rank 分配。
  • All-reduce：
  • 在 forward 中，通过 ReduceFromModelParallelRegion.apply(output_parallel) 将每个进程的局部输出 X_i * W_i^T 求和，生成完整的 Y。

Transformer 块中的张量并行

为了制定一个策略，让我们从Toy Example 示例过渡到真实模型构建块。Transformer 模型由两个主要构建块组成：前馈层（MLP）和多头注意力（MHA）。我们可以将张量并行应用于两者。

前馈部分可以通过先进行 “Column Linear” 操作，然后进行 "Row Linear" 操作来实现并行化，这相当于广播以复制输入，并在正向传播中进行 all-reduce 。

请注意，在实际训练中不需要广播，因为已经确保输入在 TP ranks 之间已经同步。这种设置比先进行 Row-Linear 操作，然后进行 Column-Linear 操作更高效，因为我们可以在两个分割操作之间跳过中间的 all-reduce 。

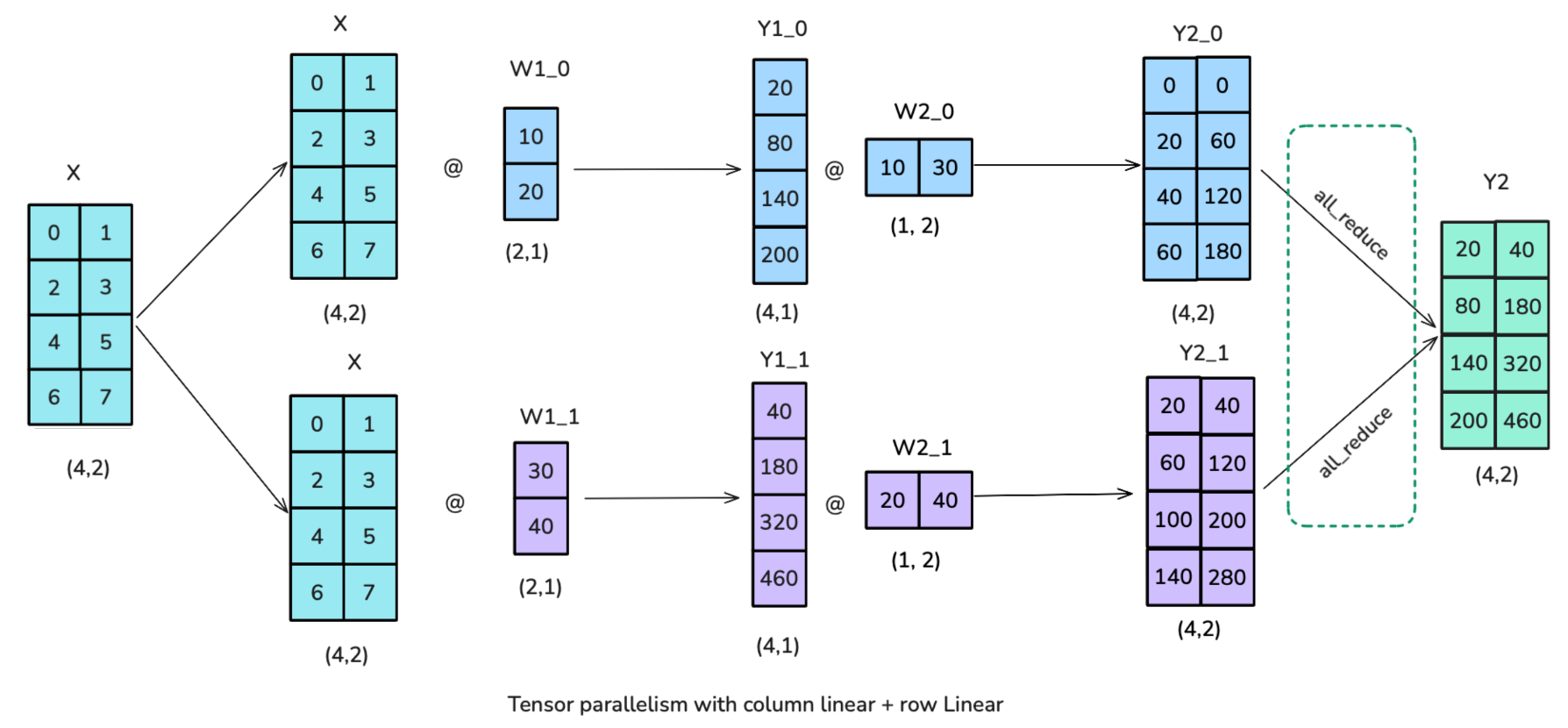
可以从以上示意图中观察到，column linear的输出刚好符合row linear的输入要求，因此可以不进行 al-reduce，可以节省了通信。

现在我们已经找到了 Transformer FeedForward 部分的效率方案，让我们来看看多头注意力块（MHA）。

我们可以一般遵循类似的方法，其中 Q、K 和 V 矩阵以 列并行方式分割，输出投影沿行维度分割。在多头注意力中，列并行方法有非常自然的解释：每个worker计算单个或一组头部的注意力。同样的方法也适用于多查询（MQA）或分组查询注意力（GQA），其中键和值在查询之间共享。

注意

  • 张量并行度不应超过 Q/K/V 头数，因为我们需要每个 TP Rank的完整头（否则无法独立在每个 GPU 上计算注意力，需要额外的通信操作）。
  • 如果使用 GQA，TP 度实际上应该小于 K/V 头数。例如，LLaMA-3 8B 有 8 个K/V 头，因此张量并行度应不超过 8。
  • 如果为这个模型使用 TP=16，我们需要在每个 GPU 上复制 K/V 头，并确保它们保持同步。

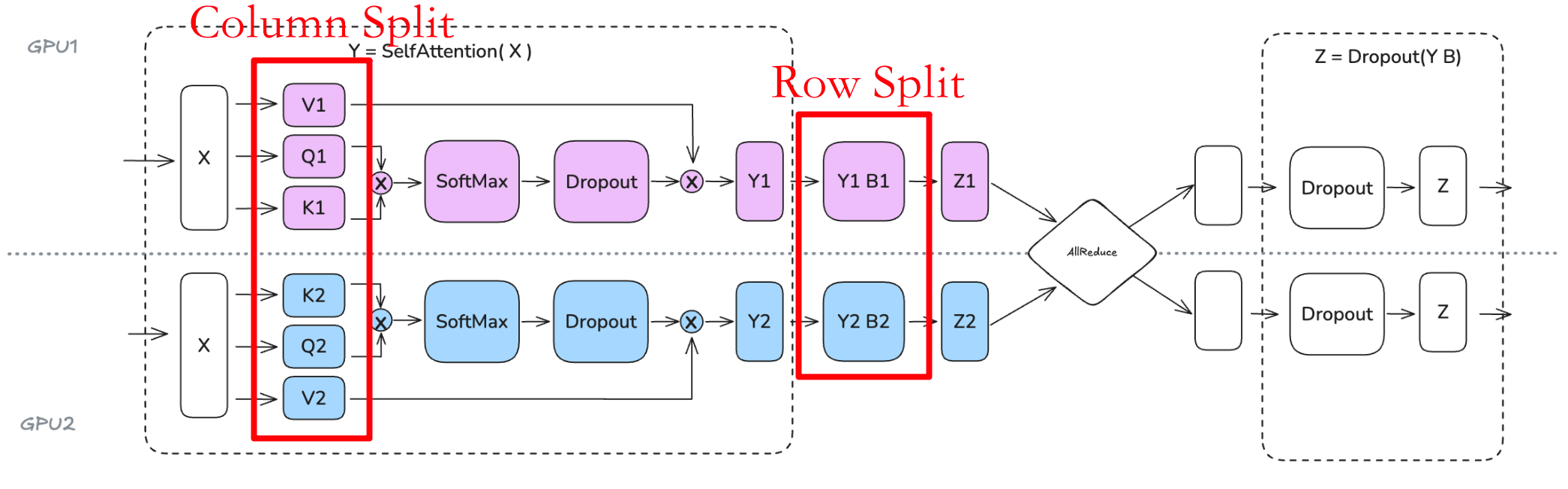
最后需要注意的是，Tensor Parallelsim 仍然不是训练的万能解决方案。我们在模型的计算路径中直接添加了几个分布式通信原语，因此这些原语难以完全隐藏/重叠于计算（就像我们在 ZeRO 中所做的那样），最终性能将是计算和内存增益与增加的通信开销之间的权衡结果。让举例说明：

观察 张量并行 MLP（同样适用于注意力机制）的操作时间线，我们可以更好地理解其中涉及的 trade-off。在每个解码器层的正向传播中，会遇到一个与 AllReduce 操作同步的点，这个点不能与计算重叠。这种通信开销是必要的，以便在最终应用 LayerNorm 之前，将张量并行等级的局部结果组合起来(PS: 否则结果便不正确了。

备注：

通过执行块矩阵乘法与异步通信/计算相结合，可以部分隐藏这种通信。例如，Megatron-LM/Nanotron 实现了 all-reduce 与 FC1 计算的局部重叠，其中矩阵乘法结果的一部分将开始发送到其他 GPU，而另一部分仍在计算中。

张量并行 TP 确实有助于减少矩阵乘法中的激活内存，因为中间激活被分发到多个 GPU 上。然而，我们仍然需要收集全量激活以进行如 LayerNorm 等操作，这意味着我们没有获得本可以得到的全部内存优势。

此外，TP 引入了显著的通信需求，这严重依赖于网络基础设施。无法完全隐藏这种特定的 All-Reduce 操作在计算背后的能力意味着它直接增加了前向传播的关键路径。

下面讨论 TP degree 对并行的影响：

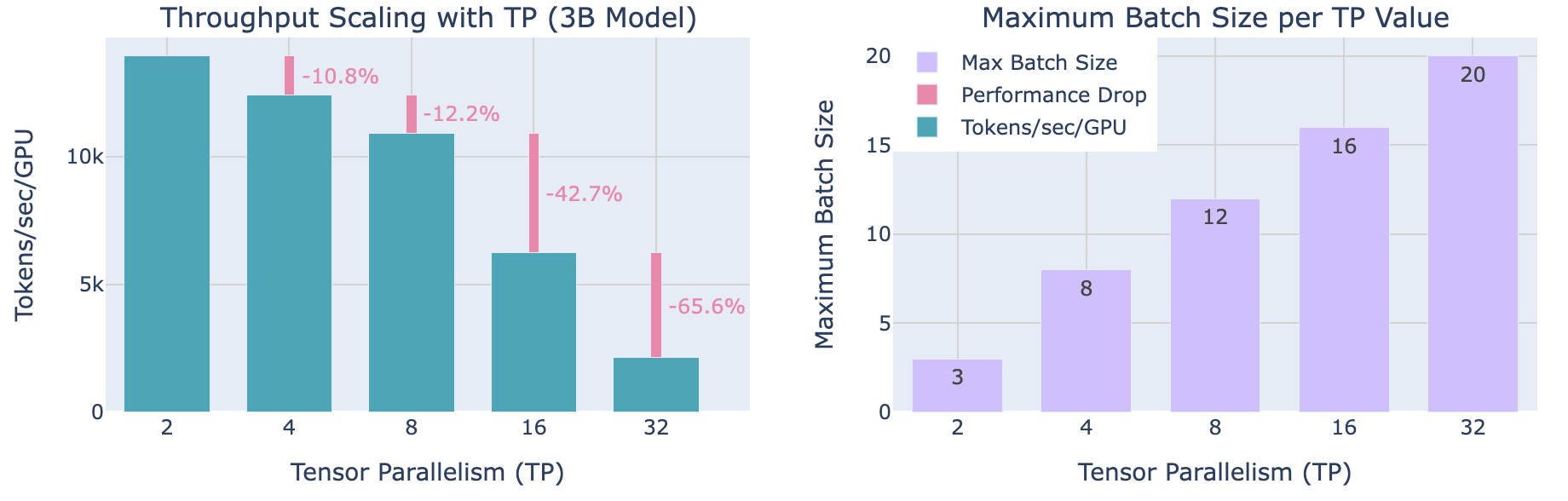
尽管随着 TP 的增加会导致每 GPU 吞吐量降低（左侧图所示），TP 使得处理更大的batch size成为可能（右侧图片所示），这说明了在分布式训练中计算效率与内存可用性之间的trade-off。

在实践中，正如我们在左图上所看到的，当扩展到超过 8 个 GPU 时，张量并行的通信开销变得尤为明显。虽然单个节点内的张量并行可以利用快速的 NVLink 互连，但跨节点则需要较慢的网络连接。我们从 TP=8 到 TP=16 时观察到显著的下降，从 TP=16 到 TP=32 时下降更为陡峭。在更高的并行度下，通信开销变得如此之高，以至于它迅速主导了计算时间。

总的来说，张量并行通过在多个 GPU 上分布模型参数、梯度、优化器状态和激活（在一定程度上）来为内存使用提供重要优势。让我们以一个 70 B的模型为例来考察这种效果：

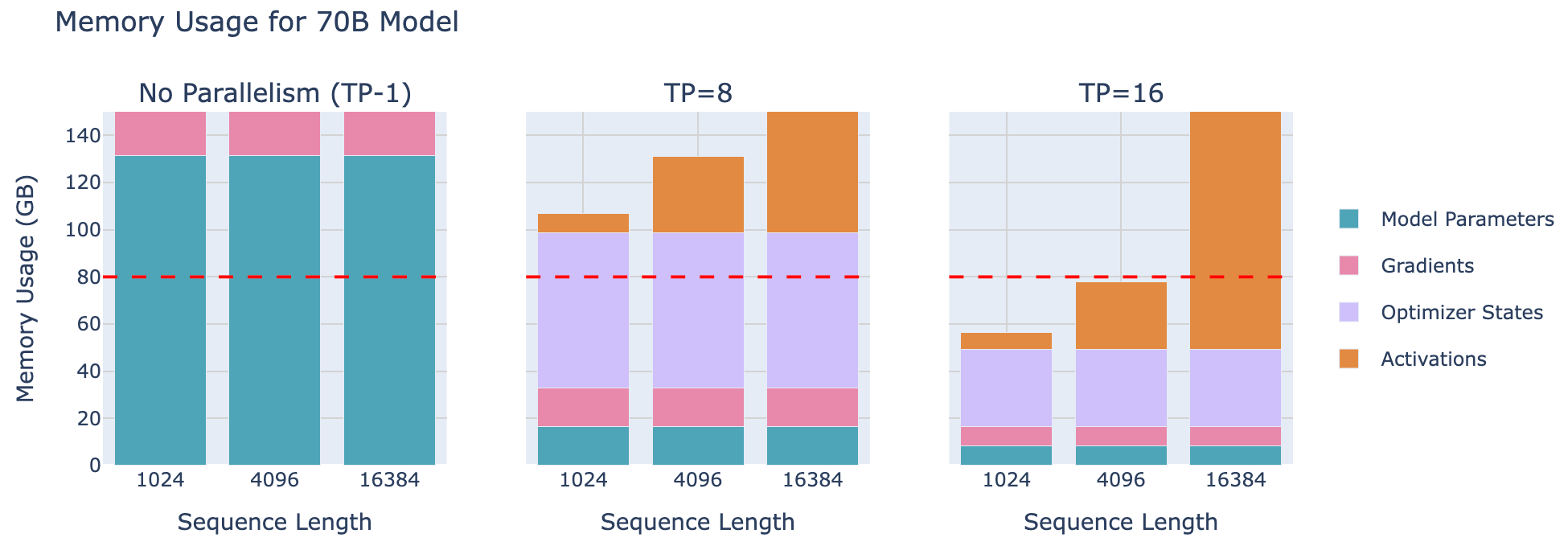
增加张量并行度可以降低每个 GPU 上模型参数、梯度和优化器状态所需的内存，直至可以开始在单个 8 GPU 节点上训练LLM。

是否存在一种方法能从这项技术中获得更多好处？我们已经看到，LayerNorm和 dropout 仍然需要在每个 GPU 上收集完整的激活，这在一定程度上抵消了内存节省的效果。我们可以通过找到并行化这些剩余操作的方法来做得更好。

关于张量并行训练中 Layer Normalization 一个点——由于每个 TP rank 在 all-gather 之后看到相同的激活，LayerNorm的权重实际上在反向传播后不需要 all-reduce 来同步它们的梯度。它们自然地在 Rank 间保持同步。然而，对于 dropout 操作，我们必须确保在 TP Rank间同步随机种子，以保持确定性。

编者注：在张量并行训练中，每个设备（rank）通过all-gather操作获取相同的激活值后，层归一化（layer normalization）的输入是相同的。因此，每个设备计算的层归一化权重（gamma和beta）的梯度是相同的，不需要额外的 all-reduce 操作来同步梯度，因为它们已经自然一致。这是因为所有设备基于相同的输入和梯度计算，梯度本身就是同步的。

参考文献

[1] https://huggingface.co/spaces/HuggingFaceFW/blogpost-fineweb-v1

[2] https://github.com/huggingface/picotron

[3] https://github.com/huggingface/nanotron

[4] https://filecdn.minimax.chat/_Arxiv_MiniMax_01_Report.pdf

[5] https://zdevito.github.io/2022/08/04/cuda-caching-allocator.html

[6] https://michaelwornow.net/2024/01/18/counting-params-in-transformer

[7] https://github.com/microsoft/DeepSpeed/issues/1773

[8] https://www.determined.ai/blog/act-mem-2

[9] Reducing Activation Recomputation in Large Transformer Models

Sequence Parallel 序列并行

序列并行性（SP）涉及将模型中由张量并行性（TP）未处理的部分（如 Dropout 和 LayerNorm）, 对于activation (shape为 [ bs, seq len, hidden dimension]沿输入序列维度( seq len) 进行拆分，而不是hidden dimension.

序列并行性这个术语有点过载：本节中的序列并行性 SP 与张量并行性 TP 紧密耦合，并适用于 dropout 和 层归一化 操作。然而，当我们转向更长的序列时，注意力计算将成为瓶颈，这需要像 Ring-Attention这样的技术，这些技术有时也被称为 序列并行性 SP，但我们将它们称为 上下文并行 Context Parallel 以区分两种方法。所以每次你看到序列并行性时，请记住它是与张量并行性一起使用的（与可以独立使用的上下文并行性相对）。

之所以在LayerNorm之前需要 all-reduce 是因为其需要完整的hidden dimension 来计算均值和方差。

$$
LayerNorm(x) = γ · \frac{x - μ}{\sqrt{σ^2 + ϵ}} + β
$$

其中 μ = mean(x), σ² = var(x) 需要在 hidden dimension h 上计算。

尽管这些操作在计算上非常cheap，但它们仍然需要大量的activation memory，因为它们需要完整的隐藏维度。SP 允许我们通过沿 序列维度seq 分割来将这个内存负担分发到多个 GPU 上。

在实践中，我们将从左图过渡到右图：

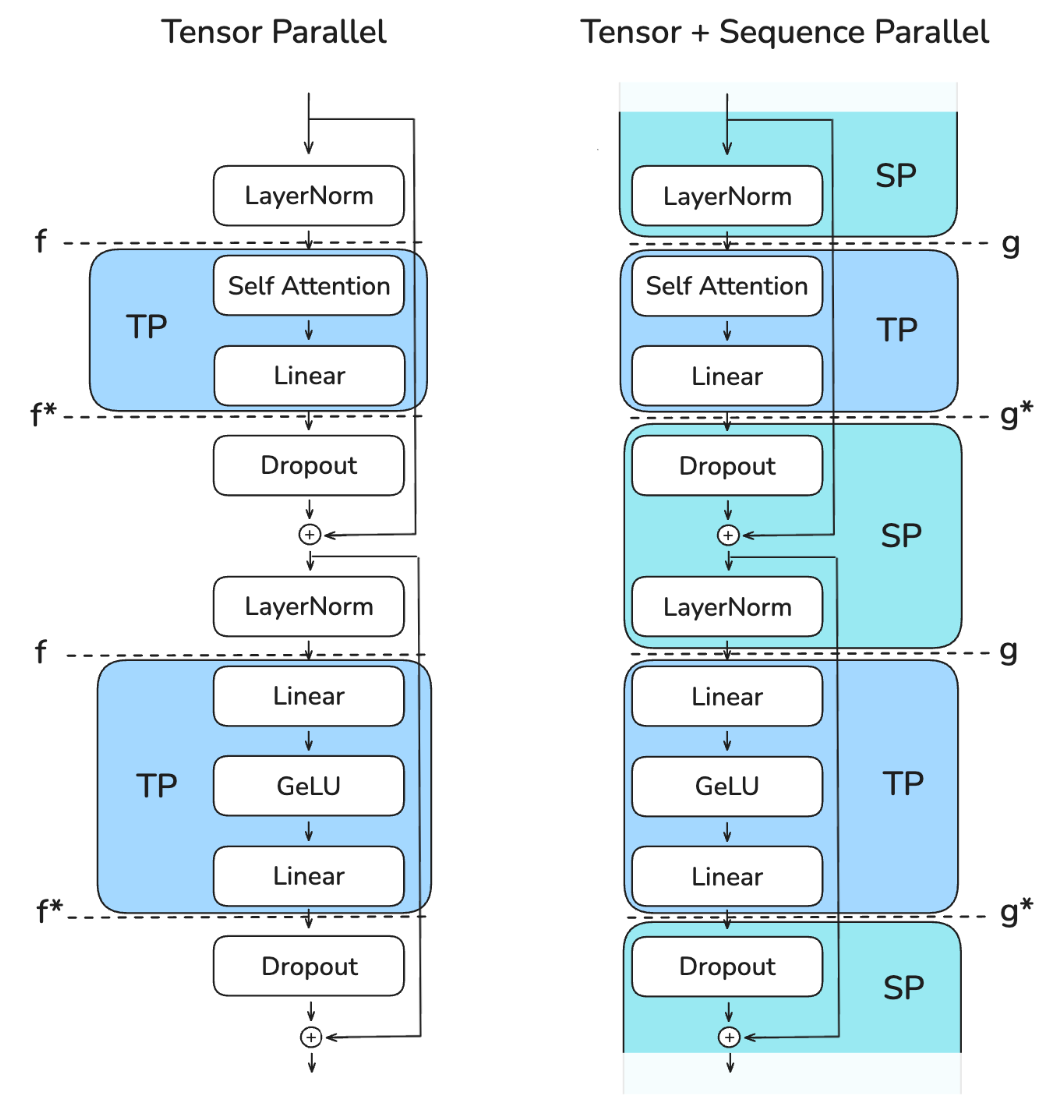
该图展示了如何通过不同的 Collective Operations（标记为“f”和“g”）在张量并行和序列并行区域之间进行转换。关键挑战是在保持内存使用低的同时确保正确性，并高效地管理这些转换。

在前向传播中：

  • “f” 是一个空操作（no operation），因为激活已经在各个 rank 之间复制。
  • “f*” 是一个 all-reduce 操作，用于同步激活并确保正确性

在反向传播中：

  • “f*” 是一个空操作，因为梯度已经在各个 rank 之间重复了
  • “f” 是一个 all-reduce 操作，用于同步梯度

这些操作 “f” 和 “f*” 被称为共轭对，因为它们相互补充——当一个在正向操作中为无操作时，另一个在反向操作中为全归约，反之亦然。

对于序列并行性（SP），我们使用标记为“g”和“g*”的不同操作。具体来说，我们避免在 SP 区域使用 all-reduce，因为这需要收集全部激活值并增加我们的峰值内存使用，从而违背了 SP 的目的。下面详细展开：

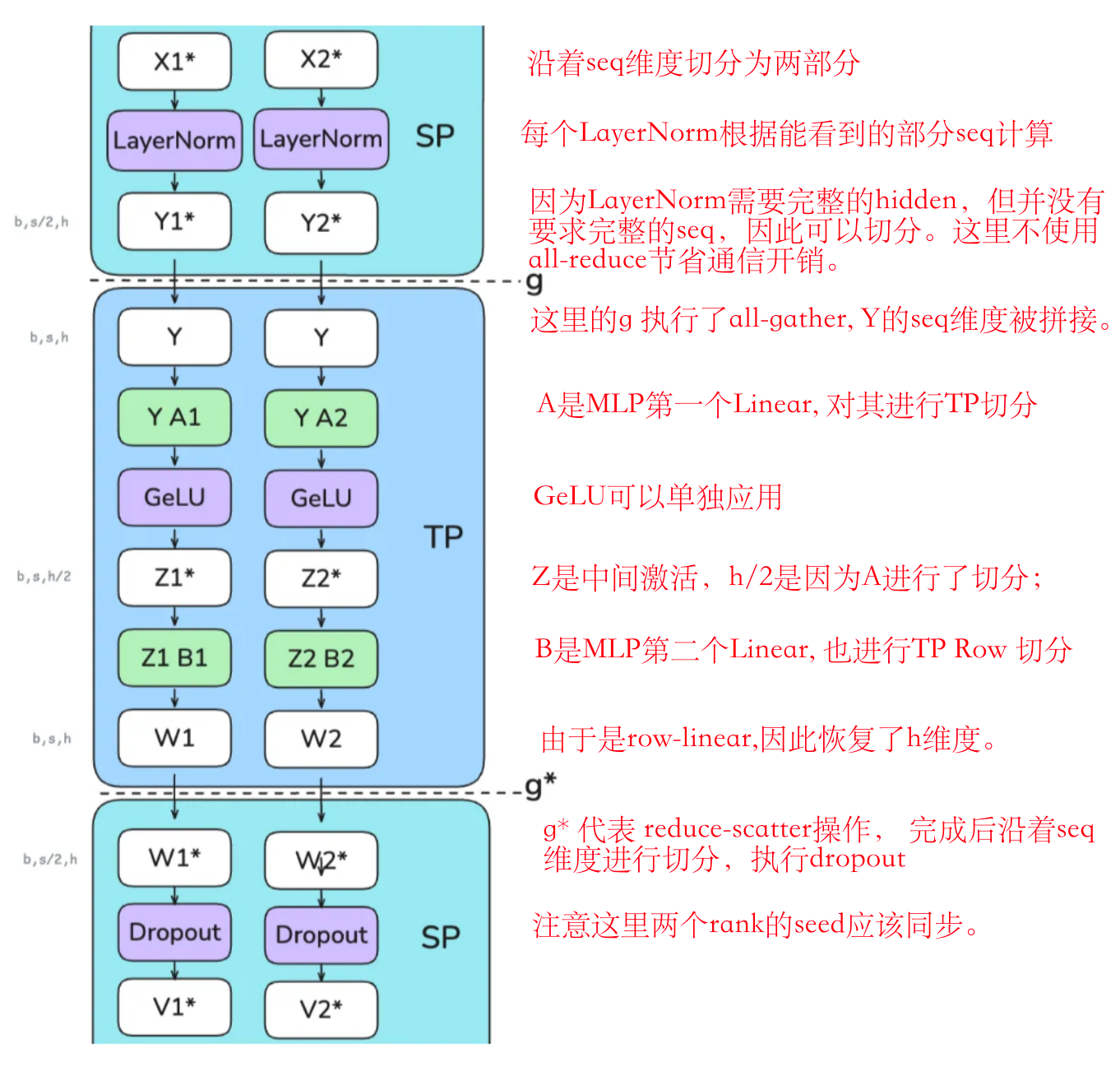
序列并行的一个关键优势是，它减少了我们需要存储的最大激活大小。在仅使用张量并行时，我们必须在多个点存储形状为（b,s,h）的激活值。然而，通过使用序列并行，最大激活大小减少为 b⋅s⋅h / tp ，因为我们总是沿着序列维度或隐藏维度进行分割。

用表格来总结以上分片过程(part1: hidden size和seq维度变化；

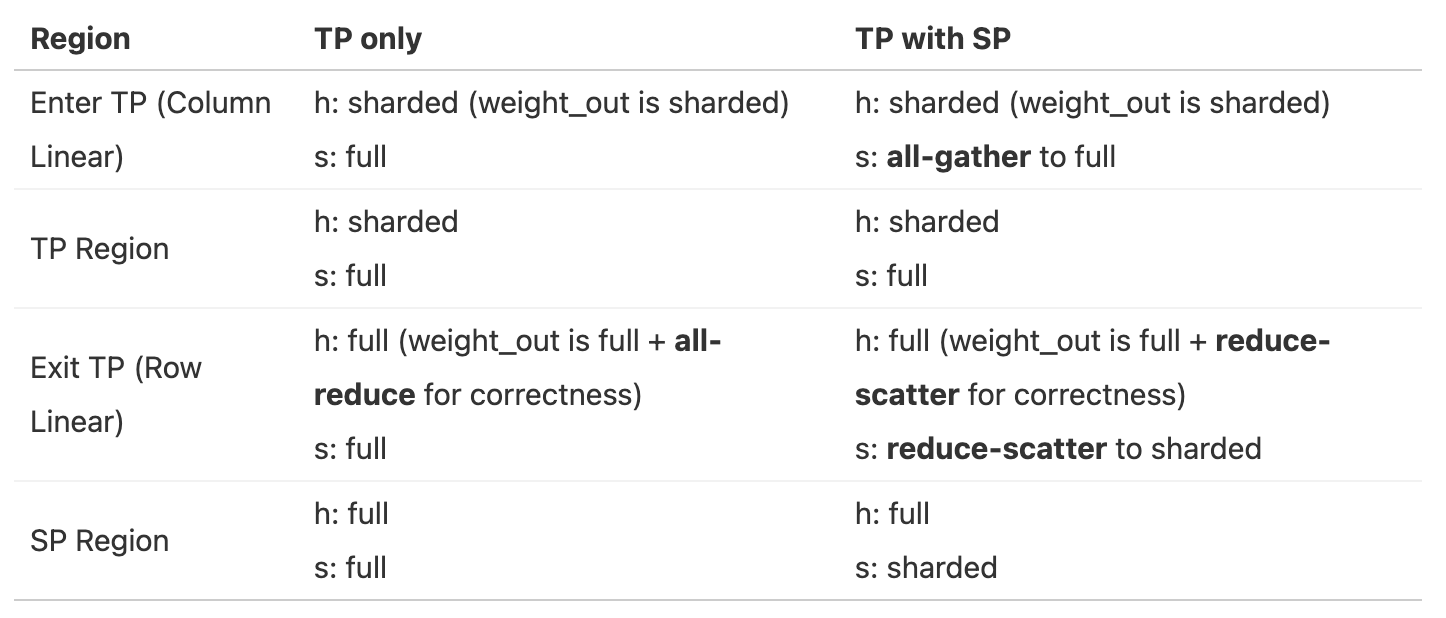
（part2: embedding Layer变化；

再看一下使用了SP以后的激活情况，跟上图对比，SP可以大幅度降低每个GPU的mem占用，尤其是对16k长序列场景下。

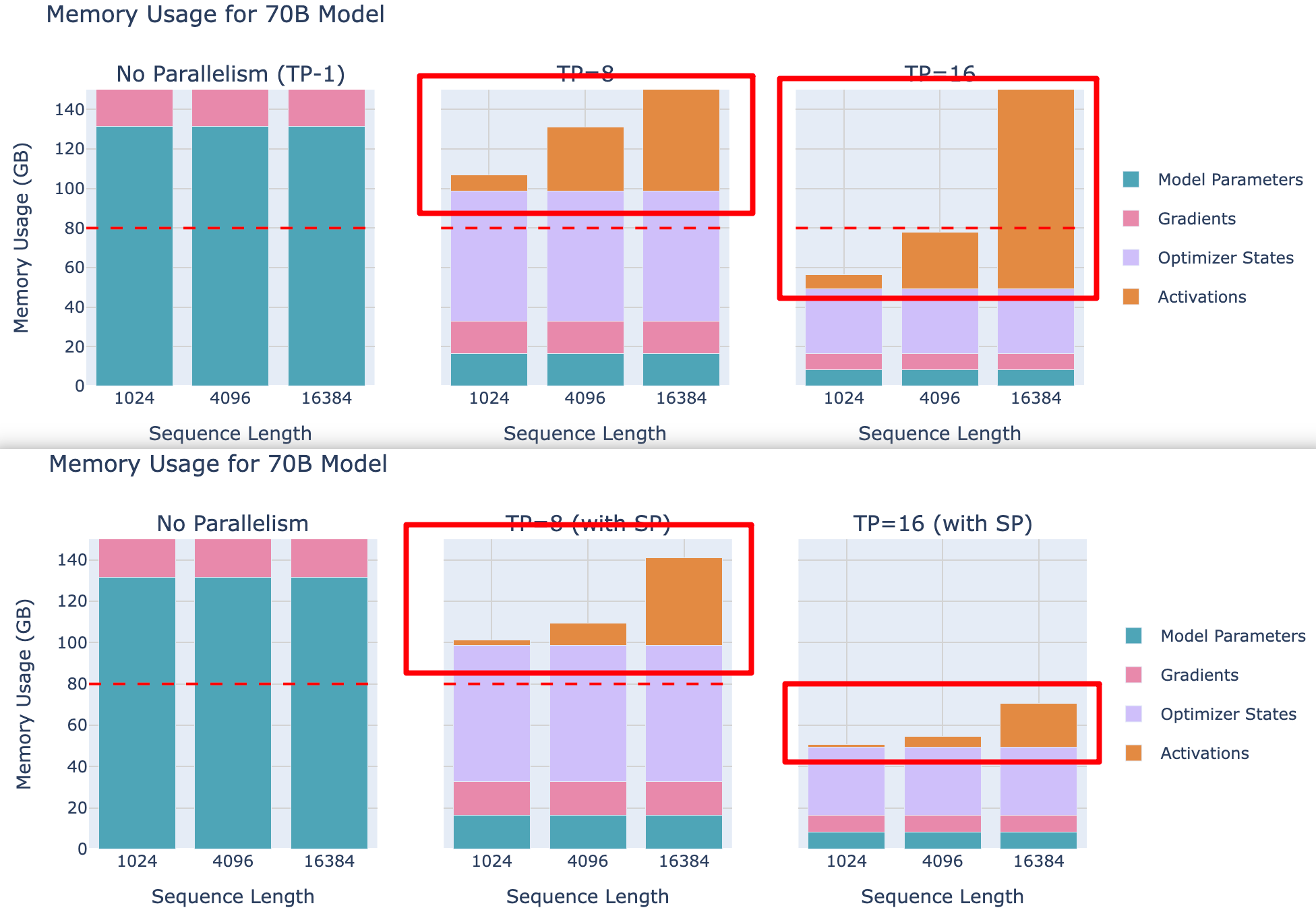
TP+SP是否会比单纯TP更耗通信？

  • 在纯 TP 的前向传播中，我们每个 Transformer 块有两个 all-reduce 操作，而在 SP 中，我们每个 Transformer 块有两个 all-gather 和两个 reduce-scatter 操作。所以 SP 的通信操作数量是 TP 的两倍。
  • 但是由于 all-reduce 操作可以被分解为 all-gather + reduce-scatter，它们在通信方面实际上是等效的。对于反向传播，只是使用每个操作的共轭（no-op = all-reduce 和 all-gather = reduce-scatter），推理方式相同。

编者注：All-reduce 可以分解为 reduce-scatter 和 all-gather，因为 reduce-scatter 先归约并分发数据，all-gather 再收集完整结果。

使用TP+SP的 profiling如下图所示，每层有4个通信操作（2个来自MLP，两个来自MHA)：

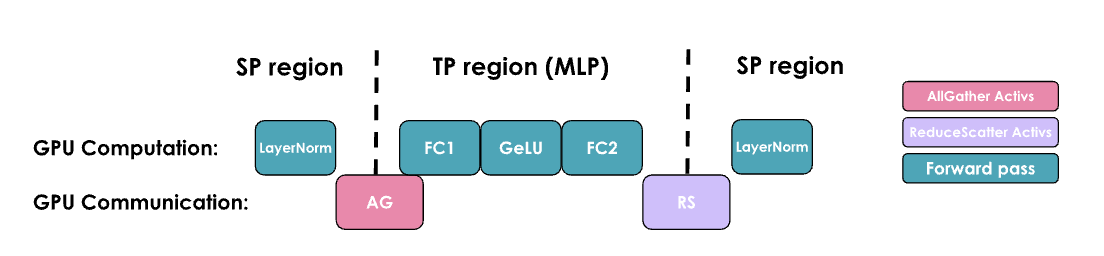
就像传统的TP一样，TP+SP也不能轻易与计算操作重叠，这使得吞吐量在很大程度上依赖于通信带宽。这里，像传统TP一样，TP+SP通常只在单个节点内进行（保持TP度数不超过每个节点的GPU数量，例如TP≤8）。

下面继续benchmark，随着TP rank增加，通信开销变化（实验setting seq len 4096, 模型大小3B)：

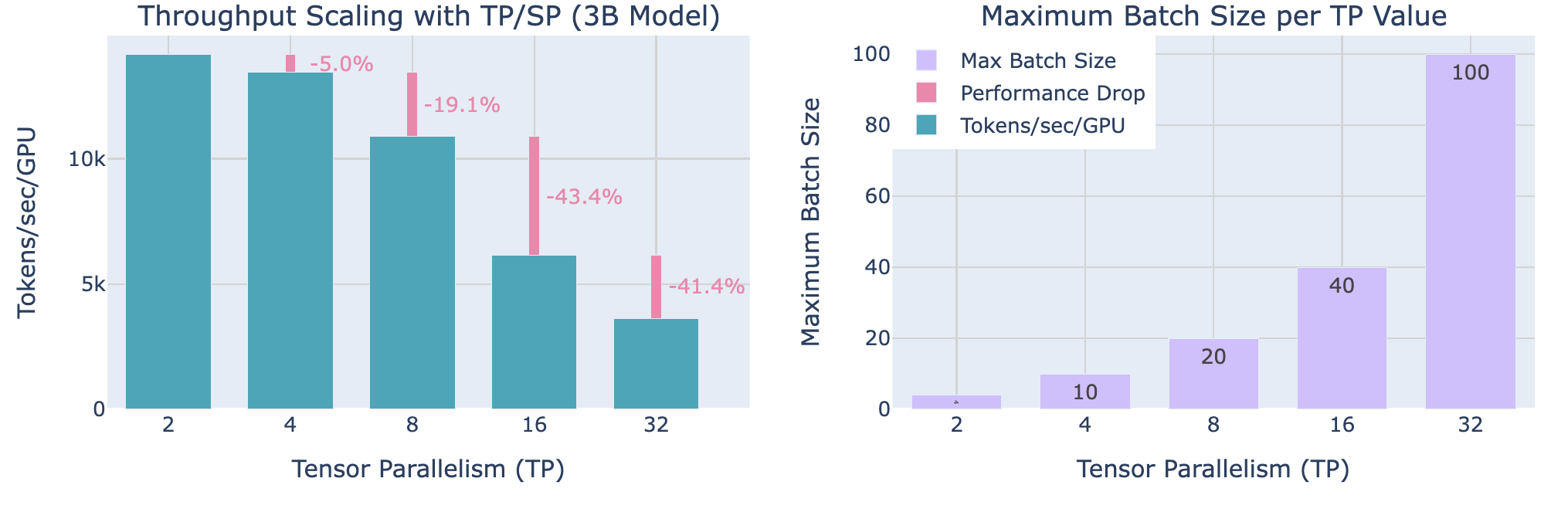
可以得出结论：虽然更高的并行度通过减少激活内存使得处理更大的Batch成为可能，但它们也会减少每个GPU的吞吐量，特别是当并行度超过节点内GPU数量时。

总结一下观察结果：

  • 对于这两种方法，注意到从TP=8移动到TP=16时，性能下降最为明显，因为这是从仅在单个节点内（NVLink）通信，转向跨节点通信（EFA）的时候。
  • 使用TP和SP时，激活的内存节省帮助我们适应比仅使用TP时更大的Batch。

到这里我们已经看到 TP 如何通过沿隐藏维度分割注意力和前馈操作，将激活操作分割到多个 GPU 上，以及 SP 如何通过沿序列维度分割，自然地补充了TP。

注意：

由于SP区域中的LayerNorm操作在序列的不同部分进行，因此它们的梯度将在TP的不同rank之间有所不同。为了确保权重保持同步，我们需要在反向传播过程中对它们的梯度进行all-reduce操作，这类似于数据并行（DP）中确保权重同步的方式。然而，由于LayerNorm的参数相对较少，这个通信开销较小。

然而，TP和SP有两个限制：1️⃣ 如果增加序列长度，激活内存在TP仍然会膨胀；2️⃣ 如果模型太大，无法适应TP=8，那么由于跨节点连接性问题，遇到巨大的性能下降。

可以通过Context Parallel上下文并行解决问题 1️⃣ ；用Pipeline Parallel流水线并行解决问题 2️⃣；

Context Parallel 上下文并行

通过张量并行TP和序列并行SP，可以显著降低每个GPU的内存需求，因为模型权重和激活值均分布在各个GPU上。然而，当训练的序列越来越长（例如当每个序列扩展到128k个token甚至更多时），仍可能超出单节点可用内存，因为在TP区域内仍需处理完整的序列长度。

此外，即使采用gradient checkpointing 的方法（这会带来约30%的沉重计算开销），我们仍需在内存中保留部分层边界的激活值，而这些激活值随序列长度呈线性增长。来看看上下文并行如何帮助我们：

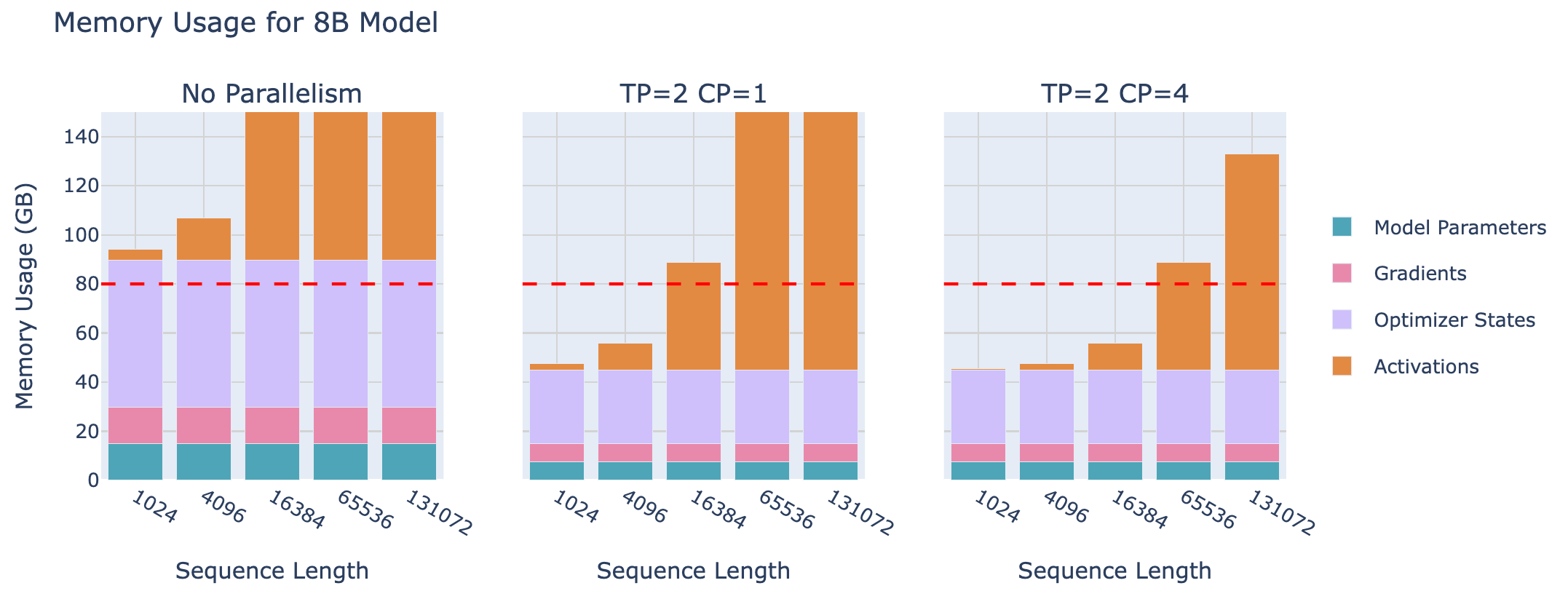
上下文并行的核心思想是**将序列并行的方法（也就是沿序列长度进行拆分）**的思路应用到已经采用张量并行的模块上。我们将对这些模块沿两个维度进行拆分，从而也减少序列长度带来的影响。经过前面所讨论的内容，你会发现这种方法非常直观，但这里有一个技巧，所以请保持警惕！

对于上下文并行CP，就像序列并行SP一样，将沿序列维度拆分输入，但这次我们对整个模型进行拆分，而不仅仅是对之前Tensor+Sequence并行中涉及的部分模型。

  • 拆分序列不会影响大多数模块，如MLP和LayerNorm，因为它们对每个token的处理是独立的。它也不像TP那样需要昂贵的通信，因为只拆分了输入而非权重矩阵。就像数据并行一样，在计算梯度后，会启动一次all-reduce操作以在上下文并行组内同步梯度。
  • 有一个重要例外需要特别注意，那就是注意力模块。
    • 在注意力模块中，每个token需要访问来自所有其他序列token的键/值对；
    • 在Casual Attention 的情况下，至少需要关注每个前面的token。
  • 由于上下文并行是沿序列维度将输入分布到各个GPU上，注意力模块将需要各个GPU之间进行充分通信，以交换必要的键/值数据。

如果采用简单的方法会非常昂贵。但有没有办法能更高效、更快速地完成这一操作呢？幸运的是，有一种核心技术可以高效地处理键/值对的通信，叫做环形注意力 Ring Attention。

注意：

上下文并行性与 Flash Attention 在概念上存在一些相似之处——这两种技术都依赖于在线 softmax 计算以减少内存使用。虽然 Flash Attention 专注于在单个 GPU 上优化注意力计算本身，而上下文并行性通过将序列分布到多个 GPU 上实现内存减少。

发现环状注意力 Ring Attention

在这个注意力机制的实现中，每个 GPU 首先启动异步通信操作，将其键/值对发送到其他 GPU。在等待其他 GPU 的数据时，它计算内存中已有数据的注意力分数。理想情况下，在完成计算之前，从另一个 GPU 接收到下一个键/值对，使 GPU 能够在完成第一次计算后立即开始下一轮计算。

举例说明。假设有 4 个 GPU 和一个包含 4 个Token的输入。最初，输入序列在序列维度上均匀分割，因此每个 GPU 将恰好有一个Token及其对应的 Q/K/V 值。假设 Q1、K1 和 V1 分别代表第一个Token的查询、键和值，它们位于第 1 个 GPU 上。注意力计算需要 4 个时间步来完成。在每一个时间步，每个 GPU 执行这三个连续操作：

  1. 以非阻塞的方式将“当前的K和V”发送给下一台机器（在非阻塞模式下的最后一个时间步除外），以便在此步骤尚未完成时即可开始下一步骤
  2. 在本地对已拥有的“当前K和V”计算注意力得分 Attention Score.
  3. 等待接收来自上一台GPU的K和V，然后返回到步骤1，此时“当前的K和V”即为刚刚从上一台GPU接收到的K/V对。

执行这 3 个步骤四次以完成注意力计算。

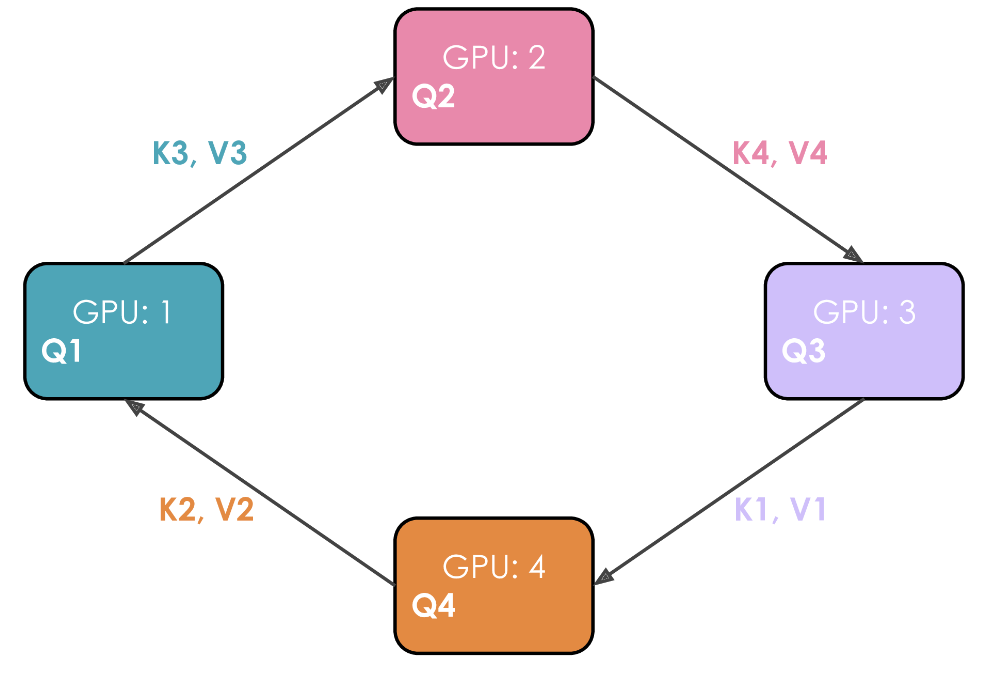
从上图中很明显就能看出作者为什么选择将这种方法称为环状注意力。

然而有一个大问题，那就是环状注意力（Ring Attention）的简单实现导致因果注意力矩阵的形状产生了强烈的失衡。让通过考虑带有因果注意力掩码的注意力得分矩阵来查看 SoftMax 的计算：

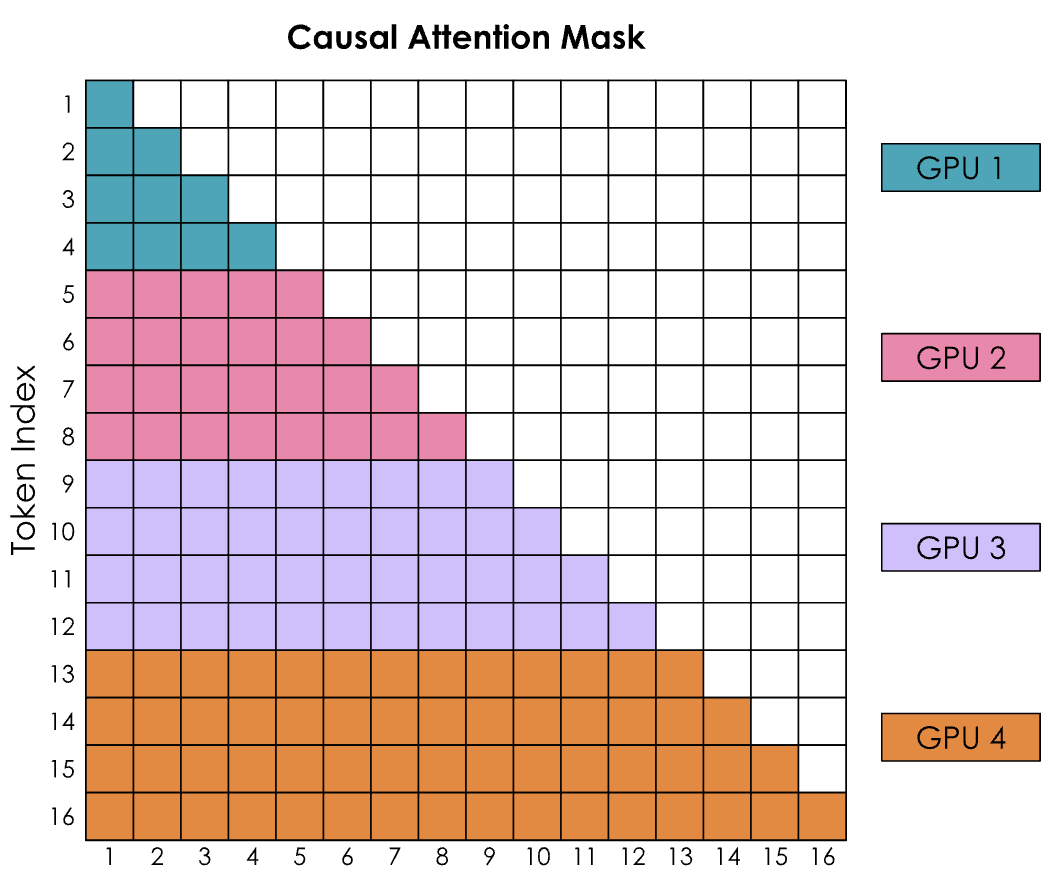
编者注：在Transformer模型的注意力机制中，这种矩阵通常表示注意力掩码，其中行（y轴）代表查询（query）token，列（x轴）代表键（key）token。矩阵中的每个单元格（y, x）表明查询token y是否可以关注键token x。

SoftMax 是按行计算的，这意味着每当 GPU 收到一行中的所有标记时，就可以进行计算。

  • GPU1 可以立即计算，因为它从标记 1-4 开始，而 GPU1 实际上不需要从任何其他 GPU 接收任何信息。
  • GPU2 将需要等待第二轮才能也收到 1-4，从而获得标记 1-8 的所有值。此外，GPU1 似乎比所有其他 GPU 的工作量都要少。

如何更好的平衡计算呢？

Zig-zag Ring Attention 平衡版本实现

我们需要一种更好的方法来分配输入序列。这可以通过将非纯顺序的标记分配给 GPU，并通过稍微混合排序，使得每个 GPU 上都有早期和晚期标记的良好混合来实现。这种方法被称为之字形注意力 Zig-zag Ring Attention。

在这个新的配置中，注意力掩码将显示计算分布均匀，但如果计算彩色方格的数量，会发现计算现在均衡分布在所有 GPU 上。

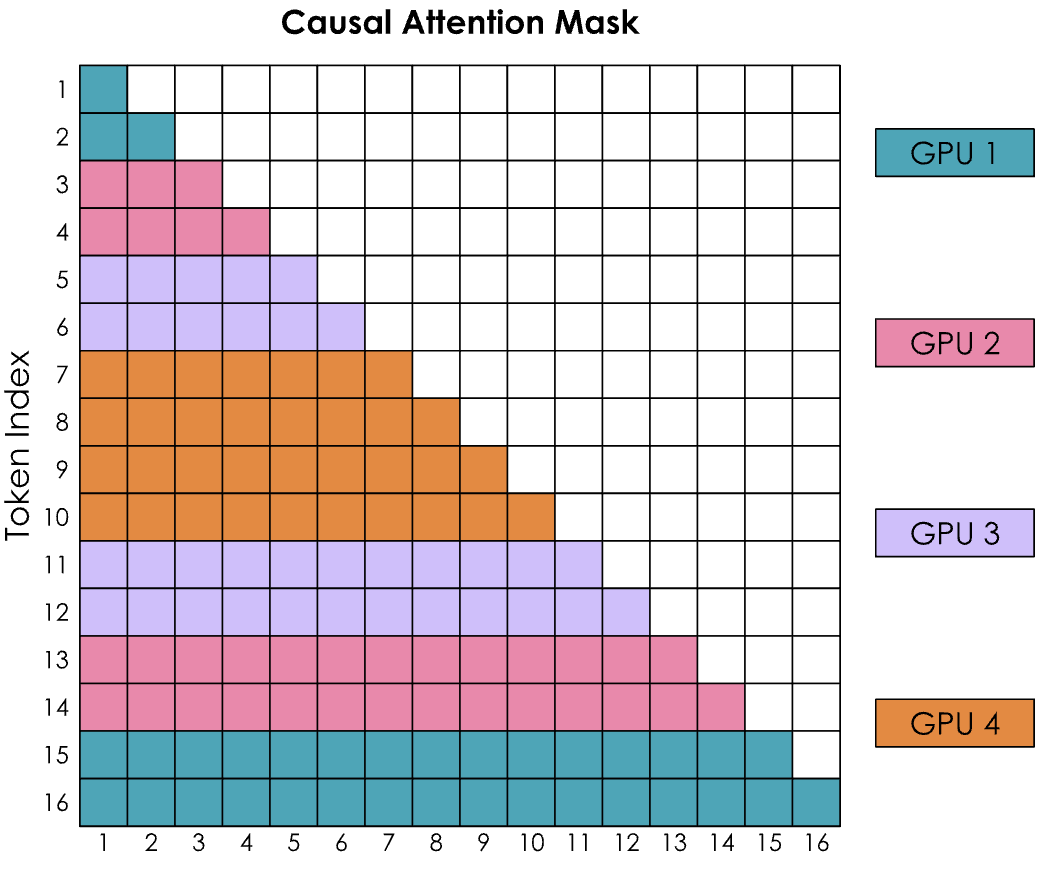
同时也会看到，为了完成所有行，每个 GPU 都需要从所有其他 GPU 获取信息。

一般有两种常见方式来重叠计算和通信：一种是通过执行一次通用的 all-gather操作，同时在每个GPU上重新组合所有KV（类似于Zero-3的方式）；另一种是根据需要从每个GPU逐个收集KV对：

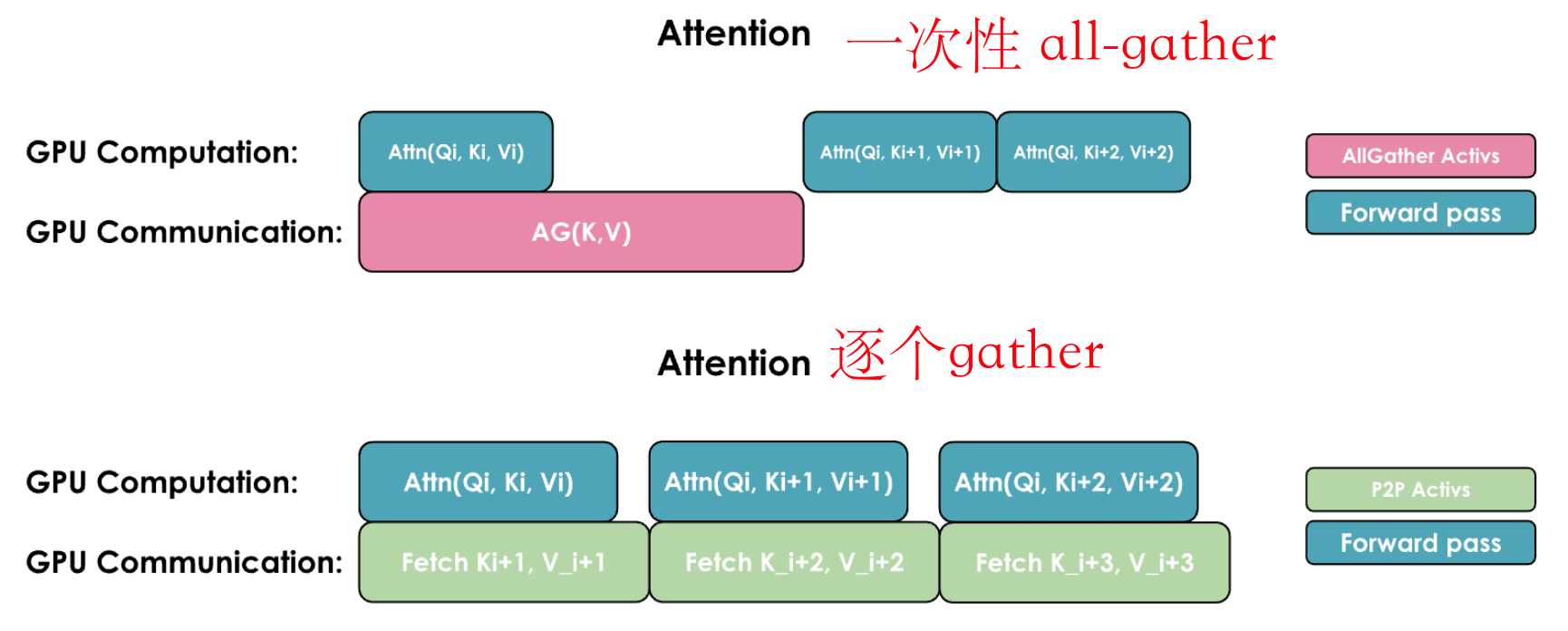
这两种实现方式的关键区别在于它们的通信模式和内存使用：

1. All-Gather实现：

  • 所有GPU同时收集来自其他所有GPU的完整键/值对
  • 需要更多的临时内存，因为每个GPU需要一次性存储完整的KV对
  • 通信在一步内完成，但伴随较大的内存开销

2. All-to-All（Ring）实现：

  • GPU以环形模式交换KV对，每次传输一个数据块
  • 更节省内存，因为每个GPU只需临时存储一个数据块
  • 通信被分发并与计算重叠，尽管由于多次通信步骤会带来一些额外的基础延迟

到目前为止，我们已经看到如何通过TP在单个节点上拆分模型以驯服大模型，以及如何利用CP应对长序列带来的激活值爆炸问题。

然而，TP在跨节点扩展时并不理想，那么如果模型权重难以容纳在单个节点上，该怎么办？这时，另一种并行度——流水线并行，将派上用场！

Pipeline Parallel 流水线并行

在TP部分，当张量并行度超过单个节点的GPU数量（通常为4或8）时，会遇到带宽较低的“跨节点连接”，这会严重影响性能。可以通过在集群的多个节点上基准测试 all-reduce 操作清楚地看到这一点（每个节点有8块GPU）：

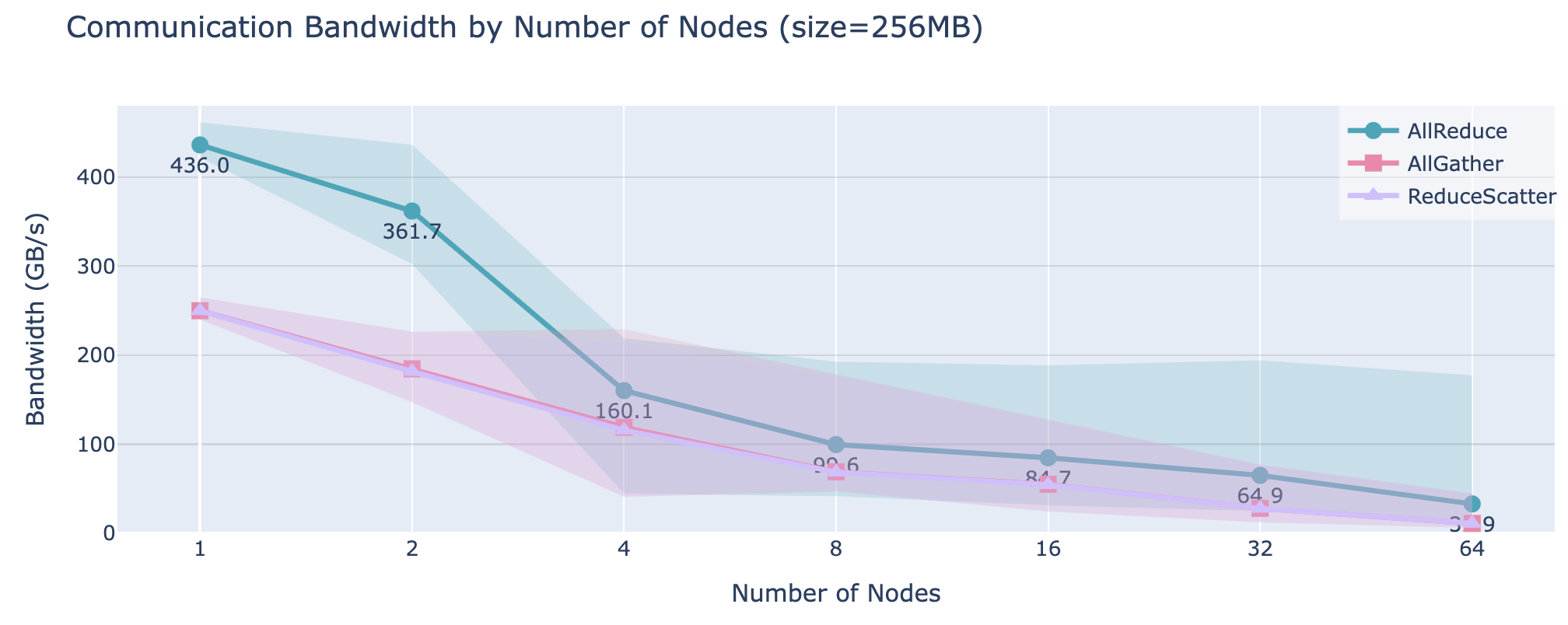
序列并行SP和上下文并行CP对于长序列有帮助，但如果序列长度并不是导致内存问题的根本原因，而是模型本身的大小，那么它们的作用就相对有限。

对于大模型（70B+），仅权重的大小就可能超出单个节点的4-8块GPU的承载能力。可以通过引入第四种（也是最后一种）并行方式来解决这个问题：“流水线并行 Pipeline Parallel”。

流水线并行是一种简单但强大的技术——将模型的层划分到多个GPU上！例如，如果有8块GPU，可以将第1-4层放在GPU 1上，第5-8层放在GPU 2上，以此类推。这样，每块GPU只需要存储和处理部分模型层，大幅减少了每块GPU的内存需求。来看看流水线并行在8B模型上的内存使用效果：

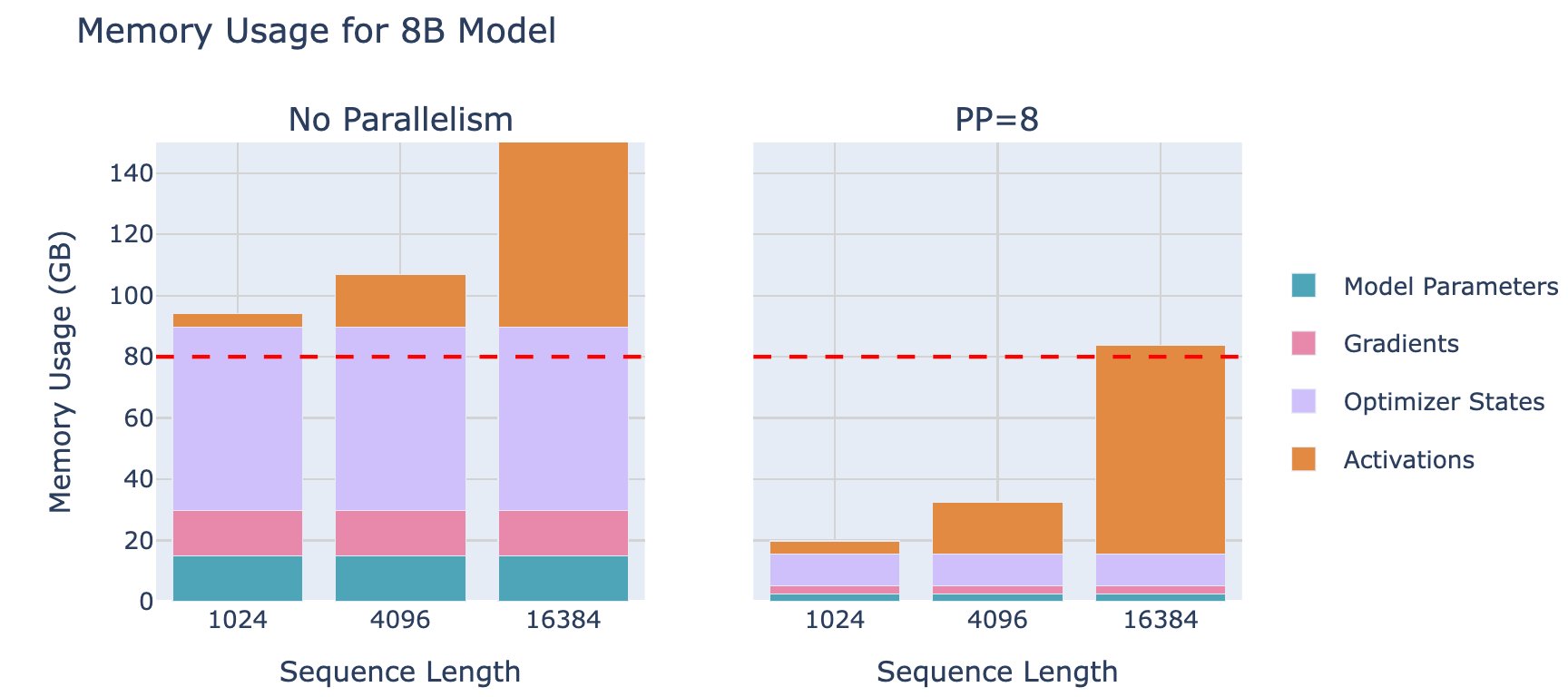
可以发现：虽然模型参数被很好地拆分到多个GPU上，但每块GPU上的激活内存仍然保持不变！这是因为每块GPU仍然需要处理整个数据Batch，只是处理的层不同。一个GPU计算出的激活将被发送到下一个GPU，以继续完成前向传播。

编者注：PP让人想到Zero-3的模型拆分，但是他们存在区别：
(1) PP 将模型按照层（layer）纵向分割成多个阶段（stage），每个阶段分配给不同的计算设备（通常是 GPU）。比如，一个有 32 层的模型可以被分成 4 个阶段，每阶段包含 8 层，由 4 个 GPU 分别处理。(2)Zero3 并不直接按层分割模型，而是将模型的参数（权重、梯度和优化器状态）分片（shard）到多个设备上。每个设备持有整个模型的一部分参数，而不是特定的层。

这引入了一种新的通信模式：与ZeRO-3在数据并行中同步参数不同，在这里，我们是在GPU之间按顺序传递激活张量，形成一个“流水线”。虽然这个概念很简单，但高效地实现这一技术却颇具挑战。让我们深入探讨其具体细节！

在不同节点上拆分层 —— AFAB

假设简单地将模型的层分布到多个设备上，例如，第一个GPU处理前几层，第二个GPU处理模型的后续部分，以此类推。这样，前向传播过程就变成了依次将数据Batch沿着模型传递，并依次使用每个计算设备。

这种方法带来的第一个直接优势是：所需的互连带宽较低，因为只在模型的少数位置传输中等大小的激活值。与张量并行不同，张量并行需要在每层内部进行多次通信，而这里的通信次数要少得多。

你可能已经开始隐约察觉到即将出现的问题：“依次” 和 “顺序执行”？在并行计算的世界里，这听起来似乎效率不高，特别是在刚刚讨论了计算与通信重叠的重要性之后。

确实如此！流水线并行 PP 的主要挑战在于 如何有效地绕过这种顺序执行的限制，确保GPU始终保持忙碌，避免一个GPU在计算时，其他GPU处于等待状态。下面是一个简单的前向和反向传播示例，展示了GPU的利用情况（数字表示模型的层编号）, 展示了一个16层4卡流水线并行：

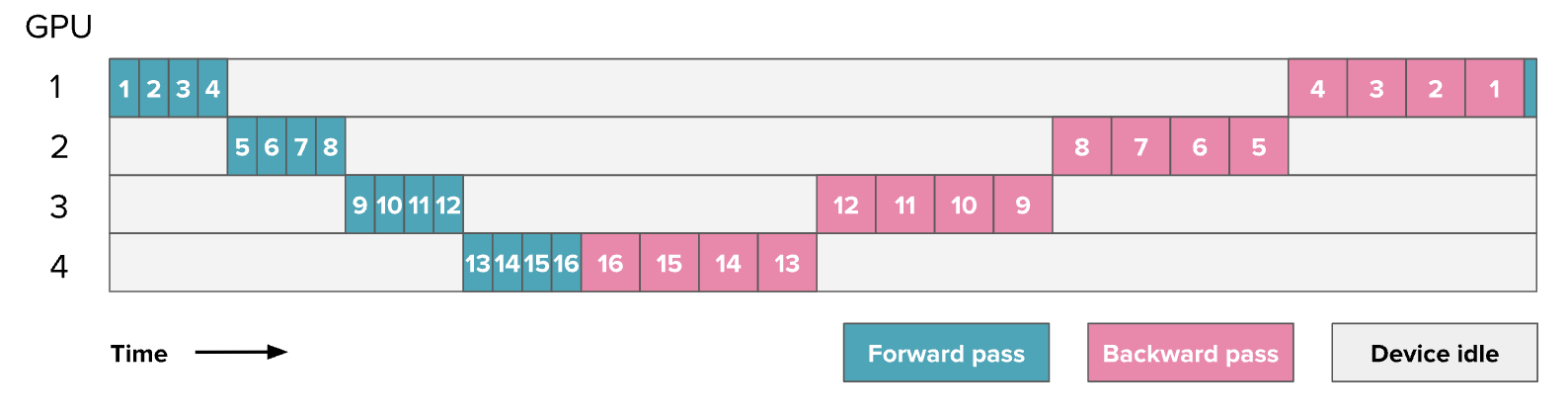
图中灰色部分表示剩余的空闲时间，通常称为“气泡（bubble）”。看到这些空闲时间，你可能会感到沮丧，毕竟我们已经花费了大量时间来优化吞吐量。我们可以通过计算“气泡”导致的额外时间来衡量流水线并行的效率。假设 $t_f$ 和 $t_b$分别是单个Micro Batch在流水线的一个阶段上进行前向传播和反向传播所需的时间（通常假设 $t_b≈2\times t_f$，在上图中可以观察到）。如果能够完美并行化，理想总时间应为 $t_{id}=t_f+t_b$。但由于流水线气泡的存在，额外的时间为 $t_{pb} = (p - 1) \times (t_f + t_b)$（其中 $p$ 是流水线并行度，即上图中的GPU数量），即每个GPU在其他GPU计算时的等待时间。可以计算额外气泡时间与理想时间的比值：

$$
r_{bubble} = \frac{(p - 1) \times (t_f + t_b)}{t_f + t_b} = p - 1
$$

当增加流水线数时，气泡时间随之增加，GPU利用率下降。可以看出，在一个简单的实现中，流水线气泡可能会非常大！幸运的是，已经有多种流水线并行方案被设计出来，以减少气泡的大小。

第一个优化方法是，将Batch拆分成更小的micro batches，使它们可以并行或近乎并行地处理，就像在数据并行中做的那样。例如，当第二块GPU在处理Micro-Batch1时，第一块GPU可以开始处理Micro-Batch2。以下是一个使用8个Micro-Batch的调度方案：

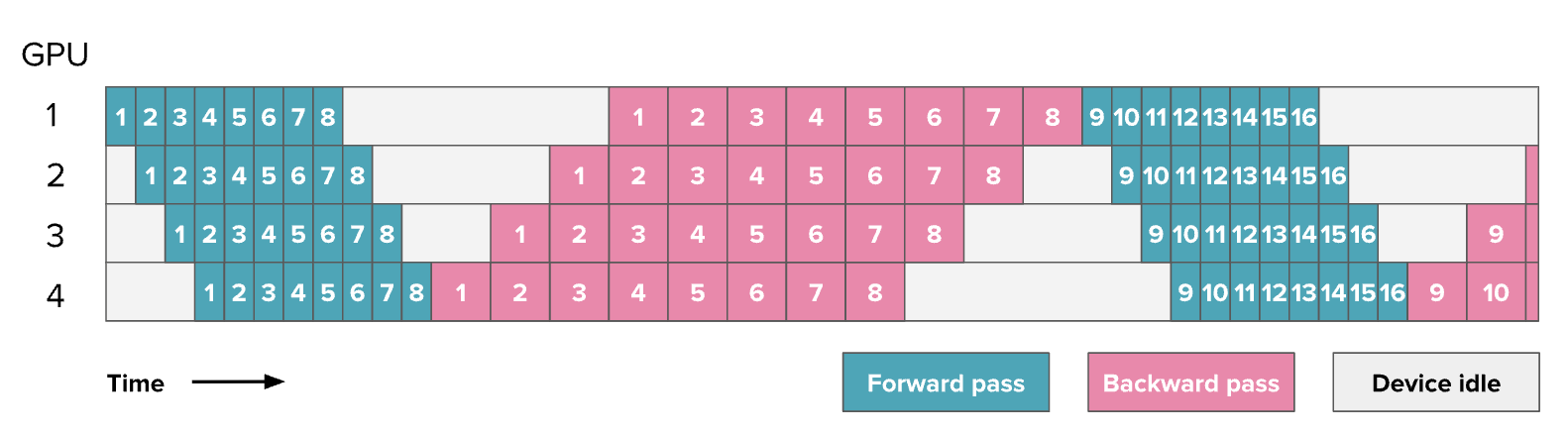
注意：

在之前的图表中，数字代表的是模型的层数，而从这一张图开始，所有流水线并行相关的图表中的数字都表示 Micro Batch。可以将每个方块理解为包含多个层，就像前一张图所示的那样。

上述调度方式被称为**全前向-全反向（AFAB, All-Forward-All-Backward）调度，因为它先执所有前向传播，然后再执行所有反向传播。

其优势在于前向和反向传播仍然是严格顺序的，因此可以保持模型训练代码的整体组织，使这种流水线并行实现方式成为最容易实现的一种。

下面是Picotron的AFAB 流水线实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
def train_step_pipeline_afab(model, data_loader, tensor_shapes, device, dtype):
    logging_loss: torch.float32 = 0.0
    input_tensors, output_tensors = [], []
    requires_grad_sync = pgm.process_group_manager.cp_dp_world_size > 1

  # 从这里开始分前向的micro batch
    for _ in range(data_loader.grad_acc_steps): # All forward passes
        input_tensor = pipeline_communicate(operation='recv_forward', shapes=tensor_shapes, device=device, dtype=dtype)
        batch = next(data_loader)
        batch["hidden_states"] = input_tensor.to(device) if input_tensor is not None else input_tensor
        output_tensor = model.forward(input_ids=batch["input_ids"].to(device), position_ids=batch["position_ids"].to(device), hidden_states=batch["hidden_states"])
        pipeline_communicate(operation='send_forward', tensor=output_tensor, device=device, dtype=dtype)
  
        # calculate loss on the last stage
        if pgm.process_group_manager.pp_is_last_stage:
            output_tensor = F.cross_entropy(output_tensor.transpose(1, 2), batch["target_ids"].to(device), reduction='mean')
            logging_loss += output_tensor.item() / data_loader.grad_acc_steps

        input_tensors.append(input_tensor)
        output_tensors.append(output_tensor)
  # 这里开始反向
    for ith_microbatch in range(data_loader.grad_acc_steps): # All backward passes
        if requires_grad_sync:
            is_last_iteration = (ith_microbatch == data_loader.grad_acc_steps - 1)
            model.require_backward_grad_sync = is_last_iteration
        output_tensor_grad = pipeline_communicate(operation='recv_backward', shapes=tensor_shapes, device=device, dtype=dtype)
        input_tensor, output_tensor = input_tensors.pop(0), output_tensors.pop(0)
        input_tensor_grad = model.backward(input_tensor, output_tensor, output_tensor_grad)
        pipeline_communicate(operation='send_backward', tensor=input_tensor_grad, device=device, dtype=dtype)

    return logging_loss

现在我们来估算这种方法的流水线气泡时间。在第一个示例中，理想情况下处理 $m$ 个Micro-Batch所需的时间为 $t_{id} = m \times (t_f + t_b)$：

$$
r_{bubble} = \frac{(p - 1) \times (t_f + t_b)}{m \times (t_f + t_b)} = \frac{p - 1}{m}
$$

可以通过增加Micro-Batch数量 $m$ 来减少流水线阶段的不效率，从而按 $m$ 的比例减少气泡的大小。

然而，除了气泡问题，还有另一个令人头疼的问题：存储所有激活值所需的内存。需要将所有的激活值保留在内存中，直到反向传播阶段开始，这会导致内存使用量迅速膨胀，从而使这些流水线并行实现变得不可行。那么，能否找到一种方法，避免这种内存膨胀呢？

既然内存膨胀是由反向传播阶段所需的激活存储导致的，可以尝试在仍然执行部分前向传播时就开始执行反向传播，这样可以尽早释放部分激活，减少内存占用。

这种方案被称为 One-forward-one-backward （1F1B), 因为中间/稳定状态涉及交替执行一次正向和一次反向传递。总体思路是尽可能早地开始执行反向传递。这个调度看起来是这样的：

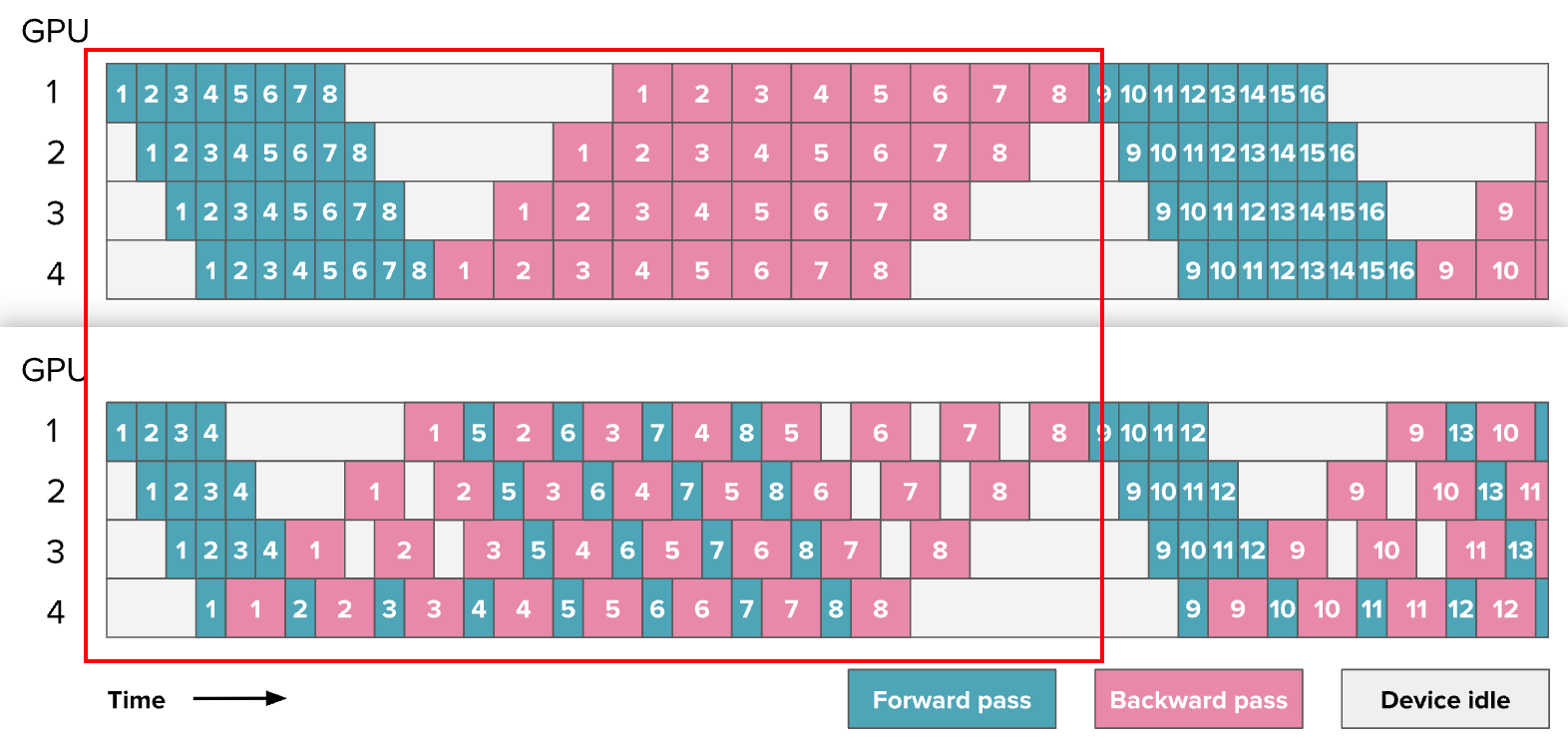
可以发现，修改前后并没有提高训练效率，气泡仍然保持相同大小。

然而，我们只需要存储 p 次micro batch的激活（其中 p 是流水线并行度），而不是 m（其中 m 是Micro Batch数），这可以减少在 AFAB 计划中遇到的激活内存爆炸问题。因此，可以添加更多的微Batch，这实际上会减少气泡。

这种设置的复杂性（如上图所示）主要在于前向和反向传播不再是完全顺序执行的，而是在设备之间并行交错执行。这意味着，需要在每个设备上独立调度从前向传播到反向传播的切换，而不是像往常那样在一个简单的中央训练循环中统一调度。

这也是流水线并行通常需要对训练代码和建模代码进行大幅修改的原因之一。

在 picotron 中找到 1F1B 的完整实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
def train_step_pipeline_1f1b(model, data_loader, tensor_shapes, device, dtype):  
    num_warmup_microbatches = min(pgm.process_group_manager.pp_world_size - pgm.process_group_manager.pp_rank - 1, data_loader.grad_acc_steps)
    num_microbatches_remaining = data_loader.grad_acc_steps - num_warmup_microbatches
    logging_loss, input_tensors, output_tensors  = 0.0, [], []
    requires_grad_sync = pgm.process_group_manager.cp_dp_world_size > 1
  
    def _forward_step(input_tensor):
        batch = next(data_loader)
        batch["hidden_states"] = input_tensor.to(device) if input_tensor is not None else input_tensor
        output_tensor = model.forward(input_ids=batch["input_ids"].to(device), position_ids=batch["position_ids"].to(device), hidden_states=batch["hidden_states"])
  
        # calculate loss on the last stage
        if pgm.process_group_manager.pp_is_last_stage:
            output_tensor = F.cross_entropy(output_tensor.transpose(1, 2), batch["target_ids"].to(device), reduction='mean')
            nonlocal logging_loss
            logging_loss += output_tensor.item() / data_loader.grad_acc_steps
        return output_tensor

    for _ in range(num_warmup_microbatches): # Warmup forward passes
        input_tensor = pipeline_communicate(operation='recv_forward', shapes=tensor_shapes, device=device, dtype=dtype)
        output_tensor = _forward_step(input_tensor)
        pipeline_communicate(operation='send_forward', tensor=output_tensor, device=device, dtype=dtype)
        input_tensors.append(input_tensor)
        output_tensors.append(output_tensor)

    if num_microbatches_remaining > 0:
        input_tensor = pipeline_communicate(operation='recv_forward', shapes=tensor_shapes, device=device, dtype=dtype)
  
    if requires_grad_sync:
        model.require_backward_grad_sync = False

    for ith_microbatch in range(num_microbatches_remaining):  # 1F1B steady state
        is_last_iteration = (ith_microbatch == num_microbatches_remaining - 1)
        output_tensor = _forward_step(input_tensor)
        output_tensor_grad = bidirectional_pipeline_communicate(operation='send_fwd_recv_bwd', send_tensor=output_tensor, recv_shapes=tensor_shapes, device=device, dtype=dtype)
        input_tensors.append(input_tensor)
        output_tensors.append(output_tensor)
        input_tensor, output_tensor = input_tensors.pop(0), output_tensors.pop(0)
  
        # Trigger gradient sync on the last microbatch but only when last rank (the one that has num_warmup_microbatches = 0) has finished computing its backward pass.
        if num_warmup_microbatches == 0 and is_last_iteration:
            model.require_backward_grad_sync = True

        input_tensor_grad = model.backward(input_tensor, output_tensor, output_tensor_grad)
  
        if is_last_iteration:
            input_tensor = None
            pipeline_communicate(operation='send_backward', tensor=input_tensor_grad, device=device, dtype=dtype)
        else:
            input_tensor = bidirectional_pipeline_communicate(operation='send_bwd_recv_fwd', send_tensor=input_tensor_grad, recv_shapes=tensor_shapes, device=device, dtype=dtype)

    for ith_warmup_microbatches in range(num_warmup_microbatches): # Cooldown backward passes
        if requires_grad_sync:
            is_last_iteration = (ith_warmup_microbatches == num_warmup_microbatches - 1)
            model.require_backward_grad_sync = (ith_warmup_microbatches == num_warmup_microbatches - 1)
        input_tensor, output_tensor = input_tensors.pop(0), output_tensors.pop(0)
        output_tensor_grad = pipeline_communicate(operation='recv_backward', shapes=tensor_shapes, device=device, dtype=dtype)
        input_tensor_grad = model.backward(input_tensor, output_tensor, output_tensor_grad)
        pipeline_communicate(operation='send_backward', tensor=input_tensor_grad, device=device, dtype=dtype)

    return logging_loss

来看看 1F1B 流水线并行调度在实践中的扩展情况，并查看集群上的一些基准测试结果：

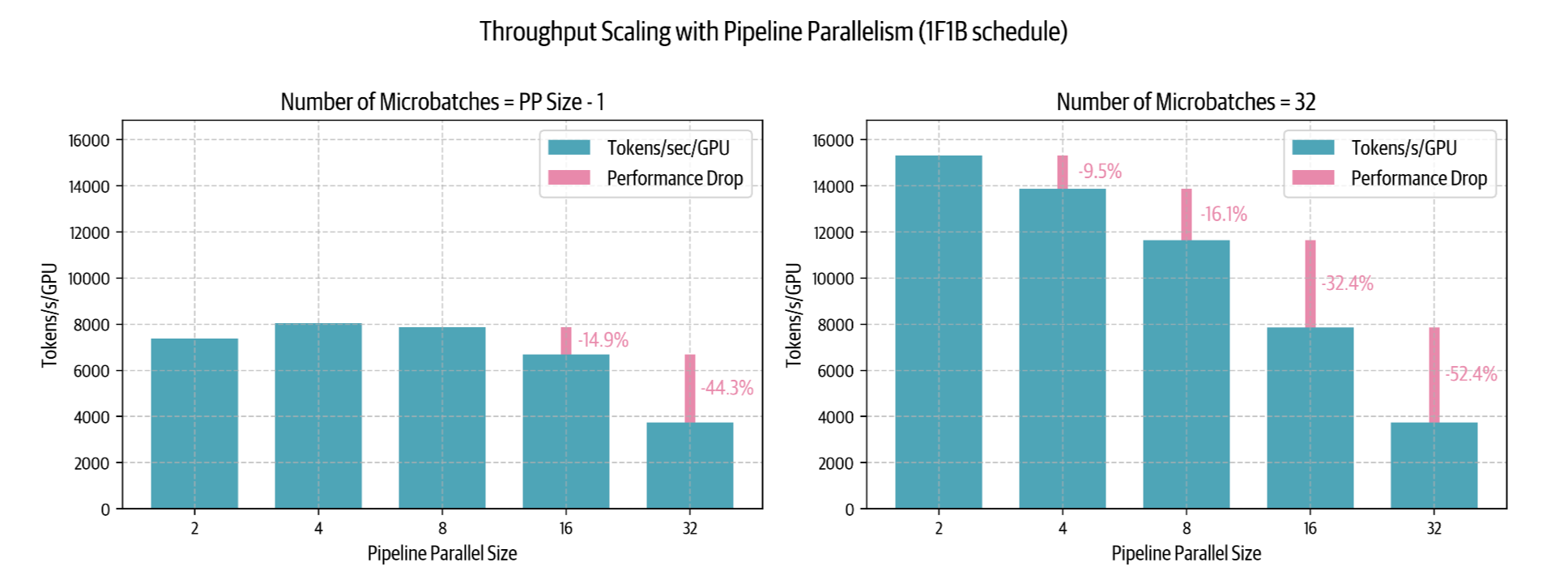
可以观察到：

  • 左侧图表中，当Micro Batch数量等于或小于流水线并行度减1（ $m = p - 1$)时，可以看到流水线气泡的负面影响——性能较低，并且随着流水线并行度的增加甚至下降。
  • 右侧图表显示，当Micro Batch数量远大于流水线并行度（ $m = 32 \gg p - 1$)时，可以改善低并行度时的性能，但在较大并行度时仍然受到限制。实际上，我们无法无限增加Micro-Batch数量以维持 $m \gg p - 1$，因为最终会受限于global batch size。当流水线并行度增加到最大可用Micro-Batch数时，我们将不得不按照 $r_{bubble} = \frac{p-1}{m}$ 增大气泡尺寸。

有趣的是，在较少Micro-Batch的情况下，从一个节点（ $p = 8$)扩展到两个节点（ $p = 16$)时，性能仅下降 14%——这远比张量并行要好，PP在类似的跨节点场景下通常会出现约 43% 的性能下降。这种行为在低带宽跨节点网络环境下，使流水线并行在分布式训练中更具吸引力。

Interleaving Stage 交错阶段

1F1B 调度优化了内存使用，但对于流水线空闲气泡的大小并没有太大改善。有没有更进一步的方法？

事实证明，如果引入一些额外的通信操作，这是可能的。是时候谈谈 交错阶段 Interleaving Stage 了。

到目前为止，按照模型深度对其进行切片，例如，将第 1-4 层放在第一块 GPU 上，将第 5-8 层放在第二块 GPU 上。但其实，可以用不同方式进行切片，例如，将奇数层（1、3、5、7）放在第一块 GPU 上，而偶数层（2、4、6、8）放在第二块 GPU 上。

这本质上形成了一种 “循环流水线 Loop Pipeline”，在前向传播过程中，一个Micro Batch 会在 GPU 之间循环流转。来看一个图示：

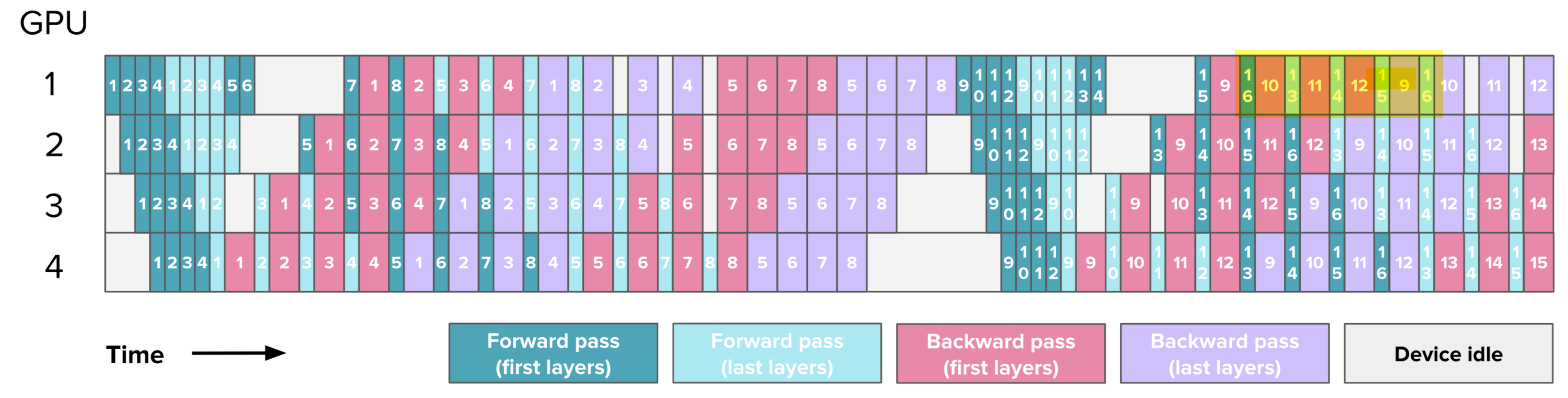
编者注： 深绿色/深红色代表一个模型的前N//2层，浅绿色/浅紫色代表后N//2层。可以看出从1-4卡，前一半和后一半形成交错。在这个例子中$v$=2

随着模型多次通过每个 GPU 进行相同的计算，而之前只需一次遍历，额外的通信发生了。然而，每次正向和反向传播都被除以一个因子 $v$ ,其中 $v$ **是每个 GPU 中的阶段或模型块的数量，因为能够更好地交错正向和反向传播。

因此，可以通过增加Micro-Batch（microbatches）和交错阶段（interleaved stages）来减少流水线气泡（bubble），但需要注意的是，从数量上来看，通信量也会随之增加 $v$，这实际上是一个权衡。在下图中，你可以看到针对

p=8 的流水线并行（PP）设置的几种不同配置，其中 m=1,$v$=1 是最基础的流水线并行方式，而 $v$=1 代表 AFAB 或 1F1B 方案，而 $v$≠1 则是交错配置。

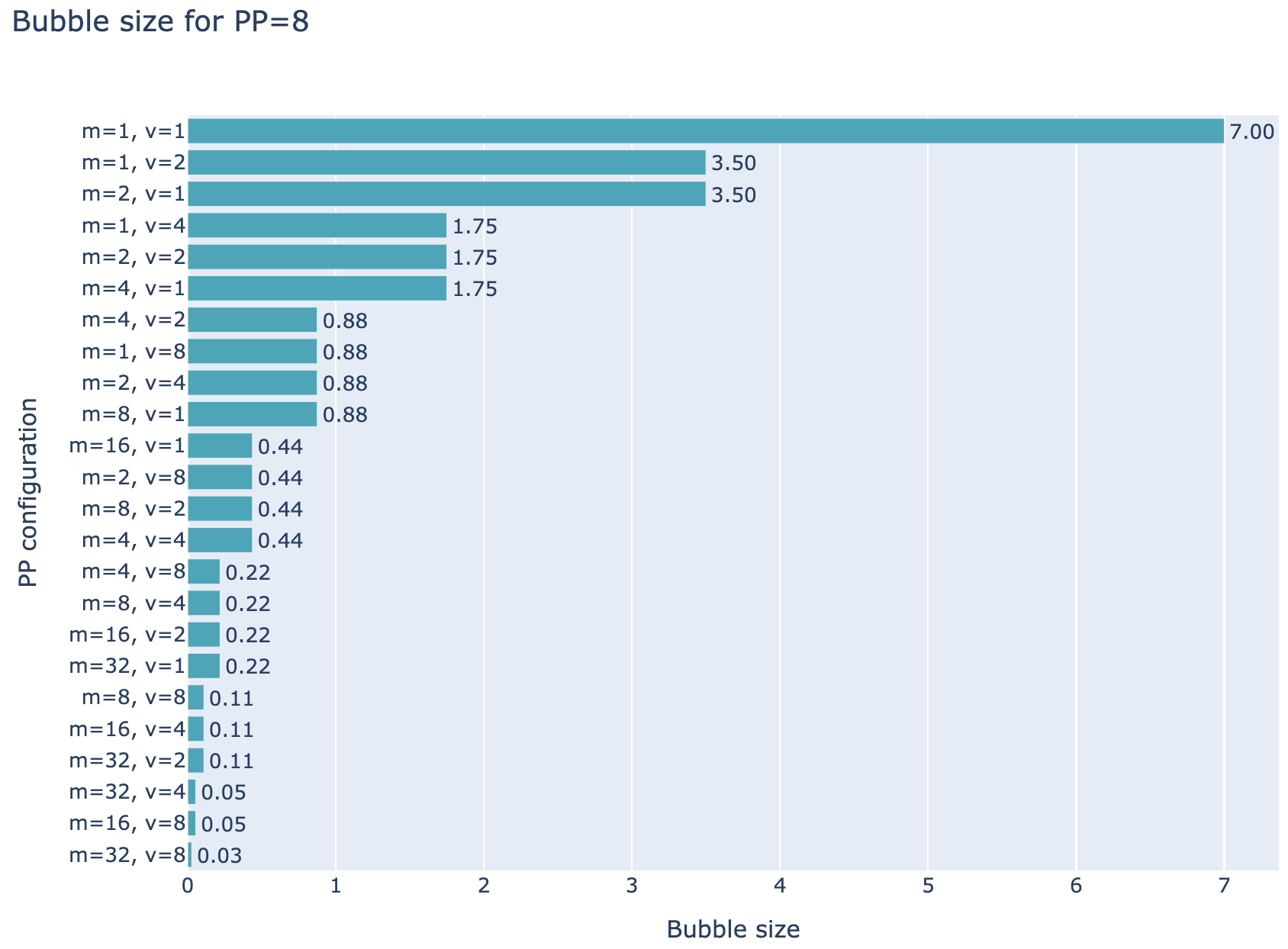
在流水线并行 PP 中，每个 GPU 在某个时刻只能干一件事：要么处理某个Micro-Batch的前向传播（forward pass），要么处理反向传播（backward pass）。因此，需要决定：

  • 是优先让 早期的Micro-Batch（比如 micro-batch 1） 尽快通过所有层，完成前向和反向传播（即尽早“出结果”）？

    举例：

    • GPU 0 处理 micro-batch 1 的第 1-8 层（前向传播）。
    • GPU 1 马上接手，处理 micro-batch 1 的第 9-16 层。
    • 依此类推，直到 micro-batch 1 跑完所有层的前向传播。
    • 然后反向传播也按同样顺序从后向前完成。
    • 等 micro-batch 1 完全处理完，才开始处理 micro-batch 2。

  • 还是优先让 后期的Micro-Batch（比如 micro-batch 2、3、4） 先通过前面的层，把流水线尽量填满？（详细内容见《Breadth-First Pipeline》[3]）

    举例：

    • GPU 0 先处理 micro-batch 1 的第 1-8 层。
    • GPU 0 紧接着处理 micro-batch 2 的第 1-8 层，而不是等 micro-batch 1 跑到下一阶段。
    • 等 GPU 0 处理完多个Micro-Batch后，GPU 1 再依次接手这些Micro-Batch的第 9-16 层。

这两种选择分别对应 深度优先（Depth-First） 和 广度优先（Breadth-First） 的调度策略。

现在，你已经掌握了 Llama 3.1 的流水线并行PP方法的所有关键要素。它采用了一种“一前一后”（1F1B）设置，并结合了交错阶段，同时优先级可调，可在深度优先和广度优先之间调整, 如下图所示：

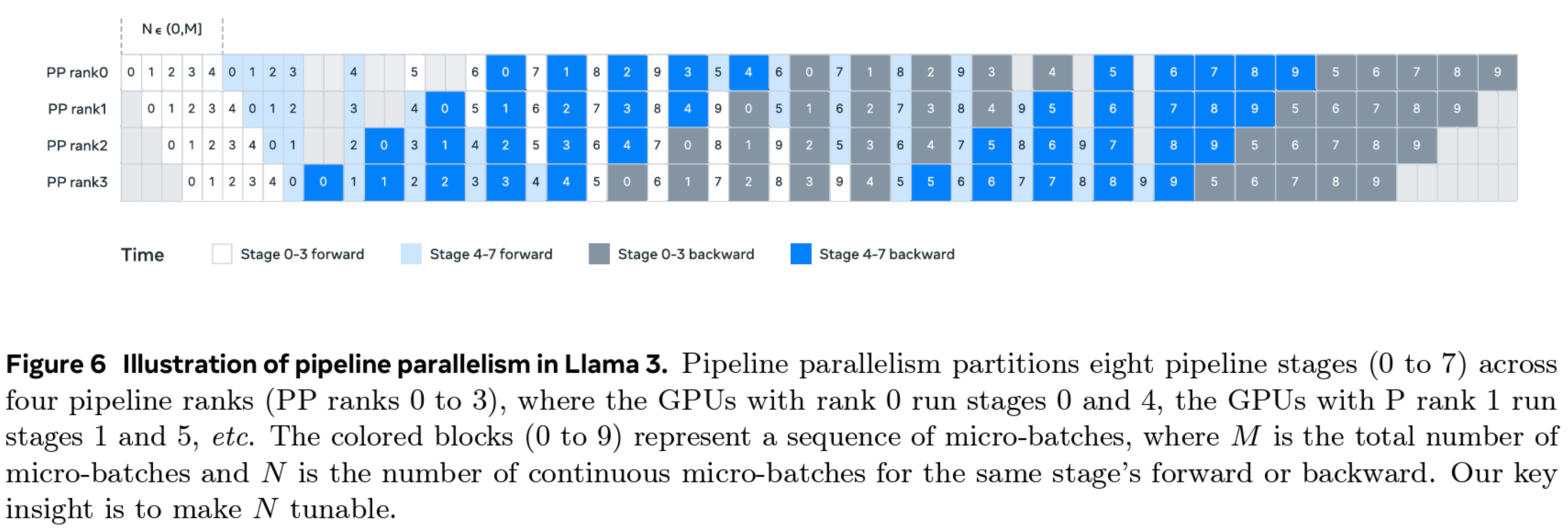
然而，我们尚未探索所有可能的流水线调度方法，最近，一些新方法已经被提出，可以 将气泡减少到几乎为零 ！例如，DeepSeek V3/R1 实现中就使用了这些技术 - DualPipe [4]。是不是很好奇？让在离开流水线并行的世界之前，最后快速看一下这些神奇的调度方法吧！

Zero Bubble & Dual Pipe

最近，一些更复杂的气泡优化方法被提出，并达到了接近“零气泡”的状态。秘诀在于对涉及的操作进行更加精细的拆分，以实现最高效的交错。例如，DeepSeek V3/R1 的流水线实现方法——DualPipe——就几乎达到了零气泡状态。

先简要了解一下 ZeroBubble[5]研究，它是 DualPipe 方法的前身。

ZeroBubble 的核心观察点是：矩阵乘法的反向传播实际上涉及两个独立的操作——输入的反向传播（B）和权重的反向传播（W）：

其中，B（输入的反向传播）的输出对于执行浅层的反向传播是必需的，而 W（权重的反向传播）并不是必须立即执行的，它通常只需要在优化器步骤之前完成。如下图所示：

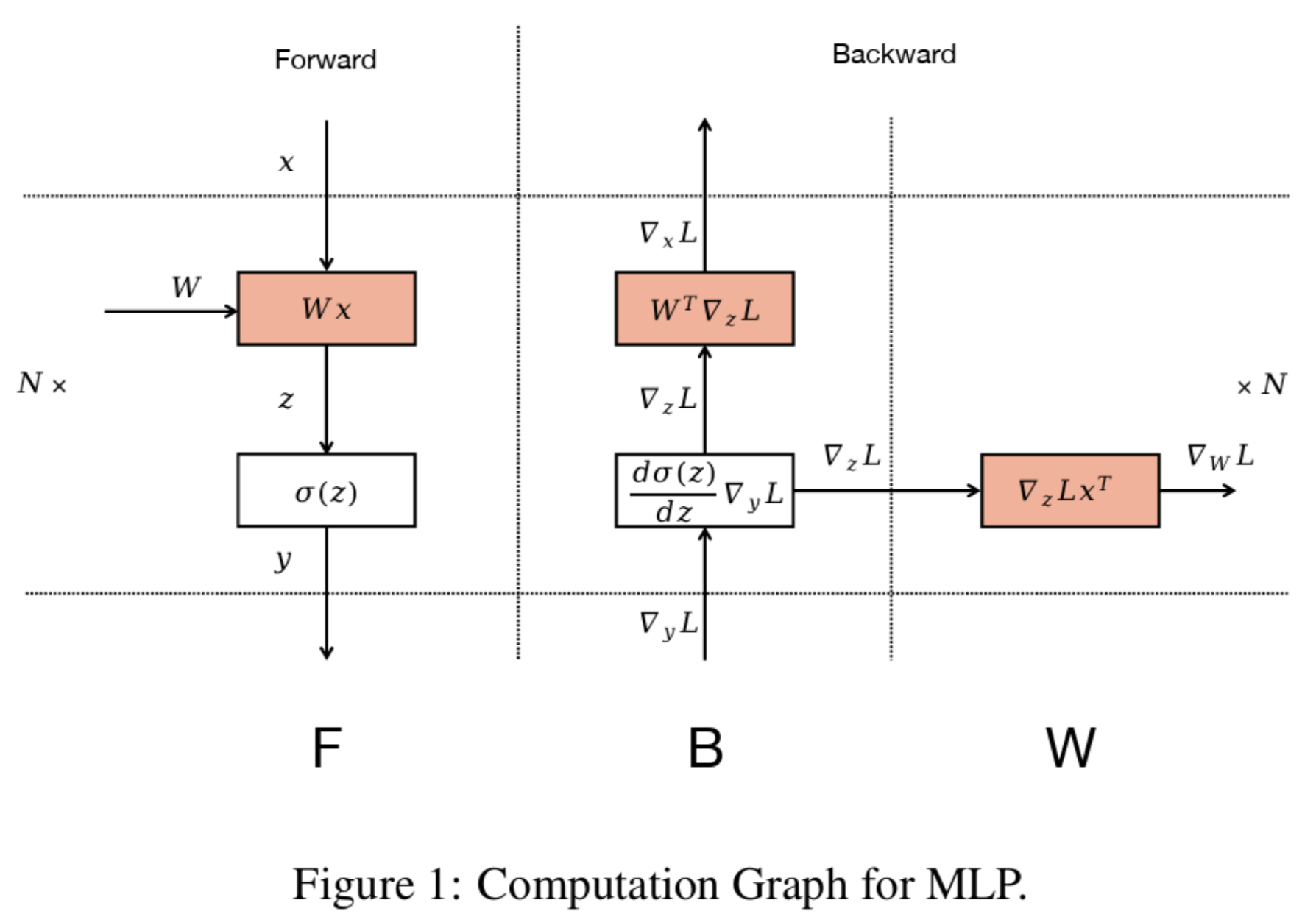
这意味着 W 可以在同一阶段的 B 之后的任何位置灵活调度。这种灵活性使得我们可以巧妙地安排 W，以填补流水线中的气泡。右上角的 ZB-H2 调度就是利用这种精细拆分实现零气泡的示例（理论上的）。

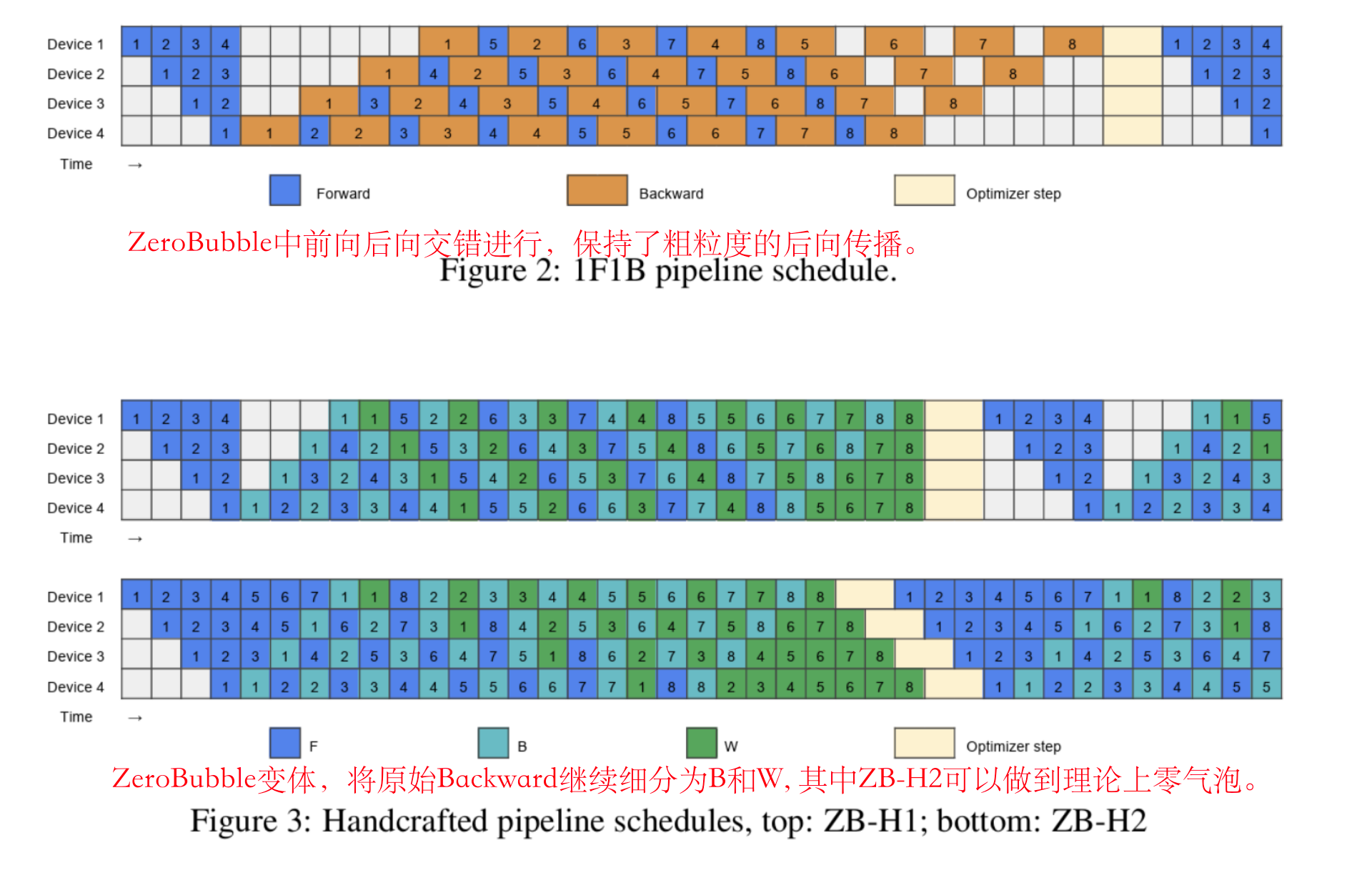
DeepSeekV3中提出的 DualPipe 方法，对这种分解策略进行了扩展，它引入了两个沿流水线并行（PP）维度传播的独立数据流，并通过交错执行来最大限度减少 GPU 的空闲时间。其调度方式如下图所示，比之前的方法更为复杂：

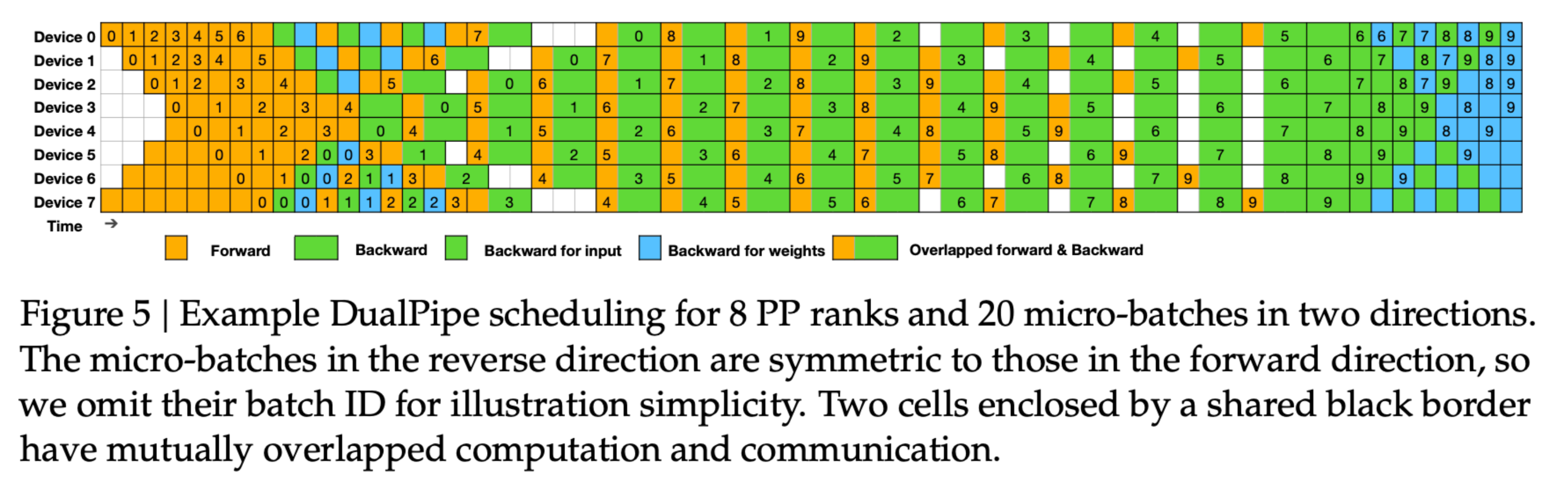
通常，要完全优化如此复杂的调度方式，需要精确测量各个细粒度操作的执行时间，并利用**整数线性规划（ILP）**来最小化最终的气泡时间。ZeroBubble 论文[5] 讨论了用于实现此类调度的启发式方法和算法。因此，ZeroBubble 和 DualPipe 调度方式过于复杂，无法在这里提供代码示例，但你应该已经对其中涉及的概念有了大致了解。

Expert Parallel 专家并行

这是我们要讨论的最后一种并行方法。在深入探讨之前，如果你对专家混合（Mixture-of-Experts，MoE）还不熟悉，可以阅读我们之前发布的博客[6]，它能帮助你更好地理解 MoE 体系结构。

近年来，专家混合模型受到了越来越多的关注，例如 GPT-4、Mixtral，以及最近的 DeepSeek-V3/R1。这类模型的基本思想是，每一层不是单独使用一个前馈模块（feedforward module），而是可以并行使用多个模块，并通过不同的路径处理 token。

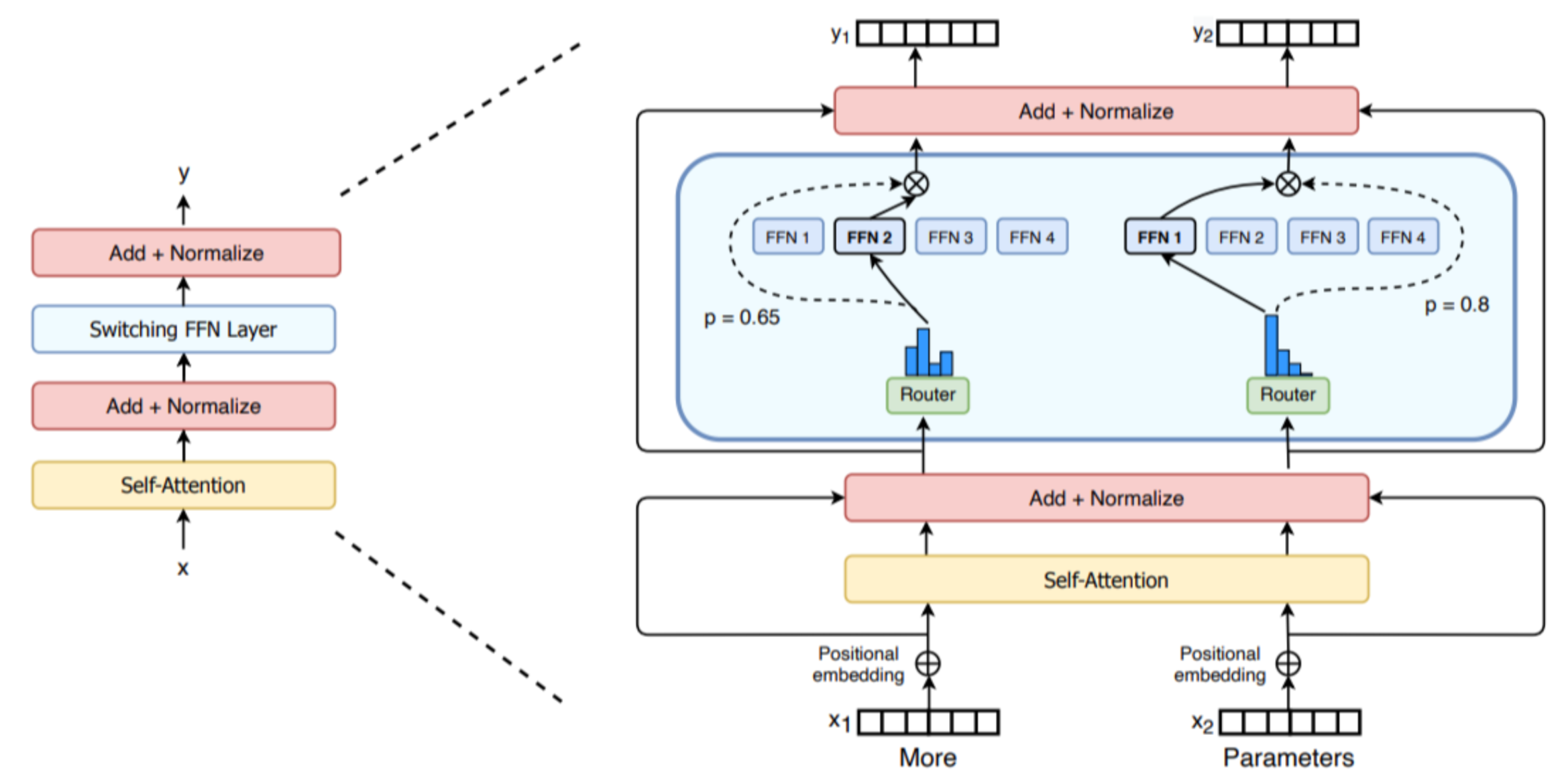
MoE 层的设计使其能够在专家（expert）维度上轻松实现并行计算，称之为 专家并行（Expert Parallelism, EP）。由于前馈层（feedforward layers）完全独立，可以将每个专家的前馈层放置在不同的计算节点上。相比于张量并行（TP），EP 更加轻量级，因为它不需要拆分矩阵乘法，只需要将 token 的隐藏状态正确路由到相应的专家即可。

在实际应用中，EP 通常会与其他并行方式结合使用，例如 数据并行（Data Parallelism, DP）。这是因为 EP 仅影响 MoE 层，并不会像上下文并行（Context Parallelism）那样在序列长度维度上对 token 进行分片。如果仅使用 EP，GPU 仍然会对所有非 MoE 模块执行冗余计算。通过将 EP 与 DP 结合，可以有效地在 GPU 之间分片专家模块和输入Batch，如下图所示：

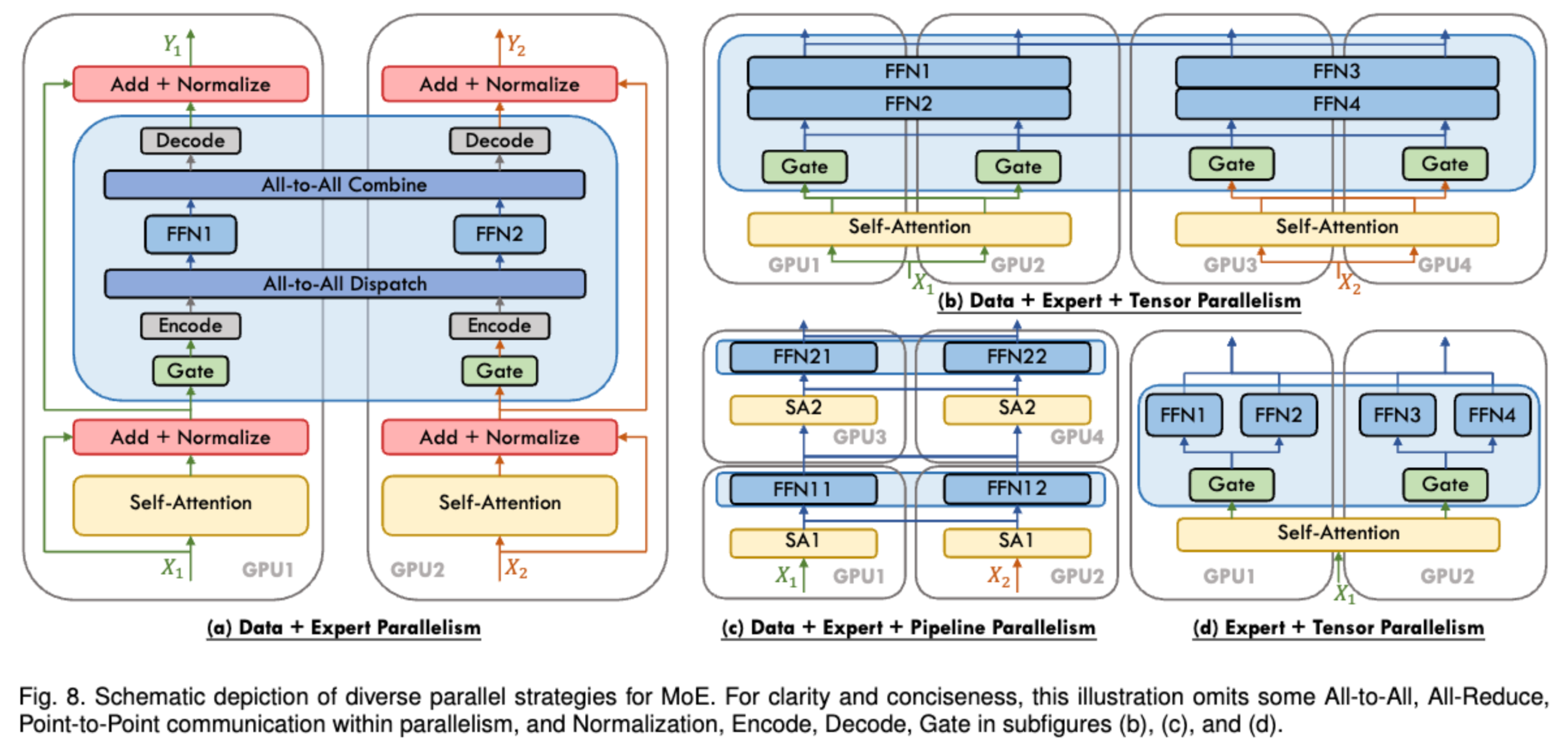
在实践中，有一些技巧可以提高 EP 的效率，这些技巧与模型设计密切相关。例如，DeepSeek-V3 在 router 中施加了一个约束，确保每个 token 最多被发送到 M 个计算节点（在其设计中为 4 个），从而尽可能让 token 保持在单个节点上，并减少通信开销。虽然专家并行已经存在了一段时间, 它现在正随着 MoE 架构的吸引力增强而获得新的动力。

编者注：DeepSeek-V3模型采用混合并行（Hybrid Parallelism）策略，结合了16PP+8TP+Zero-1 DP+64EP, 在8个节点上计算。DualPipe允许同时计算两个连续的流水线阶段。通过重叠这些阶段的计算，可以减少流水线中的空闲时间（bubble），从而提升整体吞吐量

5D Parallelism 5D并行

恭喜你！你已经了解了用于扩展模型训练的五种并行策略：

  1. 数据并行（DP）——按Batch维度并行
  2. 张量并行（TP）——按隐藏维度并行
  3. 序列并行 & 上下文并行（SP/CP）——按序列维度并行
  4. 流水线并行（PP）——按模型层并行
  5. 专家并行（EP）——按模型专家并行

此外，还有三种 ZeRO 策略可以与数据并行结合，以减少内存占用：

  1. ZeRO-1 —— 在 DP 复制之间分片优化器状态
  2. ZeRO-2 —— 在 DP 复制之间分片优化器状态和梯度
  3. ZeRO-3 —— 在 DP 复制之间分片优化器状态、梯度和模型参数

到目前为止，你可能会好奇这些并行和 ZeRO 策略如何相互比较和交互。换句话说，我们应该选择哪些策略进行组合，而哪些应该避免混用？

接下来，我们将分析它们之间的相似性和相互作用。首先，我们将比较流水线并行（PP）和 ZeRO-3，它们在某些方面非常相似，但也存在重要的区别。

(1) 流水线并行 vs. ZeRO-3 —— PP 和 ZeRO-3 都是通过将模型权重分布在多个 GPU 上，并在模型深度轴上进行计算和通信（例如，在 ZeRO-3 中，我们在计算时预取下一层数据）。在这两种方法中，每个设备都需要完整地计算层操作，而不像 TP 或 EP 那样在子层级别进行计算。

ZeRO-3 流水线并行（PP）
每个计算单元存储 仅存储部分层参数 存储完整层参数
通信用于传输 模型权重 激活值
调度方式 与模型无关 与模型无关
实现挑战 模型分片与通信复杂 流水线调度复杂
扩展性 偏好较大 mbs 和 seq_len 以隐藏通信 偏好较大 grad_acc 以隐藏计算空档

正如上表所示，ZeRO-3 和 PP 解决了相同的挑战，但采用了不同的方法，选择哪种方式取决于你是更关注权重的通信，还是激活的通信。虽然它们可以结合使用，但在实践中不常见，因为这样做需要显著增加global batch size 以摊销通信成本，从而在global batch size、模型大小、网络带宽和训练效率之间形成权衡。如果你决定结合使用它们，ZeRO-3 应该被配置为在一系列 PP Micro Batch 期间将权重保留在内存中，以尽可能减少不必要的通信开销。

另一方面，ZeRO-1 和 ZeRO-2 关注优化器状态和梯度，它们可以轻松与流水线并行（Pipeline Parallelism）结合，并且是互补的。结合使用它们不会带来额外的新挑战。例如，DeepSeek-v3 的训练使用了 PP 结合 ZeRO-1。

(2) 张量并行（Tensor Parallelism）与序列并行（Sequence Parallelism）是天然互补的，并且可以与流水线并行 PP 和 ZeRO-3 结合使用，因为它依赖矩阵乘法的分布性质，使得权重和激活可以被分片并独立计算后再合并。

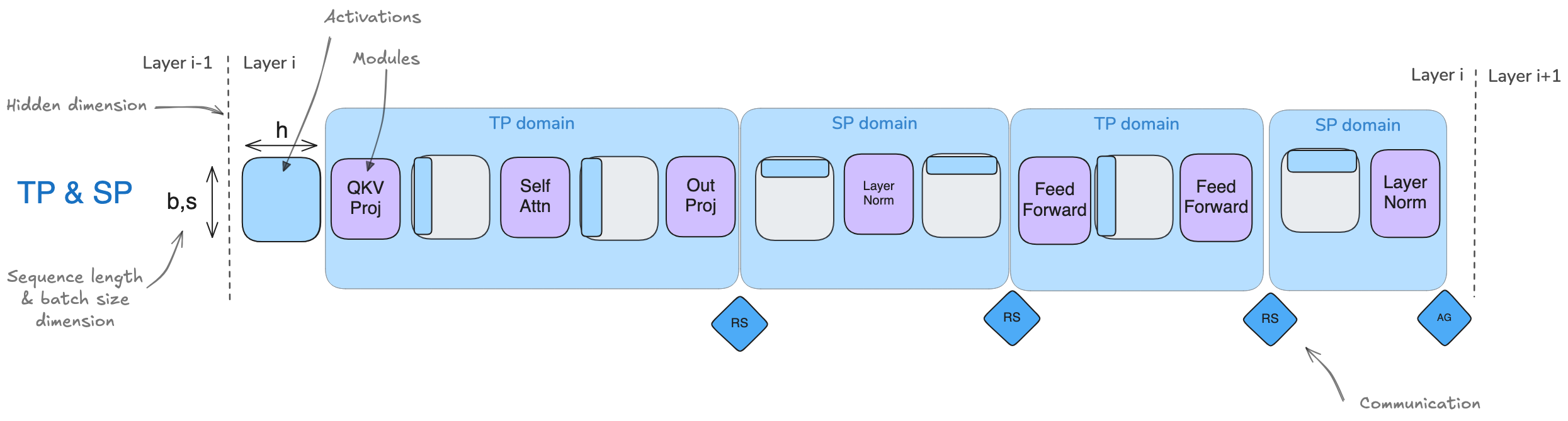
我们不希望仅使用 TP 进行并行计算的主要原因是，在实践中，TP 有两个限制，在前面部分已经讨论过：

  • 首先，由于其通信操作是计算的关键路径之一，在扩展到一定规模后，通信开销开始占据主导地位，使得扩展变得困难。
  • 其次，与 ZeRO 和 PP 这类与模型无关的方法不同，TP 需要仔细处理激活分片——有时沿隐藏维度（TP 区域），有时沿序列维度（SP 区域）——这使得其正确实现变得更加复杂，并且需要特定的模型知识来确保整个过程中分片模式的正确性。

因此，在结合并行策略时，TP 通常用于高速的节点内通信，而 ZeRO-3 或 PP 则用于跨节点的低速通信，因为它们的通信模式对带宽需求较低（PP），或者更容易与计算重叠（ZeRO-3）。

结合这些技术时，主要的考虑因素是如何高效地组织 GPU，使其在每个并行维度的分组中最大化吞吐量并最小化通信开销，同时注意 TP 的扩展限制。例如，TP 的通信 GPU 组应保持在同一个节点内部

(3)上下文并行（Context Parallelism） 和 专家并行（Expert Parallelism） 也可以帮助分片激活，并且可以视为 TP 的补充。前者处理长序列，而后者用于分布式 MoE 训练，它们可以无缝结合使用。

上下文并行（CP） 主要用于解决超长序列训练的挑战，它通过在 GPU 之间沿序列维度分片激活来实现。大多数操作（如 MLP 和 LayerNorm）可以独立处理这些分片的序列，而注意力层需要通信，因为每个 token 需要访问整个序列的 key/value。通过环形注意力模式（ring attention patterns）高效地处理，实现了计算和通信的重叠。当扩展到极端长的序列（128k+ tokens）时，即使使用完整的激活重计算，单个 GPU 也无法满足注意力计算的内存需求，此时 CP 就尤为重要。

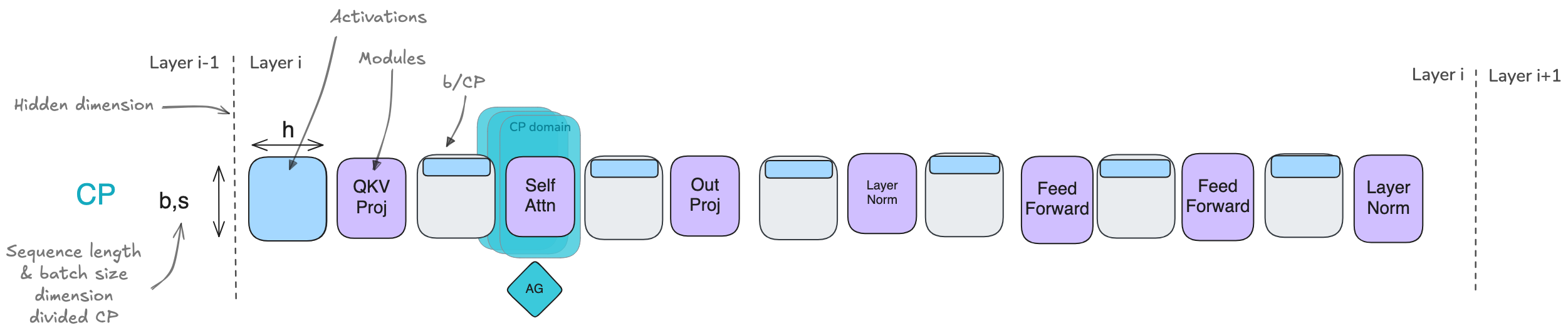
(4) 专家并行（EP） 主要用于训练 MoE（Mixture of Experts）模型，它通过在 GPU 之间分片专门的“专家”（experts），并在计算过程中动态地将 token 路由到相关的专家。EP 中的关键通信操作是 all-to-all 操作，它负责将 token 发送到相应的专家，并收集返回的计算结果。虽然这种操作引入了一定的通信开销，但它使得模型容量可以大规模扩展，因为每个 token 在推理（或训练）期间仅由一小部分参数处理。对于大规模专家模型，将专家在 GPU 之间分片变得尤为重要。

备注：

EP 在输入处理方面与数据并行（DP）有相似之处，因此某些实现将专家并行视为数据并行的一个子类别，主要区别在于 EP 使用专门的专家路由，而不是让所有 GPU 处理相同的模型副本。

范围与重点 我们快速总结一下不同的并行策略在模型的哪些部分影响最大：

  • 张量并行TP和序列并行SP影响整个模型的计算，它们分片权重和激活。
  • 上下文并行CP主要影响注意力层，因为这里需要跨序列通信，而其他层可以独立处理分片的序列。
  • 专家并行EP主要影响 MoE 层（替代标准的 MLP 块），不会影响注意力和其他组件。
  • 流水线并行PP和 ZeRO 并不特别针对某个子模块或组件，但在流水线并行中，模块和层需要均衡分布，第一层和最后一层通常需要特殊处理，因为它们涉及额外的嵌入层。
张量 + 序列并行 上下文并行 专家并行
沿隐藏/序列维度分片权重和激活 沿序列维度分片激活 分片专家权重和激活
用于矩阵乘操作的通信（列/行线性） 注意力键/值的通信 用于专家路由的通信
需要特定于模型的实现 除了注意力外都是通用的 除了MoE层外都是通用的
偏好高带宽的节点内通信 偏好大序列长度 需要MoE

总结一切—— 现在，让我们尝试将我们在一个单一图表中看到的所有技术聚合和组合起来。

在这个总结图表中，你将找到单个transformers层的激活和模块的插图，以其MoE变体形式展示。我们还展示了各种并行性的方向以及我们在所有前文讨论中讨论过的通信操作。

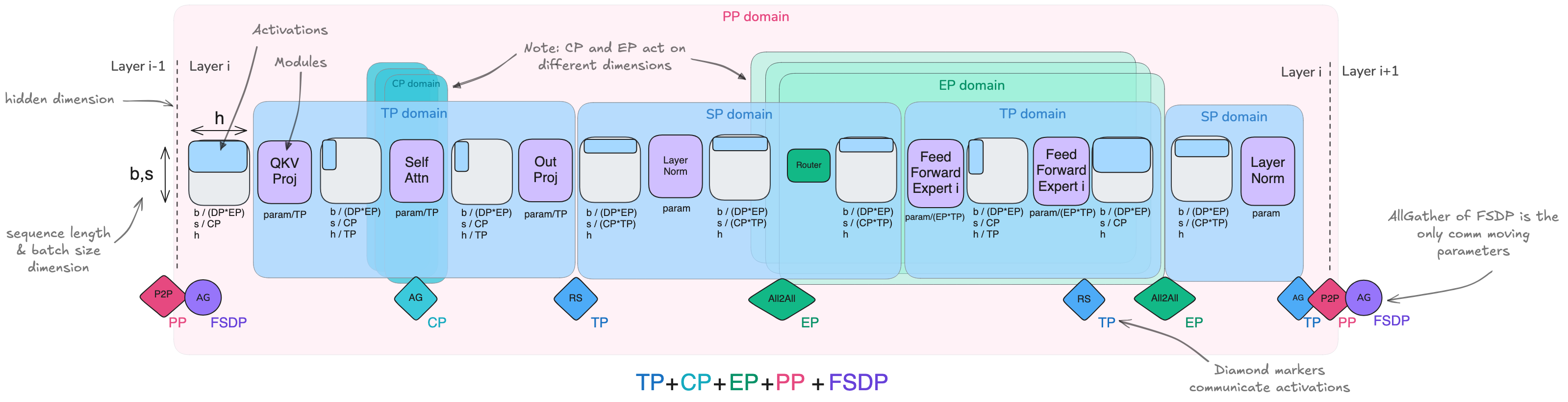
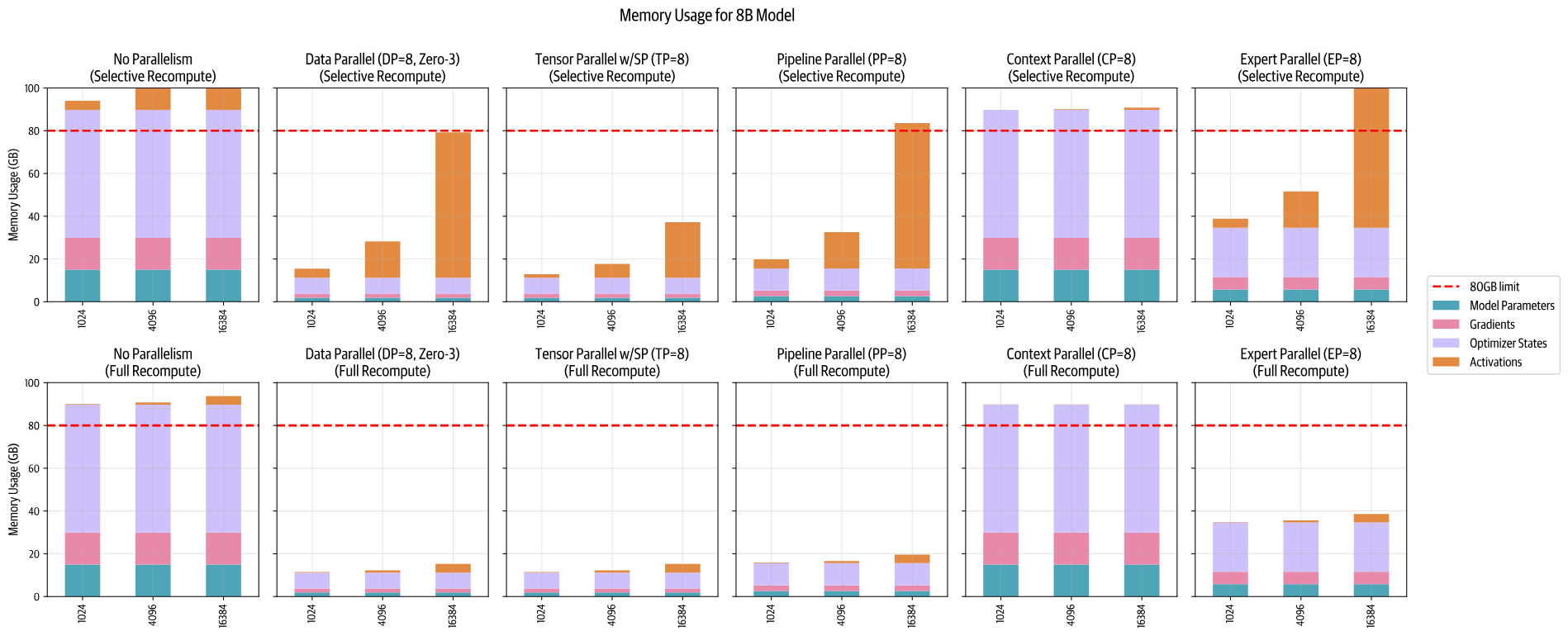
我们还可以并排表示这些策略的全面概述。我们将它们与不同的序列长度以及（顶部） Selective 和（底部） Full Recomputation 一起绘制，以便你了解它们如何与激活交互：

让我们以一个高层次的视角结束本节，看看所有这些技术，它们的主要基本思想和主要瓶颈：

方法 特定应用的内存节省 并行/分片维度 缺点
数据并行（DP） 激活（减少Local BS） Batch 受最大Batch大小限制
管道并行（PP） 模型参数 模型层 空闲周期和复杂调度
张量/序列并行（TP/SP） 模型参数和激活 隐藏维度/序列长度 需要高带宽通信
上下文并行（CP） 激活 序列长度 在注意力模块中增加通信开销
专家并行（EP） 专家参数 专家维度 需要MoE层，增加路由通信开销
ZeRO-1 优化器状态 分片在DP复制中 参数通信开销
ZeRO-2 优化器状态和梯度 分片在DP复制中 参数通信开销
ZeRO-3 优化器状态、梯度和模型参数 分片在DP复制中 参数通信开销

显然，这些技术都不是解决所有问题的灵丹妙药，我们经常需要以某种方式组合它们。我们是否可以制定一些规则，帮助我们找到选择和组合它们的良好起点？这将是我们下一节的主题。

参考文献

[1] https://huggingface.co/spaces/nanotron/ultrascale-playbook

[2] https://huggingface.co/spaces/Ki-Seki/ultrascale-playbook-zh-cn

[3] Breadth-First Pipeline Parallelism

[4] DeepSeek-V3 Technical Report https://arxiv.org/pdf/2412.19437

[5] Zero Bubble Pipeline Parallelism https://arxiv.org/pdf/2401.10241

[6] https://huggingface.co/blog/zh/moe

寻找最佳训练配置

目前已经讨论了所有实际用于分发和训练大型模型的并行技术，以及它们如何以及为什么可以组合在一起。现在还有一个普遍问题：最终我们应该选择哪些技术，以及如何决定具体的组合方式？

我们在前一节中稍微提到了这个问题，但现在详细地走一遍可能的决策过程，逐步进行，记住我们需要运行一些实验，以找到适合给定计算集群的最终最优设置，考虑其各种物理特性、网络带宽、每个节点的GPU数、每个GPU的内存等。

步骤1：将模型放入到Memory中 - Model Size维度

首先，我们需要弄清楚如何将完整的模型实例适配到GPU上。一般有两种情况。

GPU丰富情况 - 当你有大量GPU可用时：

  • 对于小于10B参数的模型，可以使用单一的并行技术，例如张量并行TP或ZeRO-3/DP结合在8个GPU上进行完整重计算
  • 对于需要超过8个GPU的10B-100B参数模型，你有几个选项：
    • 结合张量并行（TP=8）和流水线并行（PP）
    • 结合张量并行（TP=8）和数据并行（ZeRO-3）
    • 仅使用ZeRO-3（即纯粹的数据并行）
  • 在512+ GPU规模下，纯DP/ZeRO-3由于通信成本开始变得低效 - 在这种情况下，结合DP与TP或PP可能更好
  • 在1024+ GPU规模下，推荐的设置可以是张量并行TP=8与DP（ZeRO-2）和流水线并行PP结合

特殊情况：

  • 对于非常长的序列，可能需要跨节点使用上下文并行（CP）。
  • 对于专家混合体系结构，将优先使用跨节点的专家并行（EP）。

GPU资源匮乏情况 - 当你的GPU资源可能不足时：

  • 可以启用完全的Activation Recomputation，用计算来换空间，但是这会导致训练速度变慢。
  • 可以增加梯度累积 Gradient Accumulation 中的Micro Batch 以处理具有有限内存的更大批次。

现在我们已经有了第一个模型实例进行训练，那么如何正确的设置batch size?

步骤2：实现目标Global Batch Size - BS维度

根据步骤1中Micro Batch和DP，当前的BS可能太小或太大。如何达到target batch size?

为了增加当前的Global Batch Size：

  • 可以扩展数据并行DP或梯度积累Gradient Accumulation步骤
  • 对于长序列，我们可以利用上下文并行 CP

为了减少当前的Global Batch Size：

  • 可以减少数据并行DP，转而支持其他并行策略
  • 对于长序列，可以减少上下文并行 CP

好的，现在我们的模型在模型大小和Batch Size方面运行在我们想要的一般配置下，但我们是否正在以最快的方式训练它？现在让我们尽可能地开始优化吞吐量。

步骤3：优化训练吞吐量 （Throughput维度）

我们希望确保训练尽可能快速，以便我们所有宝贵的GPU在任何时候都能得到充分利用。只要内存和通信不是瓶颈，我们可以尝试以下方法：

  • 扩展张量并行 TP（利用快速的节点内带宽），直到接近节点大小，以便减少其他并行性。
  • 增加数据并行 DP 与ZeRO-3，同时保持Target Batch Size
  • 当数据并行 DP 通信开始成为瓶颈时，过渡到使用流水线并行 PP
  • 逐个尝试扩展不同的并行策略
  • 尝试几种 Micro Batch（MBS），以寻求最大GBS、模型大小、计算和通信之间的最佳平衡。

成千上万个配置的基准测试

现在我们已经详细介绍了每一步，让我们将这个搜索过程应用于现实中。

你将在 nanotron 仓库[1]中找到几个脚本，可以用来运行我们上述讨论的所有实验，并能够在实际基准测试你自己的模型和集群。

我们实际上对数千种分布式配置进行了自我基准测试，涵盖了上述讨论的所有模型大小，以及能够尝试的非常大量的集群配置（即 8xH100s 的 1-64 个节点），可以用来复现本书中的结果。

现在汇总和分析我们所有基准测试的结果，看看除了理论之外，是否可以在真实数据上发现各种配置彼此之间的差异。

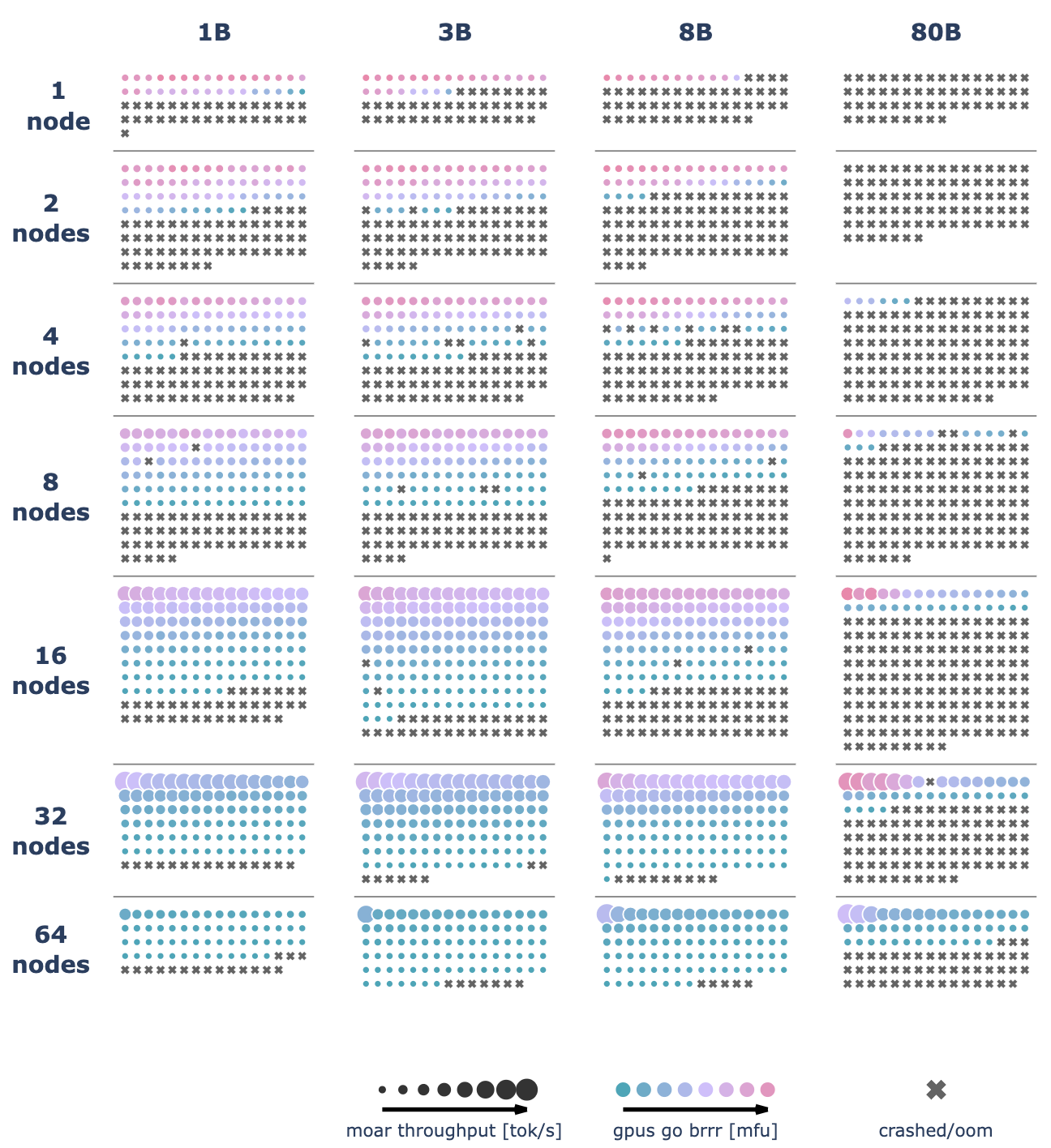
所有以下基准测试均以序列长度为4096和Global Batch Size为1M tokens进行。我们收集了每个模型和集群大小的最佳配置，并在以下热图中进行了展示：

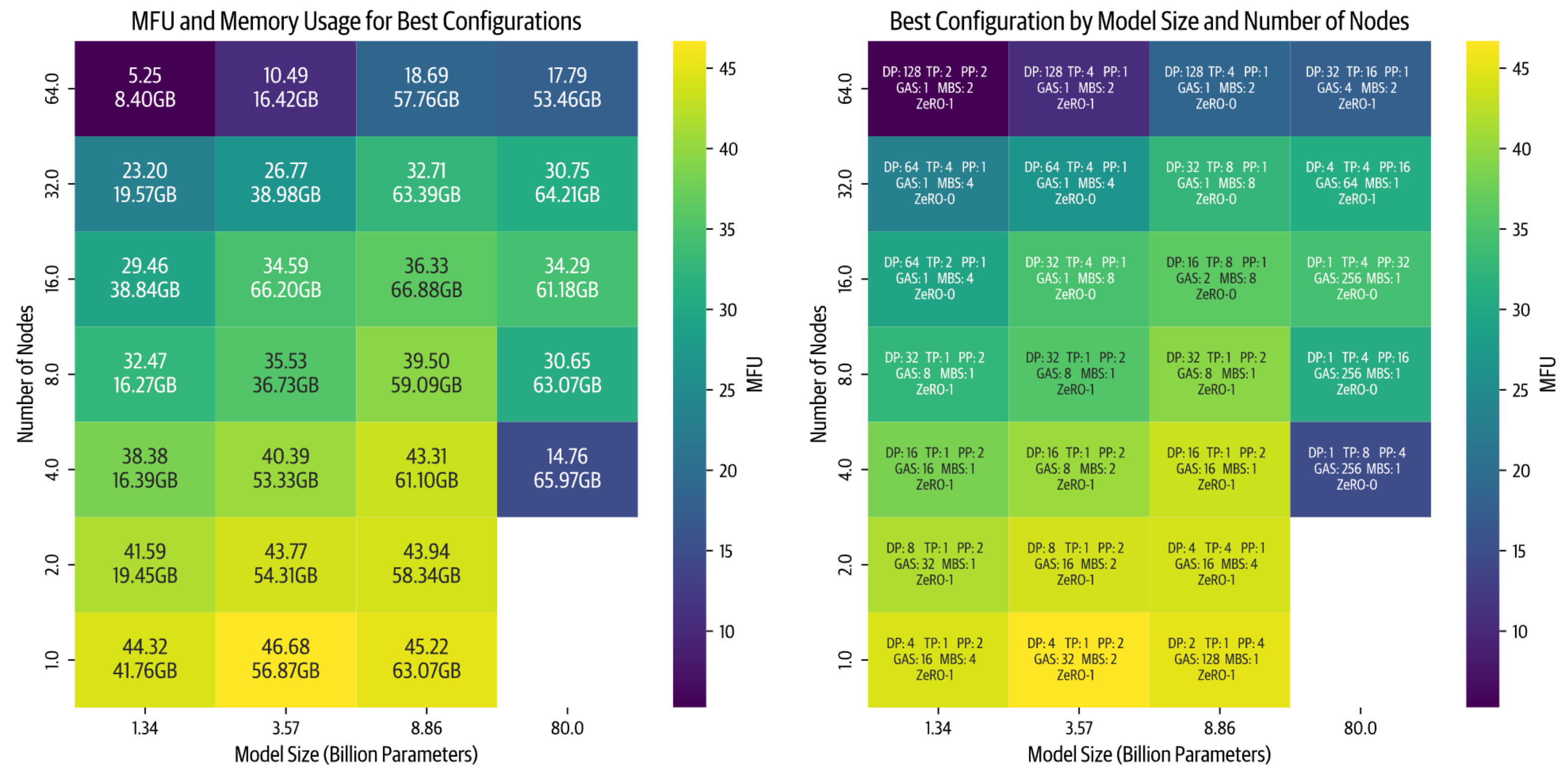
编者注： GAS: Gradient Accumulation Steps; MBS: Micro Batch Size; MFU: Model FLOPs Utilization； 这张图非常宝贵，因为我们可以直接用来查询显存使用情况，比如当前有一个Node，我希望训练一个8B的模型，那么可以通过上图查询得到每张卡至少需要63GB显存，并且最优配置给出了，DP2 TP1 PP4 GAS128 Zero-1。

通过这个高级别的可视化，我们可以得出几个重要的insight：

  • 随着节点数量的增加（更高的并行性），效率会下降。这种效果在较小的模型中尤为显著，因为其计算与模型大小比例较低。虽然通常可以通过增加批次大小来补偿小模型大小，但我们受到全局批次大小 GBS 限制 1M 的约束。
  • 较大的模型表现出了不同的挑战。随着模型大小的增加，内存需求显著增加。这导致了两种情况在较少节点时出现：
    • 要么模型根本不适合 （上图右下角空白处）
    • 要么几乎适合但由于接近GPU内存限制而运行效率低下（例如在 4 个节点上训练 80B 参数模型）。

最后，基准测试显示性能严重依赖于实现质量。当首次实施两种并行策略时，张量并行（TP）优于流水线并行（PP）。在优化了PP代码之后，它成为了更快的选项。现在我们正在改进TP实现中的通信重叠，预计它将重新获得性能优势。

基准测试中的经验教训

我们对本书的目标不仅仅是讨论理论和实现，还提供实际数据点。因此，计划很简单：运行每种模型的每种可能的分布式配置，以及多个集群大小（即每个节点8xH100的1-64个节点）。即使排除了不可能的配置，我们仍然需要运行数千次实验。

这听起来足够简单：我们可以在集群上轻松启动大量作业。然而，一旦我们启动了第一批实验，问题就开始出现：

  • PyTorch进程有时无法正确清理
  • Slurm作业管理器会强制终止作业，导致节点故障
  • 本应只需几分钟的简单基准测试变成了几个小时
  • 有些作业会无限期挂起

在有限的时间内运行所有实验需要额外的工程设计，最终花费了大量时间处理诸如：

  • 最小化集群重启时间并优化空闲时间
  • 分析详细的NCCL调试日志
  • 了解内存使用模式和CUDA内存分配器行为
  • 改进多节点上的流水线并行性能

这些挑战值得分享，但它们教会了我们有关分布式训练基础设施复杂性的宝贵教训。理论上看起来简单的东西，在实践中往往需要对许多运作部件进行仔细关注。

在实践中复现理论结果是具有挑战性的，特别是由于生产训练代码的有限可用性。通过像 nanotron 和 picotron 这样的开源项目，我们希望能够帮助使分布式训练技术更加可访问，并在简单高效的代码库上进行合作，帮助研究人员和从业者充分利用他们的硬件资源。

到这里，这结束了我们对5D并行方法分布的深入探讨。

回顾我们迄今为止的讨论，我们的许多讨论都依赖于一个关键假设 - 即可以在GPU上有效地重叠计算和通信，而不会对计算吞吐量产生影响。现实情况更加微妙。当使用像NCCL send/recv这样的常见通信原语时，我们面临计算资源和通信资源之间的隐藏竞争，因为通信核心通常会使用相同的GPU流处理器（SM），这些SM用于计算，导致在通信与计算重叠时吞吐量降低。要真正优化分布式训练，需要更深入地了解GPU架构本身。

参考文献

[1] https://github.com/huggingface/nanotron

[2] https://github.com/huggingface/picotron

GPU 深度挖掘——融合、线程化、混合

截至目前，我们的讨论主要集中在模型操作的high-level组织结构上。我们已经在不同加速器上关注了计算，同时考虑到一般内存限制和计算单元的高级调度。

但这忽略了我们可以在更低层次上通过仔细理解我们的模型操作如何在每个GPU上调度和执行来做的所有优化。

本节将深入介绍GPU架构的更多细节，特别是NVIDIA的GPU架构，但通常的想法可以在类似的加速器单元上重复使用。

在覆盖Flash-Attention革命如何有效调度GPU工作负载之前，我们将简要解释GPU的组织方式，并最终解释如何在GPU上有效使用各种精度。

GPU入门

通常，GPU 具有非常层次化的组织结构。在本指南中，我们将保持讨论在支撑我们后续展示所需的概念层面。

(1)在计算方面，GPU由一组称为流多处理器 Streaming Multiprocessors（SM）的计算单元组成并控制。每个SM包含并控制一组流处理器，也称为核心 Cores。例如，Nvidia H100 GPU具有132个SM，每个SM有128个核心，总共有16,896个核心（有关张量核心的详细信息，请参见[张量核心文档]https://resources.nvidia.com/en-us-tensor-core），每个核心可以同时处理多个线程 Thread。

编者注：计算分层概念： SM → Core → Thread
实际编程概念：SM → Grid → Block → Thread Warps(线程束）→ Thread

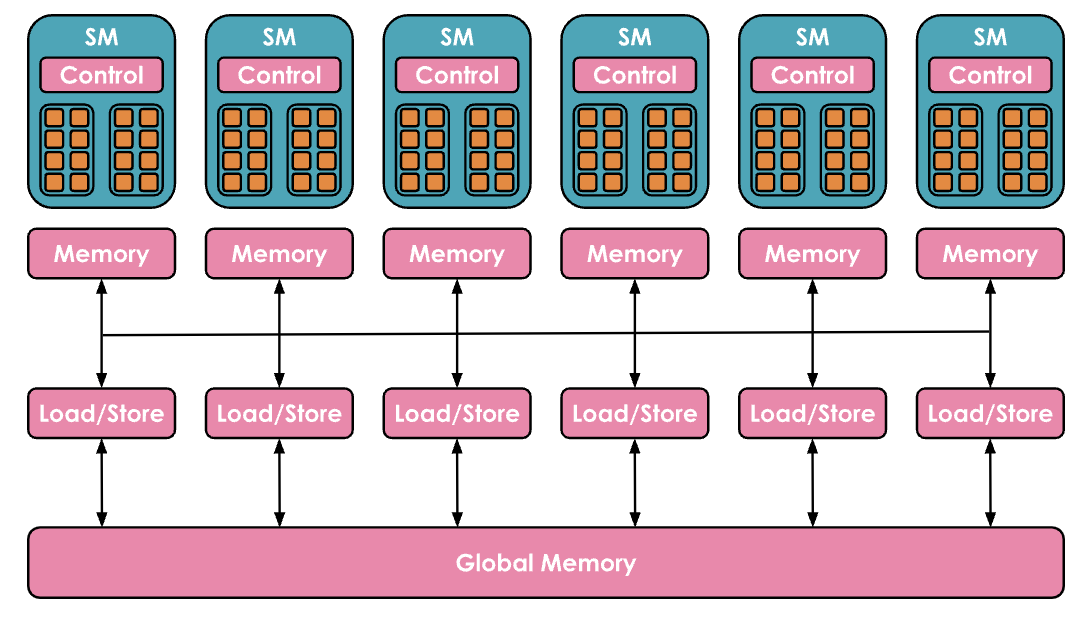
(2)内存方面也高度分层，具有多层缓存和内存：寄存器 Registers 是最小的单位，在执行过程中是私有的，共享内存 Shared Memory 和 L1 Cache在单个SM上运行的线程之间共享，更高层次是所有SM共享的L2缓存 Cache，最后是全局内存 Global Memory，这是GPU上最大的内存（例如H100的80GB），但访问和查询速度也是最慢的。

编者注：内存分层：Global Mem → L2 Cache → L1 Cache → Shared Mem

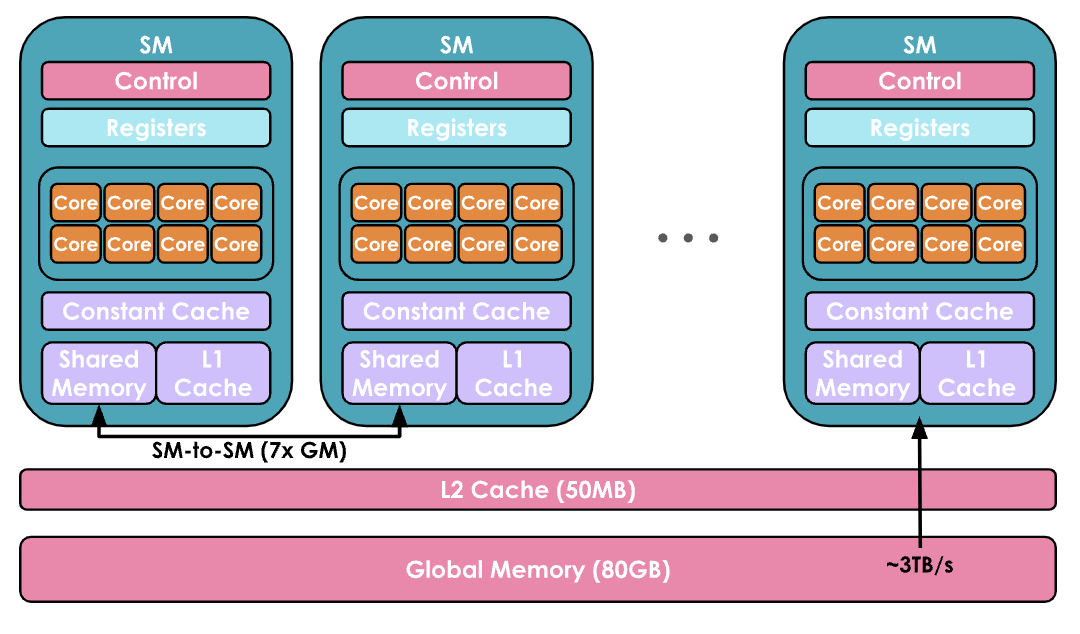
GPU的目标是通过利用计算/内存的这种分层组织，尽可能并行地在GPU核心上运行尽可能多的工作负载。

在GPU核心上运行的代码片段称为内核 Kernel。它可以在高级别上用 CUDA或Triton等语言编写，然后编译为NVIDIA GPU使用的低级汇编 Parallel Thread Execution（PTX）。

要运行内核，你还需要一个特定的代码部分，称为主机代码 Host Code，它在CPU/主机上执行，并负责准备数据分配和加载数据和代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// Host code        
void vecAdd(float* h_A, float *h_B, float *h_c, int n) {
    // Allocate vectors in device memory
    int size = n * sizeof(float);
    float *d_A, *d_B, *d_C;
    cudaMalloc(&d_A, size);
    cudaMalloc(&d_B, size);
    cudaMalloc(&d_C, size);

    // Copy vectors from host memory to device memory
    cudaMemcpy(d_A, h_A, size, cudaMemcpyHostToDevice);
    cudaMemcpy(d_B, h_B, size, cudaMemcpyHostToDevice);

    // Invoke kernel
    int threadsPerBlock = 256;
    int blocksPerGrid =
            (N + threadsPerBlock - 1) / threadsPerBlock;
    VecAdd<<<blocksPerGrid, threadsPerBlock>>>(d_A, d_B, d_C, N);

    // Copy result from device memory to host memory
    // h_C contains the result in host memory
    cudaMemcpy(h_C, d_C, size, cudaMemcpyDeviceToHost);

    // Free device memory
    cudaFree(d_A);
    cudaFree(d_B);
    cudaFree(d_C);
}

内核通常按如下方式调度：

  • 线程被分组成大小为32的线程束（warps）。线程束中的所有线程被同步以同时执行指令，但在数据的不同部分上。
  • 线程束被分组成更大的块（blocks），大小更灵活（例如大小为256），每个块仍然分配给单个SM。一个SM可以并行运行多个块，但是根据资源情况，并非所有块都会立即分配执行，有些可能会等待资源。

从这些细节中最重要的是记住，有各种大小和分配约束（各种内存的大小，每个线程束和块中的线程数），需要考虑使用GPU架构的最有效方式。

大多数情况下，你不需要这么精确，幸运的是，你可以重用社区其他成员准备的内核和代码。但无论如何，我们希望为你提供有关如何开始使用内核的入门指南！

如何用kernel提升性能？

如果你想添加一个缺少优化过的内核的新操作或加快现有的 PyTorch 函数，从头编写内核可能看起来是最直接的方法。然而，从头创建高性能的 CUDA 内核需要丰富的经验和陡峭的学习曲线。通常，更好的入门方法是利用 torch.compile ，它通过捕获你的操作并在 triton 中生成低级、高性能内核来动态优化 PyTorch 代码。

假设你想编写一个名为指数线性单元 ELU 的激活函数的内核：

$$
\text{ELU}(x) = \begin{cases} e^x - 1 & \text{if } x < 0 \ x & \text{if } x \geq 0 \end{cases}
$$

你可以从一个简单的 PyTorch 实现开始，然后只需在顶部添加 @torch.compile 装饰器即可：

1
2
3
@torch.compile
def elu(x, alpha=1.0):
    return torch.where(x < 0, alpha * (torch.exp(x) - 1), x)

编译版和非编译版之间的区别非常明显，尤其是在只添加了一个装饰器的情况下。这种显著的不同在下图中得到了体现（N 表示列数）：

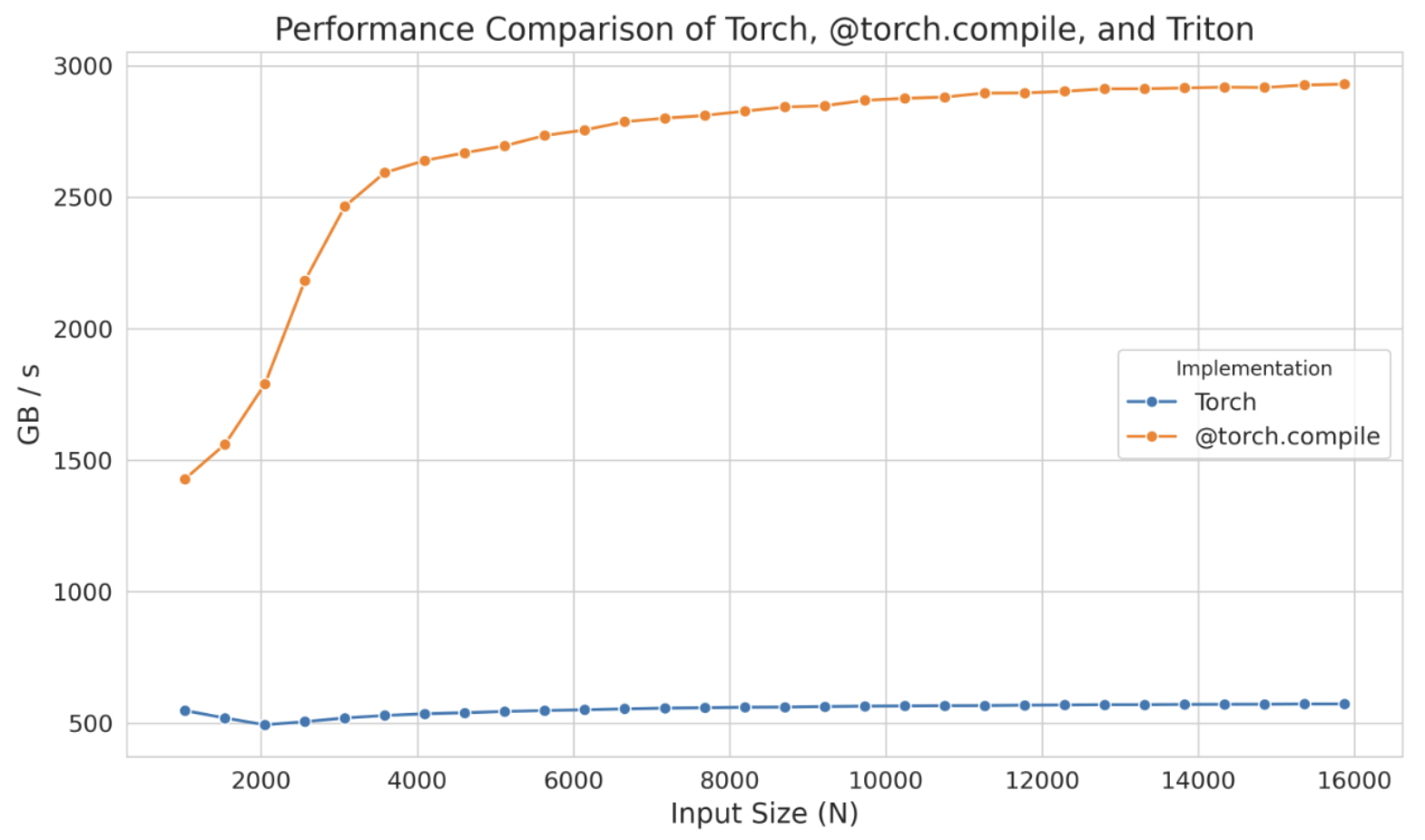
然而，如果这种性能提升不足，你可以考虑实现 Triton 内核。作为一个起点，你可以查看由@torch.compile 生成的 triton 内核。为此，你只需设置环境变量 TORCH_LOGS 为 "output_code" ：

1
export TORCH_LOGS="output_code"

一旦运行带有 @torch.compile 装饰器的 Python 脚本，它将生成并输出相应的 Triton 内核，在这种情况下，是：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
@triton.jit
def triton_(in_ptr0, out_ptr0, xnumel, XBLOCK : tl.constexpr):
    xnumel = 100000000
    xoffset = tl.program_id(0) * XBLOCK
    xindex = xoffset + tl.arange(0, XBLOCK)[:]
    xmask = xindex < xnumel
    x0 = xindex
    tmp0 = tl.load(in_ptr0 + (x0), xmask)
    tmp1 = 0.0
    tmp2 = tmp0 < tmp1
    tmp3 = tl_math.exp(tmp0)
    tmp4 = 1.0
    tmp5 = tmp3 - tmp4
    tmp6 = tl.where(tmp2, tmp5, tmp0)
    tl.store(out_ptr0 + (x0), tmp6, xmask)

为了提高可读性，我们可以修改变量名，添加注释，并进行轻微调整（或者请求LLM为我们完成），如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
@triton.jit
def elu_kernel(input_ptr, output_ptr, num_elements, BLOCK_SIZE: tl.constexpr):
    # Calculate the starting index for this block
    block_start = tl.program_id(0) * BLOCK_SIZE
    # Create an array of indices for this block
    block_indices = block_start + tl.arange(0, BLOCK_SIZE)[:]
    # Create a mask to ensure only valid indices are processed
    valid_mask = block_indices < num_elements
    # Load input values from the input pointer based on valid indices
    input_values = tl.load(input_ptr + block_indices, valid_mask)
    # Define the ELU parameters
    zero_value = 0.0  # Threshold for ELU activation
    negative_mask = input_values < zero_value
    exp_values = tl.math.exp(input_values)
    # Define the ELU output shift
    one_value = 1.0
    shifted_exp_values = exp_values - one_value

    output_values = tl.where(negative_mask, shifted_exp_values, input_values)

    # Store the computed output values back to the output pointer
    tl.store(output_ptr + block_indices, output_values, valid_mask)

此处， tl.program_id(0) 提供一个唯一的 Block ID，我们用它来确定该块将处理哪个数据部分。使用此 Block ID， block_start 计算每个块的起始索引，而 block_indices 指定该部分内的索引范围。 valid_mask 确保仅处理 num_elements 内的索引，安全地使用 tl.load 加载数据。然后应用 ELU 函数，根据数值是否为负修改值，并将结果使用 tl.store 写回内存。

当使用 triton.testing.Benchmark 对生成的内核进行基准测试时，其性能如下：

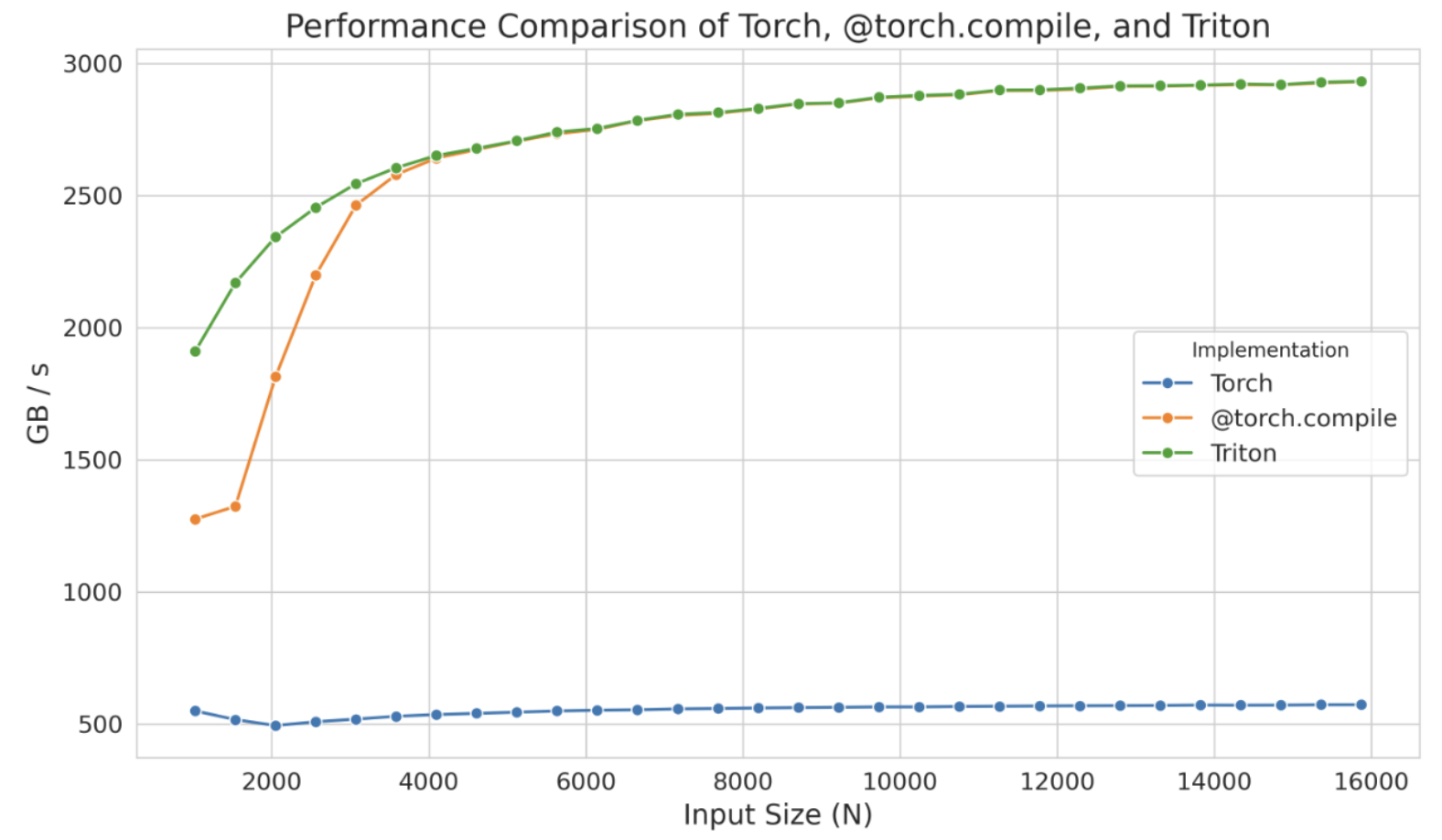
这个独立的内核在较小规模下甚至表现出比 @torch.compile 更优的性能，但这可能仅仅是 torch.compile 的编译时间影响所致。无论如何，与其从零开始，不如从这些生成的内核出发，并将精力集中在优化其性能上，从而节省大量时间。

即使在 Triton 中，有时也无法完全达到设备的峰值性能，因为该语言在处理共享内存和流多处理器（SMs）内的调度等低级细节方面存在限制。Triton 的能力仅限于块及其在 SMs 之间的调度。为了获得更深入的控制，你需要直接在 CUDA 中实现内核，在那里你将能够访问所有底层低级细节。

CUDA 方面，可以采用各种技术来提高内核的效率。这里仅介绍其中几个：优化内存访问模式以降低延迟、使用共享内存存储频繁访问的数据以及管理线程工作负载以最小化空闲时间。

在深入 CUDA 示例之前，总结一下看到的工具，这些工具使我们能够编写内核代码以在 GPU 上执行指令：

  1. PyTorch：简单但速度较慢
  2. torch.compile：简单且速度快，但灵活性不足
  3. Triton：更难，但更快、更灵活
  4. CUDA：最难，但最快、最灵活（如果掌握得当）

下面讨论 CUDA 中最常见的优化技术之一：优化内存访问。GPU 的全局内存（在前面的图表中是最大的内存）相比缓存来说，延迟较高，带宽较低，这通常是大多数应用程序的主要瓶颈。高效地访问全局内存的数据可以极大地提高性能。

内存合并

为了有效利用全局内存的带宽，理解其架构至关重要。在CUDA设备中，全局内存是使用DRAM实现的。

内存归约（Memory coalescing）利用 DRAM 在访问内存地址时以突发或连续内存位置范围的形式提供数据的特点。每次访问 DRAM 位置时，包括请求的位置在内的连续位置序列由 DRAM 芯片中的多个传感器并行读取。一旦读取，这些数据可以快速传输到处理器。在 CUDA 中，归约 coalescing 利用这种突发行为，通过确保 warp 中的线程（32 个执行相同指令的线程，SIMD）访问连续的内存位置，以最大化内存访问效率。

例如，如果线程 0 访问位置 M，线程 1 访问 M + 1，线程 2 访问 M + 2，依此类推，GPU 硬件将这些请求归约或合并为一个大型、高效的 DRAM 突发访问请求，而不是单独处理每个访问。

以矩阵乘法为例。一个简单直接的实现方式是，每个线程计算输出矩阵的一个元素，如下：

1
2
3
4
5
6
7
8
9
10
11
12
13

__global__ void matmul_naive(int M, int N, int K, const float *A, const float *B, float *C) {
    const uint x = blockIdx.x * blockDim.x + threadIdx.x;
    const uint y = blockIdx.y * blockDim.y + threadIdx.y;

    if (x < M && y < N) {
        float tmp = 0.0;
        for (int i = 0; i < K; ++i) {
            tmp += A[x * K + i] * B[i * N + y];
        }
        C[x * N + y] = tmp;
    }
}

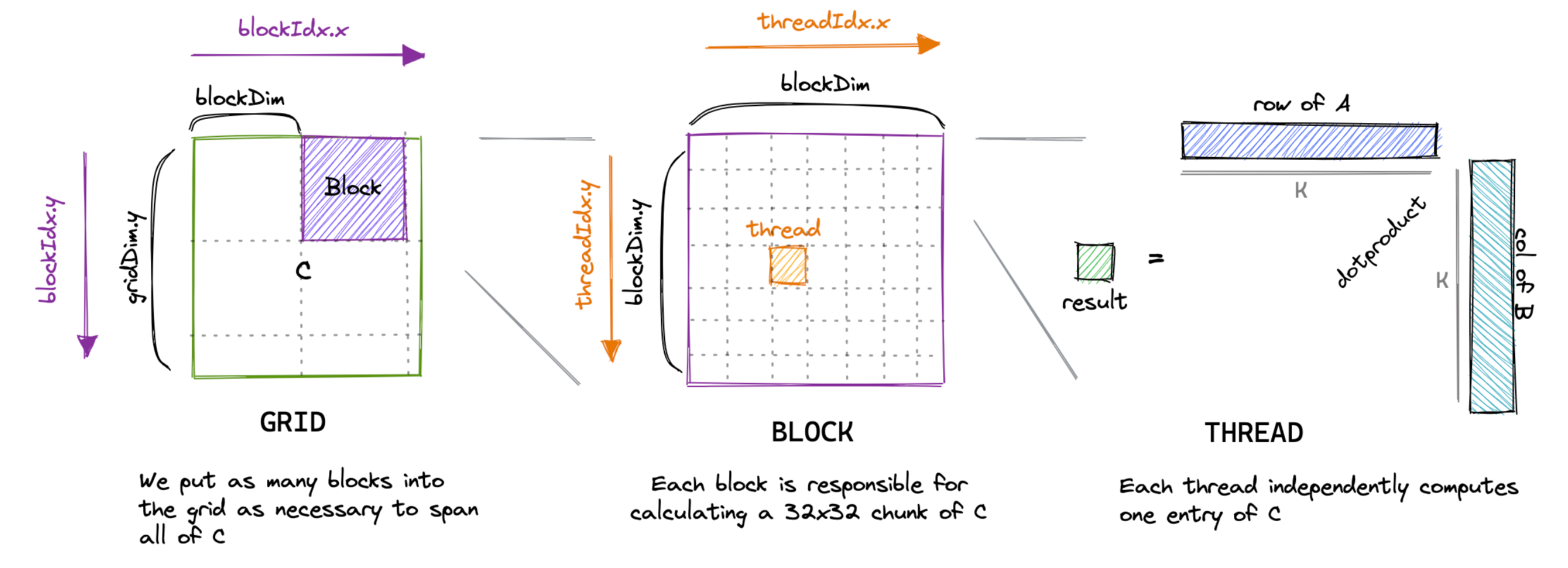
这是一篇精彩博客文章[2]中内核的优秀可视化：

然而，当使用类似 ncu 的工具对内核进行性能分析时，可以看到问题，包括低内存吞吐量和未归约的内存访问。

原因在于，在此内核中，同一块中的两个线程（线程 ID 为 (0, 0) 和 (1, 0)，最终将位于同一 warp 中）将同时从矩阵 B 的同一列加载，但矩阵 A 的不同行。由于矩阵元素按行主序存储（意味着行元素位于连续的内存地址中，如图所示），线程 (0, 0) 将在第一次迭代 $i = 0$ 中加载 $A_{0,0}$ ，而线程 (1, 0) 将加载 $A_{1,0}$ 。这些元素在内存中并不相邻，这种错位将在每次迭代中存在，从而防止内存访问归约。

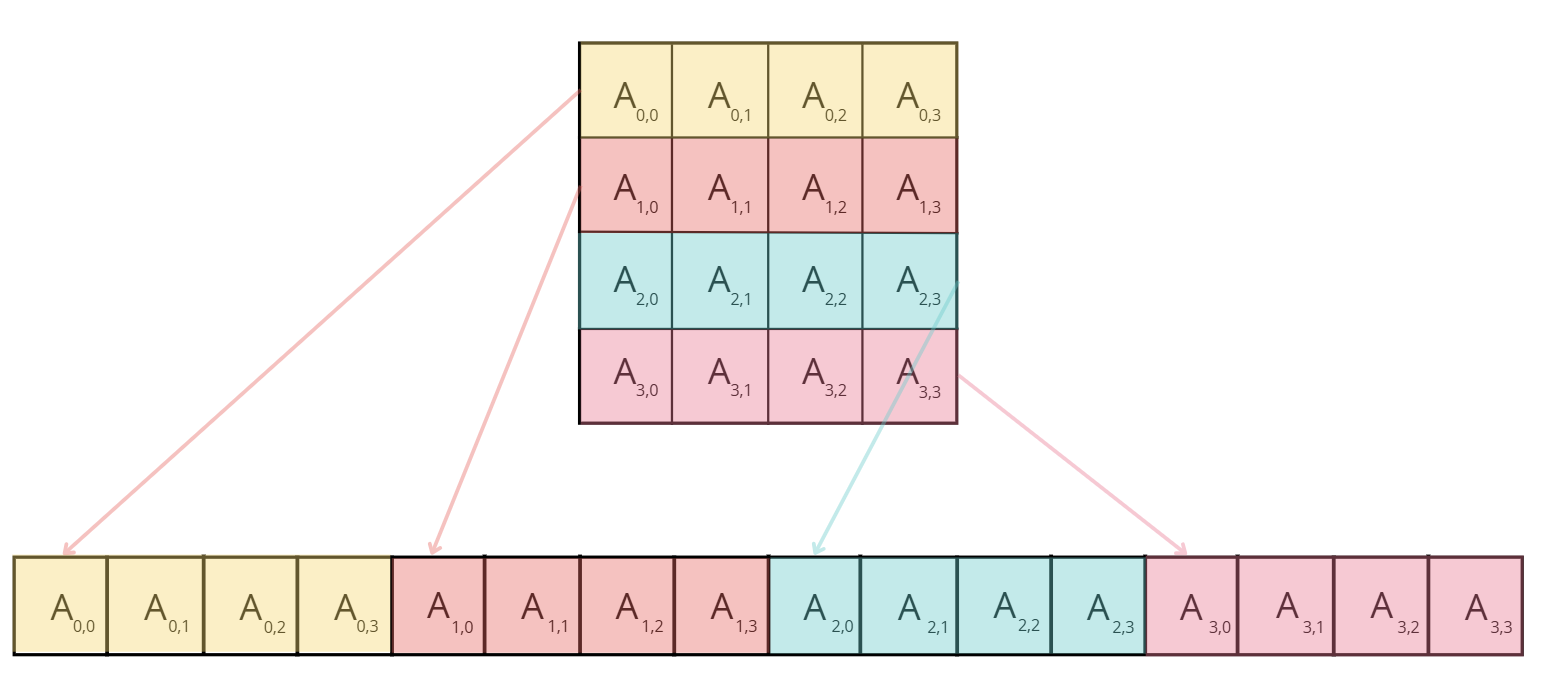
为了提高我们内核的性能，我们可以改变坐标 x 和 y 的计算方式，如下所示：

1
2
3
4
5
6
7
8
9
10
11

const int x = blockIdx.x * BLOCKSIZE + (threadIdx.x / BLOCKSIZE);
const int y = blockIdx.y * BLOCKSIZE + (threadIdx.x % BLOCKSIZE);

if (x < M && y < N) {
 float tmp = 0.0;
 for (int i = 0; i < K; ++i) {
     tmp += A[x * K + i] * B[i * N + y];
  }
  C[x * N + y] = tmp;
}

而不是使用二维块，我们切换到一维块，并重新定义确定 x 和 y 值的方法。在这种新方法中，同一 warp（具有接近的 threadIdx.x 值）内的线程将共享相同的 x 值，但具有不同的 y 值。这意味着它们将加载矩阵 A 的同一行，但矩阵 B 的不同列。因此，可以合并行主序矩阵的内存访问。

当我们对新的内核进行性能分析时，注意到关于未归约内存访问的警告已经消失，GPU 的内存吞吐量大约提高了 10 倍。

内核的执行时间降低了 10 倍！惊人。

现在让我们介绍另一种在文献中经常提到的技术：分块Tiling。

分块处理（Tiling）

分块处理是一种利用 共享内存 Shared Memory 优化内存访问模式的技术。正如我们前面提到的，共享内存是一种小而快速的存储，块内的所有线程都可以访问它。这使得数据可以被多个线程重复使用，从而减少了从较慢的全局内存中重复加载数据的需求。

以矩阵乘法为例，块中的每个线程可能需要从两个矩阵（如 A 和 B）中获取元素。如果每个线程独立地从全局内存加载所需的行和列，就会出现大量冗余加载，因为块中的多个线程会访问重叠的数据。相反，我们可以使用分块处理 Tiling，将 A 和 B 的一个块（或 Tile）一次性加载到共享内存中，让该块中的所有线程重复使用相同的共享数据。

在分块处理的方法中，每次迭代时，块内的所有线程协同工作，将两个 Tile（一个来自矩阵 A，另一个来自矩阵 B）加载到共享内存中。具体来说，线程加载矩阵 A 的一个Tile（大小为 BLOCK_SIZE_M × BLOCK_SIZE_K）以及矩阵 B 的一个Tile（大小为 BLOCK_SIZE_K × BLOCK_SIZE_N）。一旦这些Tile存入共享内存，线程就可以在这些Tile上执行矩阵乘法，从而实现高效计算，因为所有必要的数据都可以被快速访问。Tile乘法的结果存储在一个累积矩阵中，该矩阵保存中间结果。在每次迭代后，当前Tile乘法的结果都会累加到该矩阵中，直到两个矩阵的所有Tile都被处理完毕。

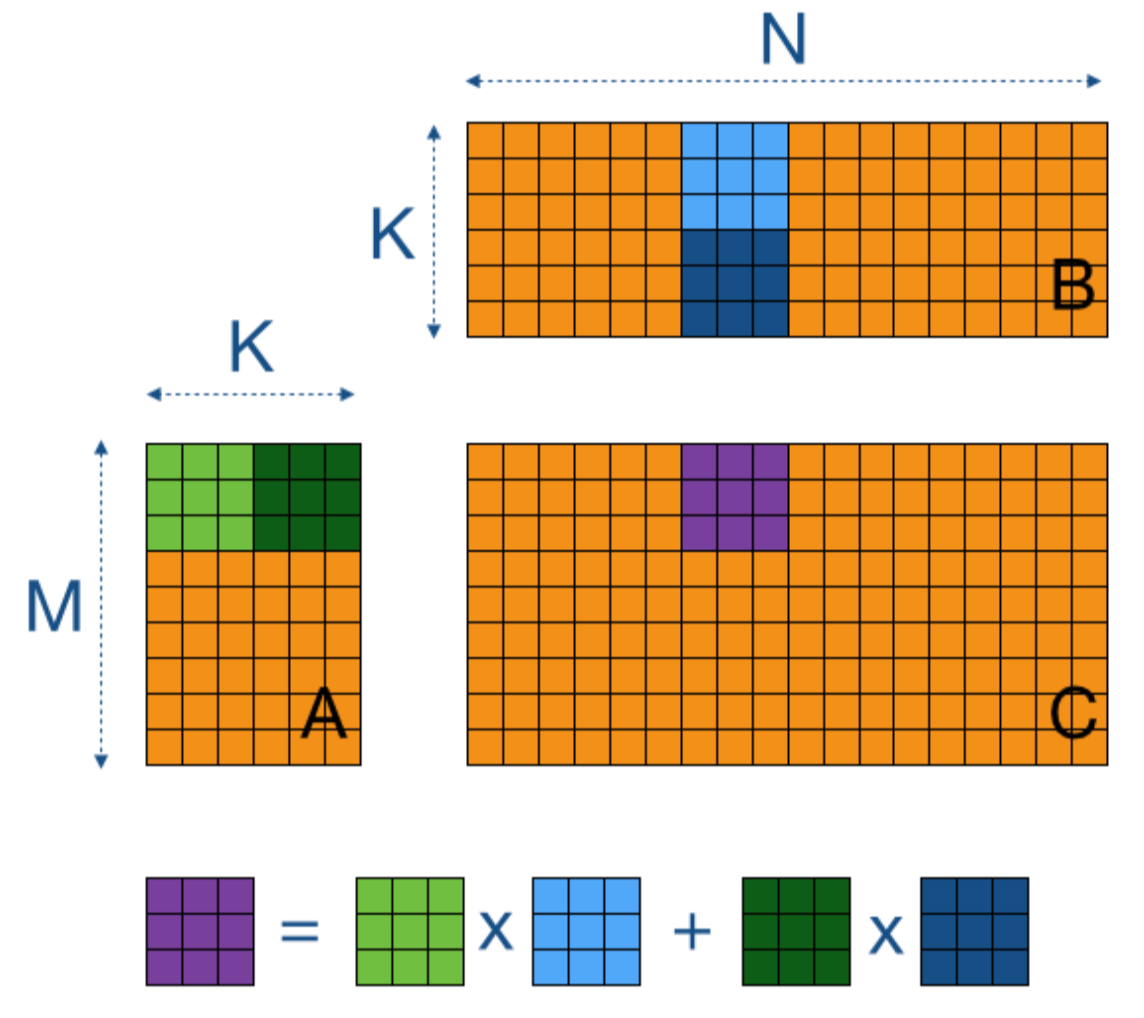
让我们来看看实现中的关键部分：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

// Set pointers to the starting elements
A += blockRow * TILE_SIZE * K; // Start at row = blockRow, column = 0
B += blockCol * TILE_SIZE; // Start at row = 0, column = blockCol
C += blockRow * TILE_SIZE * N + blockCol * TILE_SIZE; // Start at row = blockRow, column = blockCol
float sum = 0.0;
// The outer loop moves through tiles of A (across columns) and B (down rows)
for (int tileIdx = 0; tileIdx < K; tileIdx += TILE_SIZE) {
sharedA[localRow * TILE_SIZE + localCol] = A[localRow * K + localCol];
sharedB[localRow * TILE_SIZE + localCol] = B[localRow * N + localCol];

// Ensure all threads in the block have completed data loading
__syncthreads();

// Shift pointers to the next tile
A += TILE_SIZE;
B += TILE_SIZE * N;

// Compute the partial dot product for this tile
for (int i = 0; i < TILE_SIZE; ++i) {
    sum += sharedA[localRow * TILE_SIZE + i] * sharedB[i * TILE_SIZE + localCol];
}
// Synchronize again to prevent any thread from loading new data
// into shared memory before others have completed their calculations
__syncthreads();
}
C[localRow * N + localCol] = sum;

每个线程首先从矩阵 A和矩阵 B中加载一个元素到共享内存。在这种情况下，实现合并内存访问（coalesced memory access）非常直观：通过将 threadIdx.x 作为局部列索引（localCol），同一个 warp 中的线程可以访问相邻的矩阵元素。块内所有线程完成数据加载后（通过调用 __syncthreads() 确保同步），它们就会计算这两个Tile的点积。当所有Tile遍历完成——矩阵 A 在水平方向移动，矩阵 B 在垂直方向移动——最终计算出的结果存入矩阵 C的对应位置。

当我们使用 ncu 对这个内核进行基准测试时，我们发现内存吞吐量增加到了 410 Gb/s，内核执行时间减少了约 43%，实现了约 6.6 TFLOPs 的性能。

线程粗化（Thread Coarsening）

分块处理技术显著提高了我们内核的性能。但是，当分析量化每个状态中花费的周期的warp状态时，我们观察到以下情况：

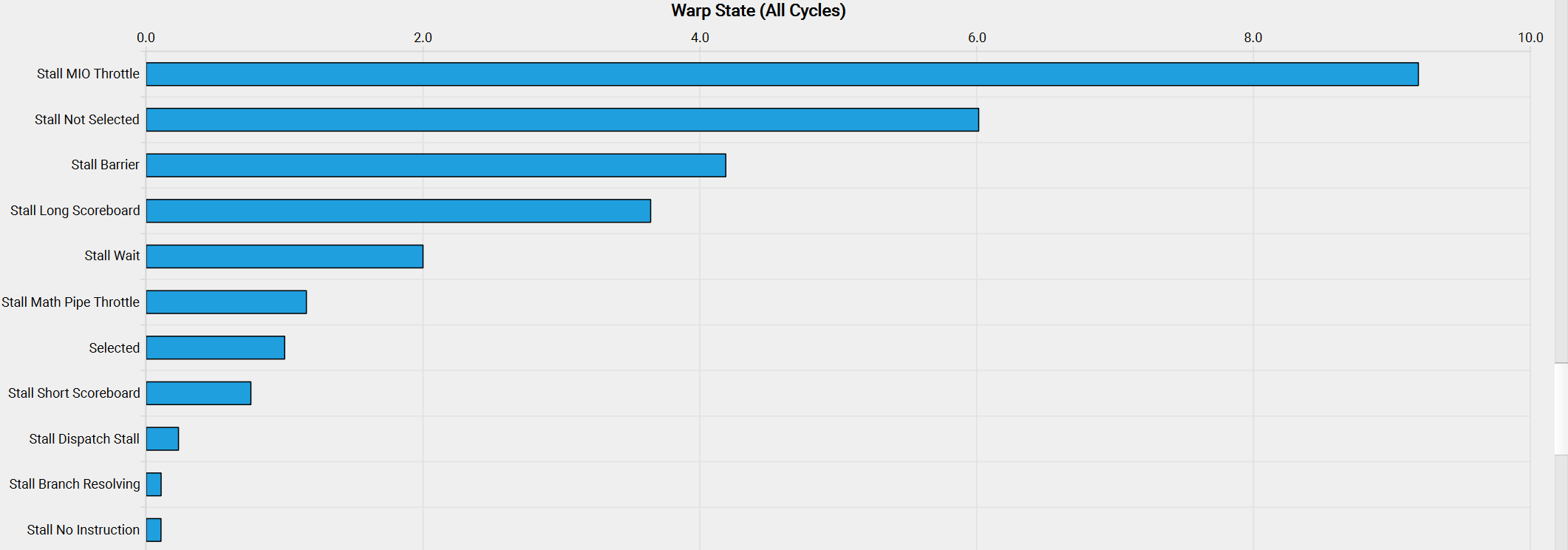
这些神秘状态名称的含义可以在[NVidia的性能指南]https://docs.nvidia.com/nsight-compute/ProfilingGuide/index.html#metrics-reference中找到，在Warp Stall Reasons部分可以阅读到：

*"smsp__pcsamp_warps_issue_stalled_mio_throttle: 等待MIO（内存输入/输出）指令队列不再满的Warp被停顿。在MIO管道（包括特殊数学指令、动态分支以及共享内存指令）极端利用的情况下，此停顿原因较高。当由共享内存访问引起时，尝试使用更少但更宽的加载可以减少管道压力。*

所以看起来Warp正在等待共享内存访问返回！为了解决这个问题，我们可以应用一种称为 线程粗化 Thread Coarsening 的技术，该技术涉及将多个线程合并为一个粗化线程。这将显著减少共享内存访问，因为每个粗化线程可以处理多个输出元素。

在写入或改进自定义内核时，一个最重要的考虑因素：最小化控制分歧 Minimizing Control Divergence。

最小化控制分歧

流多处理器（SM）被设计为使用单指令多数据（SIMD）模型执行 warp 中的所有线程。这意味着在任何给定时刻，一个指令同时为warp中的所有线程获取和执行。当执行warp时，其中的线程在数据的不同段上操作，但遵循相同的指令，因此得名单指令多数据。SIMD的主要优势在于其效率；负责指令获取和调度的控制硬件在多个执行单元之间共享。这种设计最小化了与控制功能相关的硬件开销，使得更大比例的硬件专注于提高算术吞吐量。

当warp内的线程采取不同的执行路径时，就会发生控制分歧。例如，如果条件语句（如 if语句）导致一些线程执行一个代码块，而其他线程执行另一个代码块，那么warp必须串行执行这些执行，导致空闲线程等待其他线程完成。为了最小化控制分歧，我们需要设计内核，**确保warp内的线程遵循相同的执行路径。这可以通过重构代码以减少分支、**使用确保所有线程遵循类似执行路径的数据结构，或使用预测等技术来实现。

编者注：简单理解为不要有if等判断语句

我们已经介绍了写入自定义内核和改进GPU操作性能和内存占用的一些主要考虑因素。但在转向实际示例之前，还有一个重要的概念需要讨论：“融合内核 Fused Kernel”。

融合内核（Fused Kernels）

之前提到GPU和CPU操作可以异步进行。特别是，CPU上的 Host Code 主机代码可以以非阻塞方式调度GPU的工作负载。

非阻塞对于重叠通信和计算非常有用——可以扩展到更一般的想法，即尽量避免来回在主机和GPU内核命令之间切换。

这个想法在 Horace He [4] 的这些图中得到了很好的诠释：

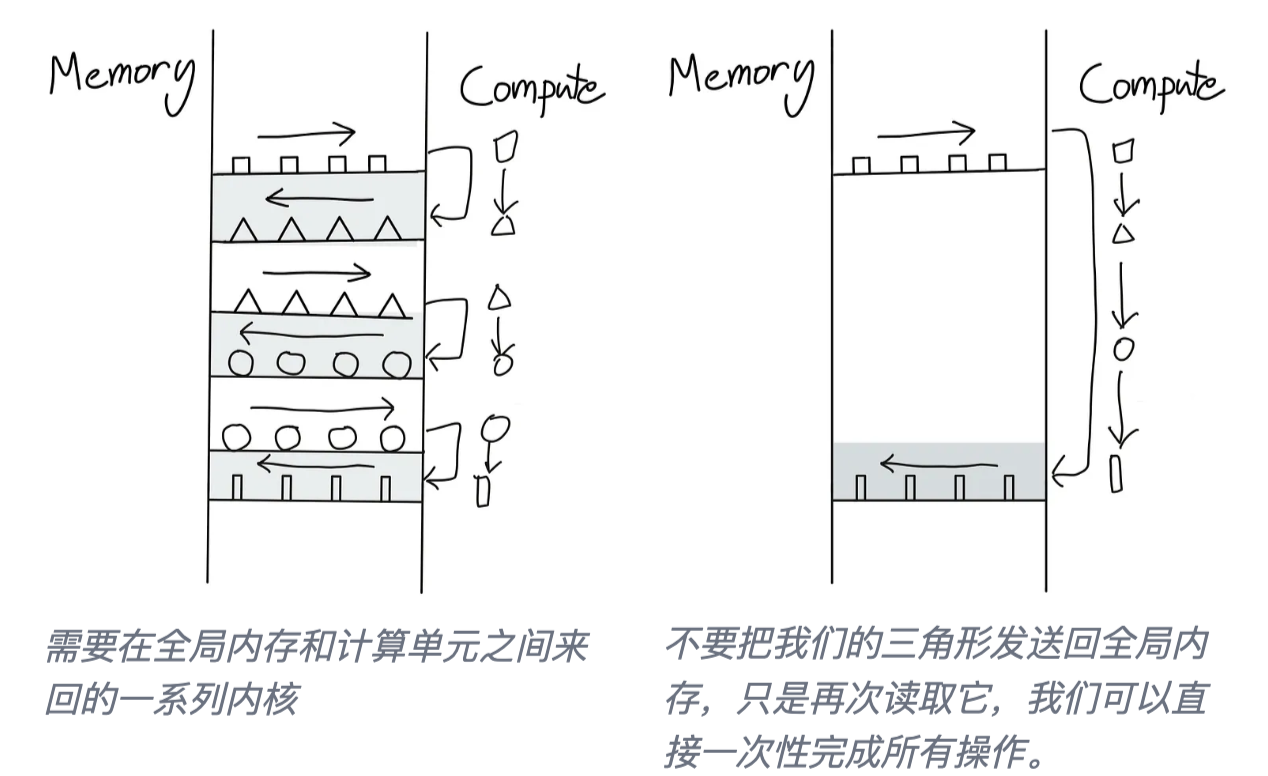
如何避免这种来回？最好的办法是尽可能让我们的 GPU 实现自主。这通过将尽可能多的连续计算操作打包在一个单独的内核中来实现，这个内核被称为“融合内核 Fused Kernel”。

融合内核对于独立于彼此在各个输入Tokens上执行的一系列点状操作特别高效且易于编写。在这种情况下，在将计算值移动到 SM 内存并启动新内核之前，没有必要将计算值返回到全局内存。在完成计算序列之前，将所有值保留在本地要高效得多。

Transformer 模型中有许多地方可以应用这种“融合”方法：每次我们遇到一系列逐点point-wise操作，例如在层归一化计算中。

现在我们已经掌握了欣赏内核工程的真正杰作所必需的所有理解：Flash Attention

Flash Attention 1-3

Flash attention是由Tri Dao [5] 引入，并提出通过编写自定义CUDA内核来优化注意力计算，使其更快且更内存高效。Flash Attention的核心思想是充分利用GPU的各种内存，避免过度依赖最慢的内存之一：GPU的全局内存。

编者注： 在Flash attention中，HBM - 高带宽内存 High band Memory 就是GPU全局内存。

注意机制的基本实现涉及在内存和worker之间进行大量传输。它要求在HBM中实现S和P矩阵，这意味着结果需要发送到HBM，然后再次发送到SRAM进行下一步计算：

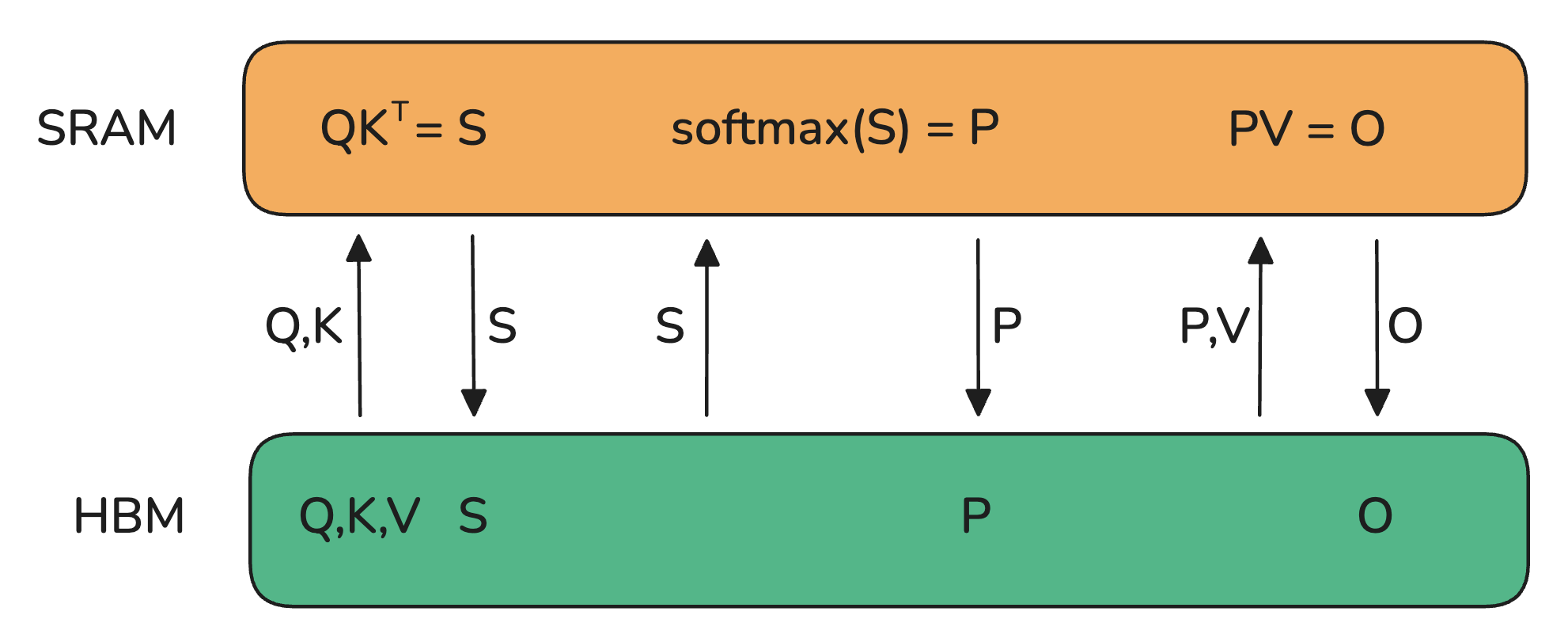
由于HBM的带宽较低，这在注意力计算中引入了严重的瓶颈。关键元素是将S矩阵计算成可以适应SM较小共享内存的小块。但可以做得更好，不仅仅是分块计算S矩阵，而是完全避免存储庞大的S矩阵，仅保留计算Softmax归一化因子所需的统计信息。这样，可以直接在SRAM中一次性计算部分 O，而无需在中间结果之间来回传输数据。这不仅利用了共享内存，还消除了由于存储注意力矩阵（在长上下文长度下是模型中最大的激活矩阵之一）而导致的内存瓶颈。

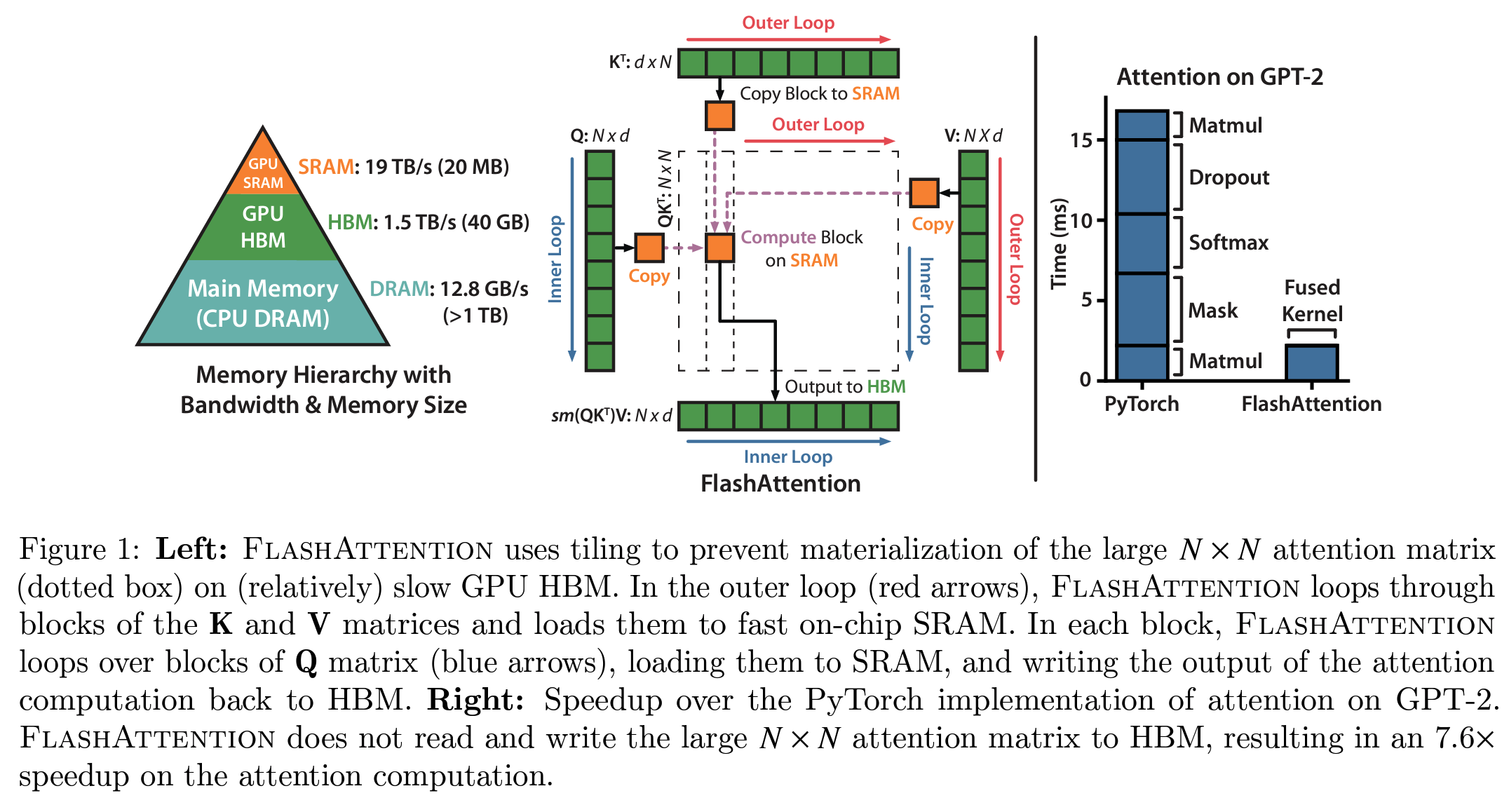
Flash Attention 的理念解决了模型训练中的众多瓶颈，因此迅速成为所有Transformer模型执行注意力计算的默认方法：

  • 通过避免存储S矩阵，降低了注意力计算的内存负担
  • 消除了大部分注意力计算的平方复杂度(S²)所带来的影响

因此，自Transformer架构发明后不久发展出的所有线性注意力变体和次二次近似注意力方法大多被搁置，取而代之的是这种精准且快速的Flash Attention实现和机制。

在Flash Attention 1发布之后，同一实验室相继推出了两个改进版本：Flash Attention 2 和 3。与Flash Attention 1相比，Flash Attention 2 和 3 的改进更多体现在对GPU的底层优化，而不是对注意力机制本身的改动。具体来说：

  • 减少非矩阵乘法（matmul）操作的数量
  • 精细划分计算任务至warp和线程块（适用于Flash Attention 2）
  • 在最新的Hopper架构（H100）上优化FP8和Tensor Core的支持（适用于Flash Attention 3）

Flash Attention 是一个典型案例，展示了当深入考虑当前GPU加速器的内存/计算设计时，所能带来的突破性改进。

到目前为止，我们讨论的算子融合技术要求对模型代码进行改动，并为特定操作编写自定义内核，以加速训练。

在计算操作的底层优化的最后部分，我们将探索一系列与模型代码无关的方法，这些方法适用于任何模型，并且已经成为业界标准：混合精度训练（Mixed Precision Training）！

混合精度训练（Mixed Precision Training）

在本书的多个章节中，我们讨论了低精度数值格式及其对存储激活值、参数和优化器状态的内存需求的影响。现在，我们将深入了解这些格式的细节，并更好地理解它们的权衡、优势和局限性。

顾名思义，混合精度训练涉及在训练过程中混合使用不同的数值精度。PyTorch张量的默认数值精度是单精度浮点格式，即FP32（float32），这意味着每个存储的数值占用32位（4字节）。这些位被分为三个部分：

  • 符号位（Sign）：第一个比特决定数值是正数还是负数
  • 尾数（Mantissa）：决定数值的有效数字
  • 指数（Exponent）：控制数值的数量级

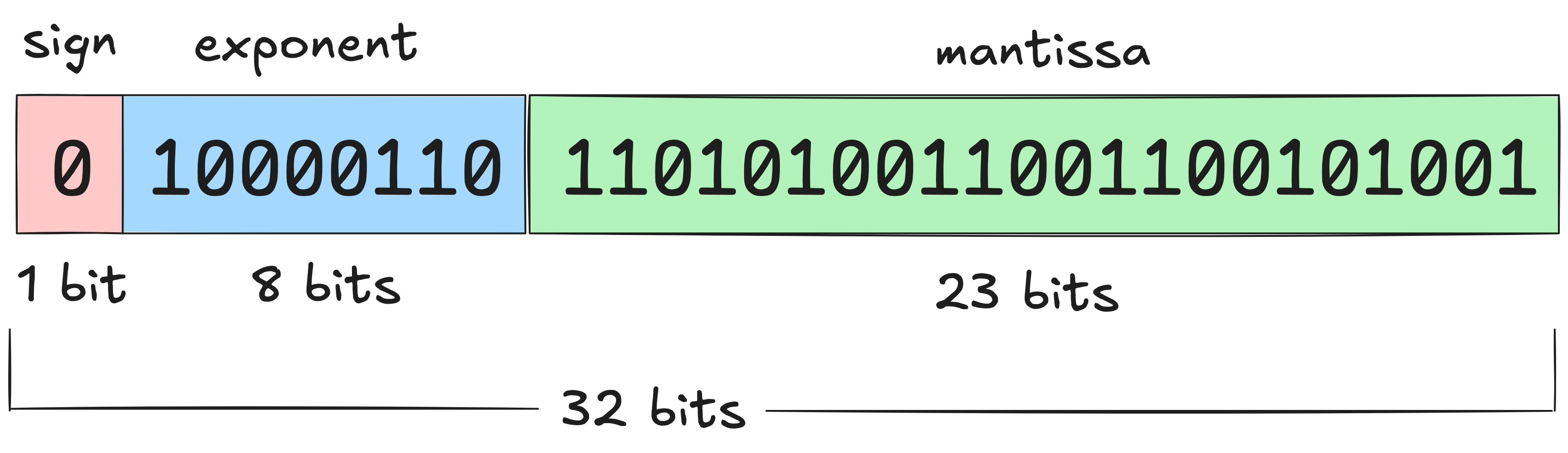
浮点数的基本原理可以通过科学计数法轻松理解，例如−5.734× $10^7$，其中首先是符号位，然后是尾数和指数。这样可以在广泛的数值范围内以自适应精度表示数值。虽然float32是默认格式，但PyTorch还支持多种浮点格式：

格式 总位数 符号位 指数位 尾数位
float32 32 1 8 23
float16 16 1 5 10
bfloat16 16 1 8 7
float8 (e4m3) 8 1 4 3
float8 (e5m2) 8 1 5 2

减少总位数并非没有代价（这里也没有免费午餐），但可以控制如何付出代价。我们可以在尾数或指数上牺牲更多位数。因此，也存在两种float8格式，根据指数和尾数命名，灵活选择最合适的格式。我们可以查看每种格式的可能数值范围：

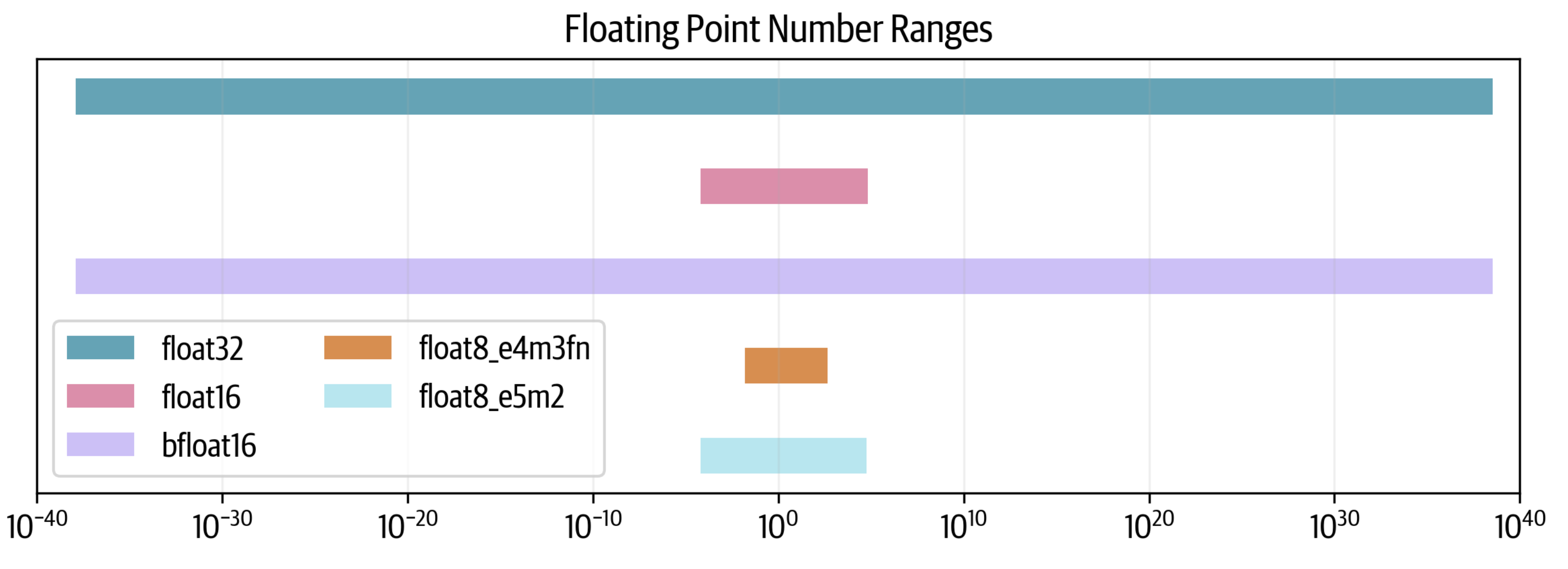
我们可以看到，float32跨越80个数量级，而float16牺牲了很多范围，而bfloat16保持了完整的范围。两种float8格式进一步减少了范围，其中e5e2可以维持float16的范围，而e4m3的范围更小。

为什么有些格式能够保持范围，而其他格式则不能？让我们通过在 1 和 2 之间绘制 10,000 个点来查看分辨率 resolution。每个点将根据每种格式四舍五入到最接近的可表示数字。

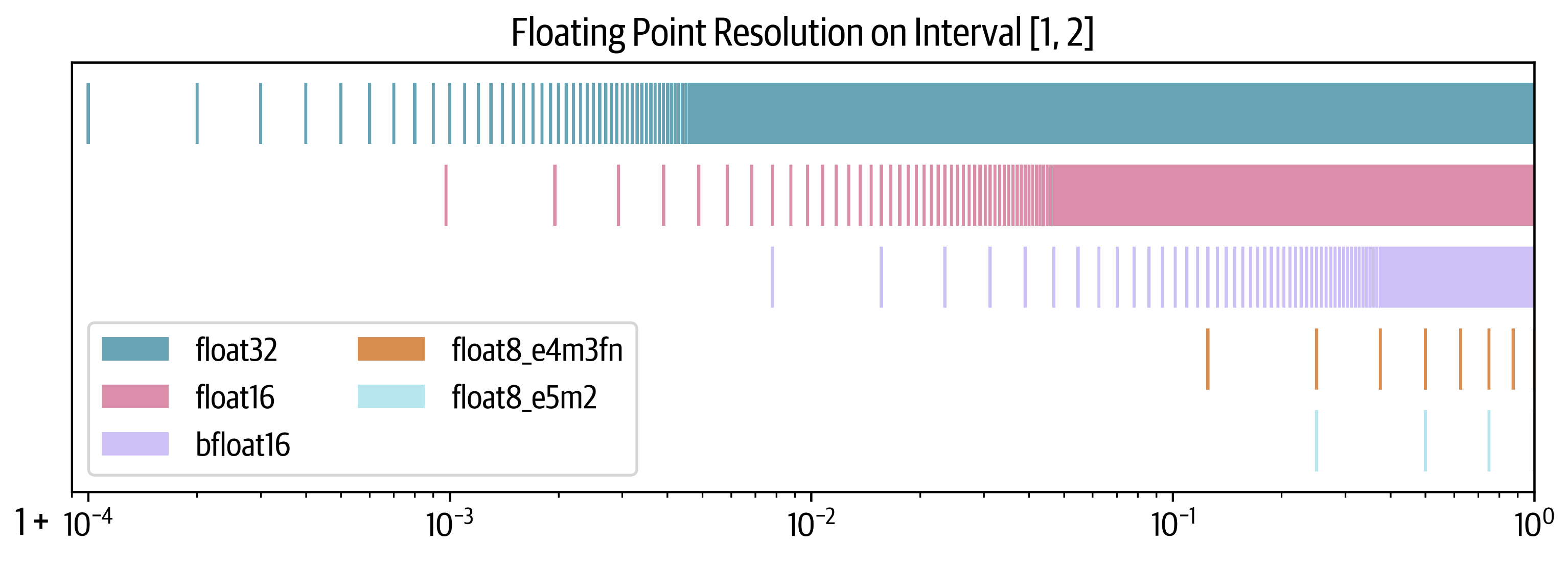
我们可以看到，bfloat16通过牺牲更多精度来维持float32的范围，但这是有代价的。在float8的情况下，情况更为严峻，因为e4m3在区间1-2内只能表示7个数字，而e5m2只能表示3个数字。

衡量格式分辨率的常见指标是epsilon：即1.00后的第一个可表示的数字。可以看到，对于float32格式， $10^{−4}$ 是一个上界（实际上是 $1.19^{−7}$）。对于float16，它是 $10^{−3}$，而对于bfloat16，则是其10倍。

混合精度训练的理念是使用其中一些较低精度格式，同时保持全精度训练的性能。

事实证明，我们不能完全放弃float32，并且通常需要保持一些部分以全精度进行训练。这就是为什么较低精度训练通常被称为混合精度训练。

现在来看看使用16位进行模型训练，然后看看能否进一步降至8位。

FP16和BF16训练

简单地将所有张量和操作切换到float16通常不起作用，结果通常是发散的损失。然而，原始的混合精度训练论文 [6] 提出了三种技巧来匹配float32训练：

  1. FP32权重复制：float16权重可能会出现两个问题。在训练期间，某些权重可能变得非常小，并且会被舍入为0。但即使权重本身不接近零，如果更新非常小，其数量级的差异可能会导致在加法过程中权重下溢。一旦权重为零，它们将在训练的其余过程中保持为零，因为再也没有梯度信号传递过来了。
  2. 损失缩放：梯度也存在类似的问题，因为梯度往往远小于1，因此有可能下溢。一个简单而有效的策略是在反向传播之前对损失进行缩放，在反向传播之后取消缩放梯度。这确保在反向传播过程中没有下溢，并且在进一步处理梯度（例如剪裁）和优化步骤之前取消缩放，不影响训练。
  3. 累积：最后，在16位精度下执行某些算术运算（如平均值或求和）时，也可能面临下溢或上溢的问题。一种解决方案是在操作过程中累积中间结果到float32，并仅在最后将最终结果转换回16位精度。

通过这些技术，可以实现稳定的训练，同时由于更快的低精度算术运算，获得更高的吞吐量。当然，你可能会问：我们是否可以比16位精度更进一步、更快？也许可以！

FP8预训练

即使完全重叠了通信与计算，我们总会遇到硬件本身的底层理论FLOPS限制，即硬件上每个操作的效率。这就是数值精度变得至关重要的地方。例如，在NVIDIA的H100 GPU上，FP8矩阵乘法（GEMM操作）的效率达到bfloat16的两倍，使得低精度训练进一步有吸引力。最近的研究，包括FP8-LM [7], torchao [8]，以及DeepSeek-V3 [9]，展示了FP8训练在大规模模型中的潜力。然而，FP8预训练引入了一个重大挑战：稳定性。在低精度下，数值不稳定往往导致损失发散，难以达到高精度训练的准确性。

我们知道，对于固定模型大小，随着学习率的提高，不稳定性会增加[10]，使得FP8预训练尤为棘手。以下是FP8训练通常发散损失曲线的示例：

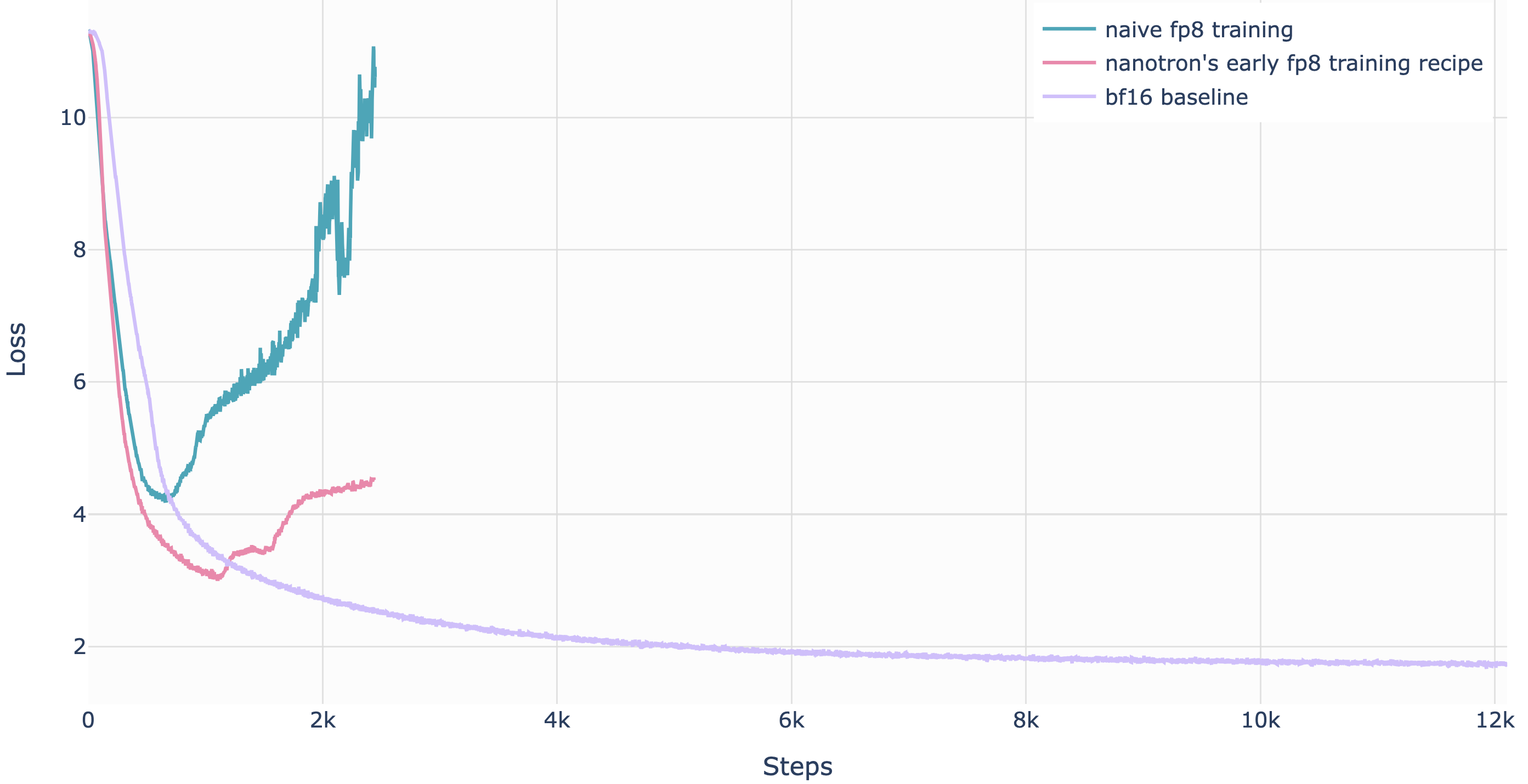
首次成功的大规模FP8混合精度训练在DeepSeek-V3上被公开报道。研究人员仔细分析了前向传播（Fprop）以及激活（Dgrad）和权重（Wgrad）反向传播的每个操作。类似于BF16混合精度训练，一些聚合计算和主权重仍然保持高精度，而实际的运算则在FP8中执行。

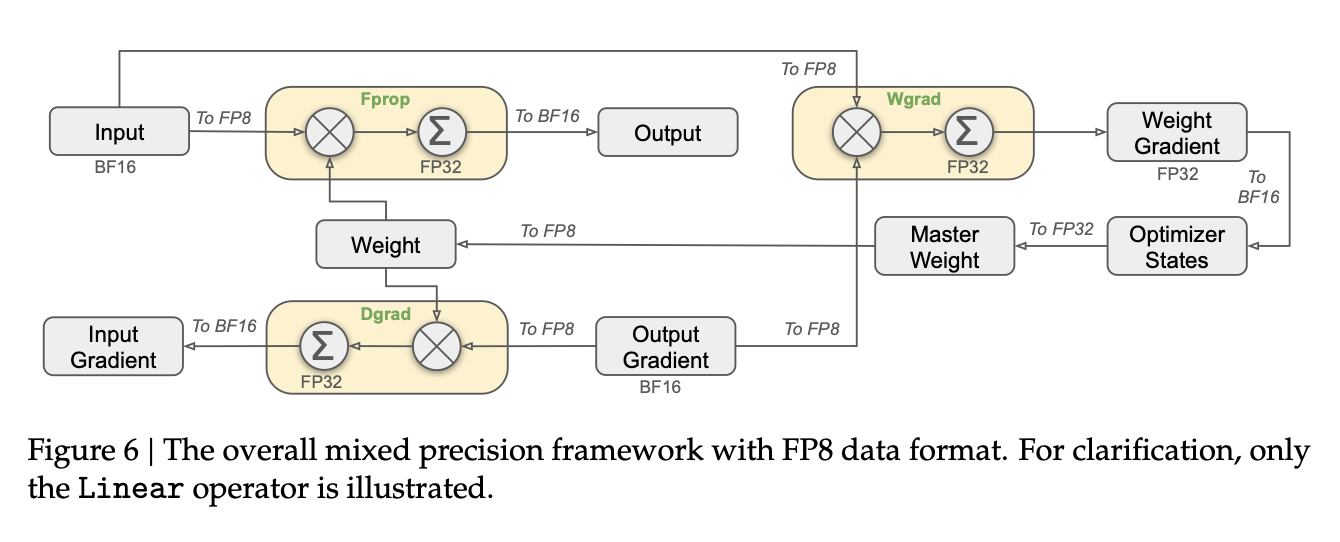
为了从高精度（如FP32或BF16）切换到更低精度（如FP16或FP8）并适应更小的数值范围，需要对激活值的范围进行归一化，例如计算其绝对最大值。DeepSeek-V3进一步引入了一种特定的量化方案，其中范围按块（tile）归一化：输入/激活使用1×128，权重和缩放因子使用128×128。这种方法使归一化过程不易受到激活值中异常值的影响。此外，他们还提出了一些额外的技巧，以进一步减少内存和通信开销，具体内容可以在DeepSeek-V3技术报告的第3.3节中找到。以下是一些已知的FP8训练方法的总结：

GEMM计算精度 主模型权重 累积梯度 模型权重 梯度 优化器状态 总内存占用
bfloat16 + fp32混合精度基线 bf16 fp32 fp32 bf16 bf16 fp32 + fp32 4 + 4 + 2 + 2 + 4 + 4 = 20字节
去除FP32梯度累积 bf16 fp32 无 bf16 bf16 fp32 + fp32 4 + 2 + 2 + 4 + 4 = 16字节
Transformer Engine  Transformer 引擎 fp8 无 无 fp32 fp32 fp32 + fp32 4 + 4 + 4 + 4 = 16字节（20%减少）
FP8-LM的O3级别 fp8 fp16 fp16 fp8 fp8 fp8 + fp16 2 + 2 + 1 + 1 + 1 + 2 = 9字节（55%减少）
DeepSeek-V3 fp8 fp32 fp32 fp8 bf16 bf16 + bf16 4 + 4 + 1 + 2 + 2 + 2 = 15字节（25%减少）
nanotron的FP8  纳米通 FP8 fp8 bf16 fp32 fp8 fp8 fp8 + fp8 2 + 4 + 1 + 1 + 1 + 1 = 10字节（50%减少）

总体而言，在2025年初，FP8仍然是一种实验性技术，相关方法仍在不断发展。鉴于其明显的优势，它很可能很快成为标准，并取代bf16混合精度训练。想要了解FP8训练技术的开源实现，可以查看nanotron的实现[11]。

展望未来，下一代NVIDIA Blackwell芯片也宣布将支持FP4训练，这将进一步加速训练，但无疑也会带来新的训练稳定性挑战。

结论

恭喜你，亲爱的读者，你坚持到了最后！我们完成了一次精彩的旅程：从理解如何在单个GPU上训练简单模型，到掌握在数千个GPU上高效训练Llama-405B和DeepSeek-V3等大规模语言模型的复杂技术。现在，你应该能够相对轻松地理解Llama-3的4D并行架构图：

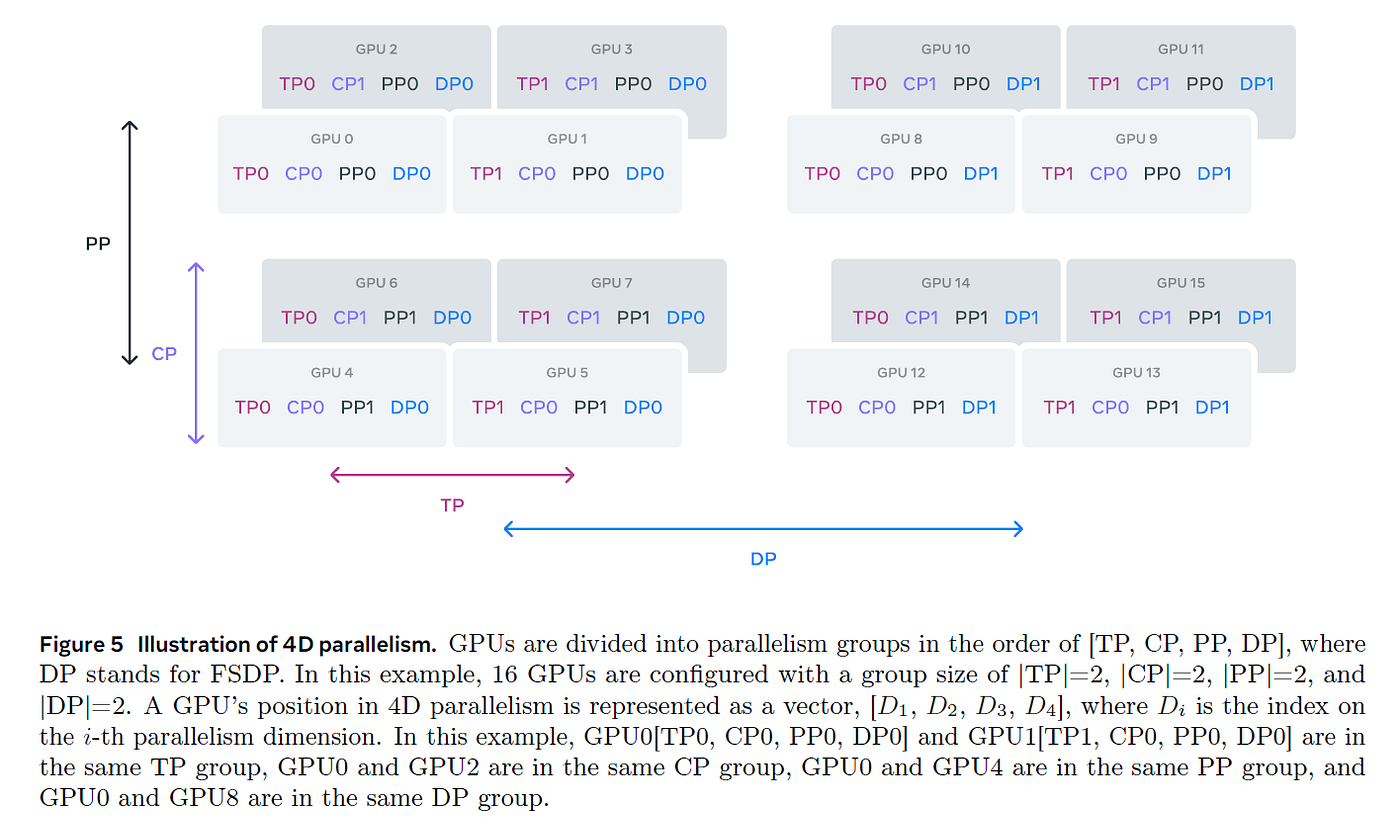
在GPU集群上高效训练大型LLM并非易事。我们学习了如何优化计算和GPU间通信，以确保它们始终处于最大化利用率。这涉及为特定模型和集群规模选择合适的并行策略，在可能的情况下重叠通信和计算，并编写自定义核函数，以充分利用硬件架构，使运算尽可能快地执行。

你可能会认为这些知识相对小众，仅适用于少数从事LLM预训练的研究人员。历史上确实如此，但随着AI开发者社区和模型规模的迅速增长，越来越多的人在推理、微调和训练中使用分布式技术，使分布式训练变得越来越普遍。因此，深入学习分布式计算正当其时。

这不仅是你的学习旅程，也是我们的学习之旅！在GPU集群上运行数千次基准测试比我们预想的更具挑战性，我们也希望与你分享我们的学习经验。

那么，接下来呢？

你现在对主要的分布式训练概念有了很好的理解，但同时，我们也只是触及了许多工具和技术的表面。以下是我们推荐的深入学习步骤：

  • 仔细阅读一些重要的或最新的论文。在参考文献部分，你可以找到许多影响深远的论文、博客文章和书籍。
  • 从零开始实现一个算法。通常，只有自己动手实现，方法才能真正“豁然开朗”。
  • 深入研究一个广泛使用的框架，并开始贡献：修复bug、回答问题或实现新功能。这是进入任何机器学习领域的最佳途径！

我们希望这本书能帮助你入门分布式训练，并希望你能训练出下一代优秀的模型！

参考文献

[1] https://resources.nvidia.com/en-us-tensor-core

[2] https://siboehm.com/articles/22/CUDA-MMM

[3] https://docs.nvidia.com/nsight-compute/ProfilingGuide/index.html#metrics-reference

[4] https://horace.io/brrr_intro.html

[5] https://tridao.me/

[6] Mixed Precision Training

[7] FP8-LM: Training FP8 Large Language Models http://arxiv.org/pdf/2310.18313.pdf

[8] torchao: PyTorch native quantization and sparsity for training and inference https://github.com/pytorch/torchao

[9] DeepSeek-V3 Technical Report

[10] Small-scale proxies for large-scale Transformer training instabilities

[11] https://github.com/huggingface/nanotron/pull/70

附录章节

并行编程速成

将LLM训练从单个GPU扩展到数百个GPU需要在所有机器之间进行权重、梯度和数据的通信与同步。有一组分布式模式可以实现这一点，称为集合操作 Collective Operation。在本节中，将进行一个小型的速成课程，涵盖诸如广播 BroadCast、全局归约 AllReduce、分发 Scatter 等操作。

现在，我们有许多独立的节点，可以是CPU核心、GPU或计算节点。每个节点执行一些计算，然后我们希望将结果或其部分传输到其他节点，用于下一个计算步骤（t+1）。

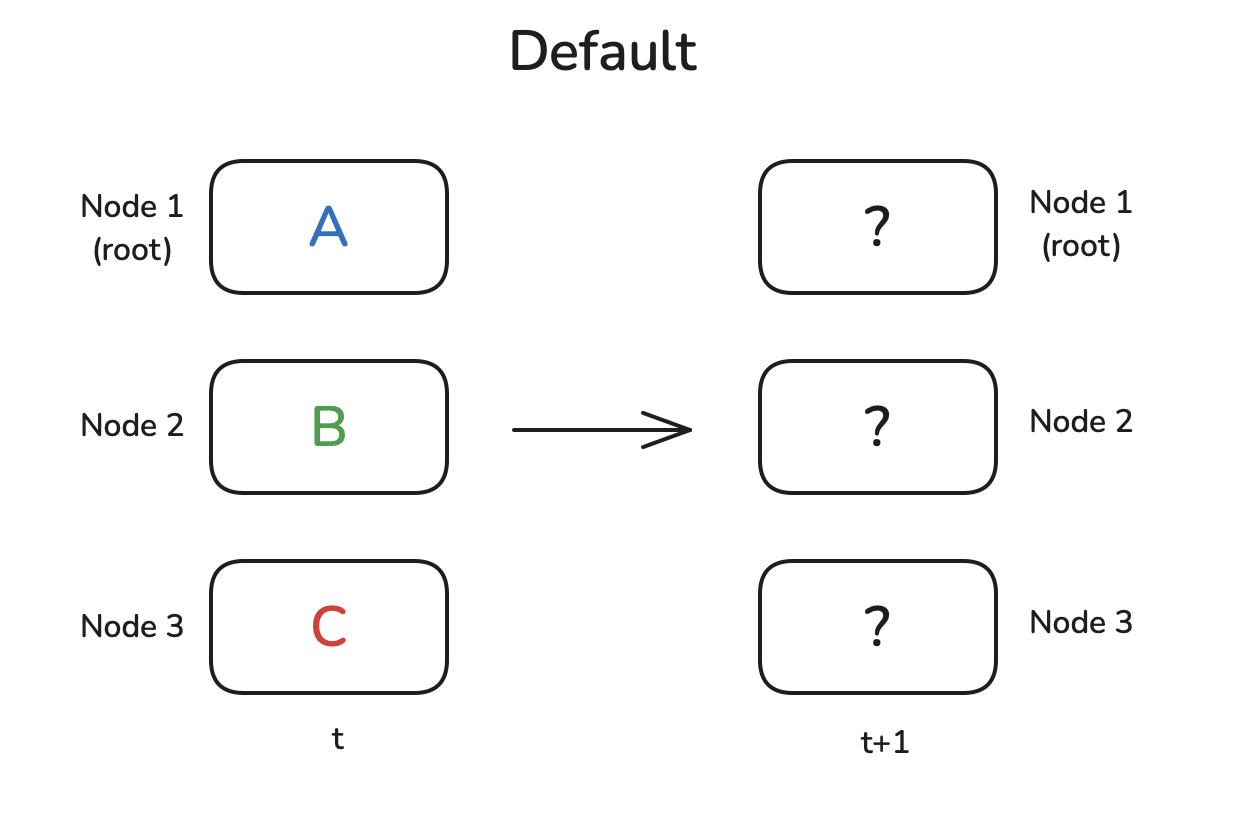
也许我们需要将一个节点的结果发送到所有其他节点，或者需要汇总每个节点的所有中间结果以报告总体结果。通常情况下，有一个具有显著地位的节点在操作中起到核心作用，在这里用 root表示，它是某些操作的目标或源。让我们从最简单的原语之一开始：广播操作 Broadcast。

广播（Broadcast）

一个非常常见的模式是，你在节点1上有一些数据，并希望与所有其他节点共享数据，以便它们可以使用数据进行一些计算。广播操作正是做到了这一点：

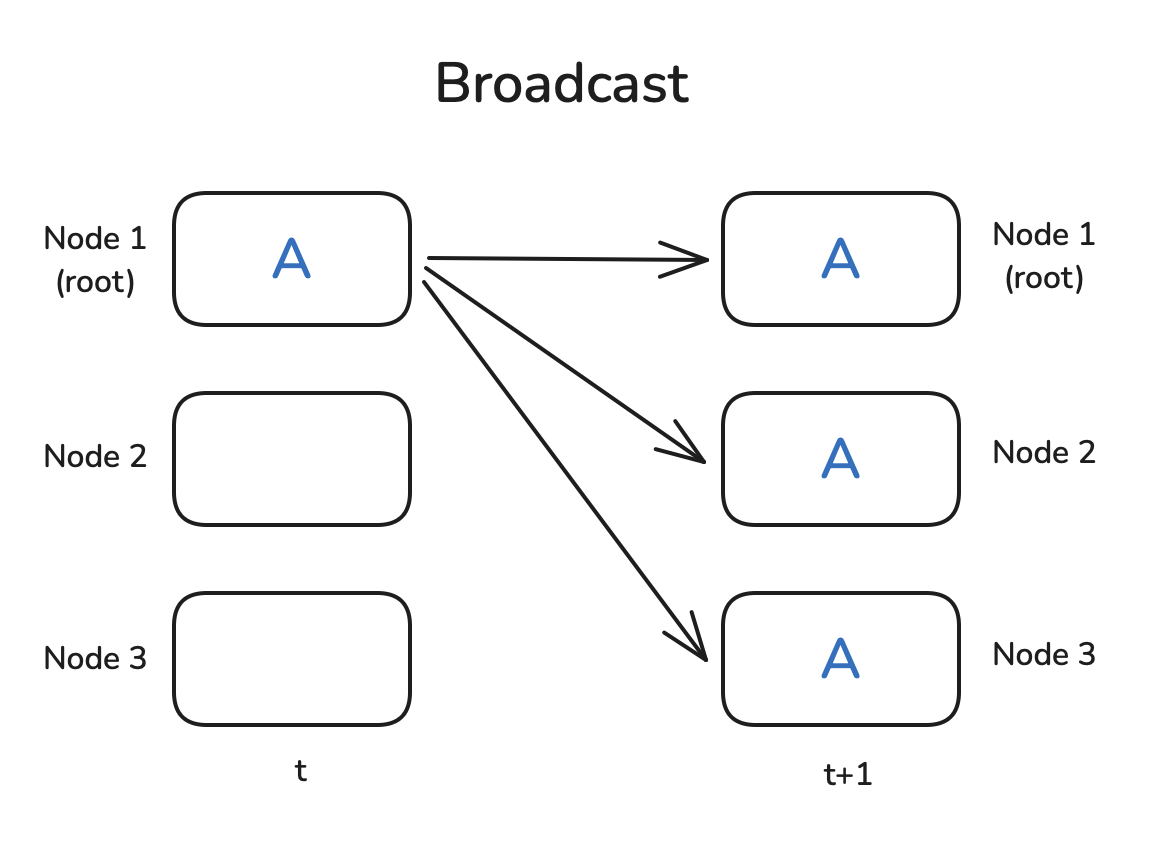
PyTorch原生提供了集合操作 Collective Operation，因此可以很容易地编写一个小例子来演示广播是如何工作的。我们首先需要使用 dist.init_process_group初始化一个进程组，设置通信后端（稍后我们将讨论NCCL），确定存在多少个 Workers（aka Nodes），并为每个工作者分配一个Rank（我们可以用 dist.get_rank获取）。最后，它在工作者之间建立连接。

为了展示 dist.broadcast操作，让我们创建一个张量，在 rank=0上有非零值，并在其他工作者上创建全零张量。然后，我们使用 dist.broadcast(tensor, src=0)将 rank=0的张量分发到所有其他排名：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import torch
import torch.distributed as dist

def init_process():
    dist.init_process_group(backend='nccl')
    torch.cuda.set_device(dist.get_rank())
  
def example_broadcast():
    if dist.get_rank() == 0: # root
        tensor = torch.tensor([1, 2, 3, 4, 5], dtype=torch.float32).cuda()
    else:
        tensor = torch.zeros(5, dtype=torch.float32).cuda()
    print(f"Before broadcast on rank {dist.get_rank()}: {tensor}")
    dist.broadcast(tensor, src=0)
    print(f"After broadcast on rank {dist.get_rank()}: {tensor}")  
init_process()
example_broadcast()

你可以使用 torchrun --nproc_per_node=3 dist_op.py运行上述脚本（你需要3个GPU，或者根据需要更改 nproc_per_node），你应该看到以下输出：

1
2
3
4
5
6
7
Before broadcast on rank 0: tensor([1., 2., 3., 4., 5.], device='cuda:0')
Before broadcast on rank 1: tensor([0., 0., 0., 0., 0.], device='cuda:1')
Before broadcast on rank 2: tensor([0., 0., 0., 0., 0.], device='cuda:2')

After broadcast on rank 0: tensor([1., 2., 3., 4., 5.], device='cuda:0')
After broadcast on rank 1: tensor([1., 2., 3., 4., 5.], device='cuda:1')
After broadcast on rank 2: tensor([1., 2., 3., 4., 5.], device='cuda:2')

很好，看起来正如预期的那样工作。请注意，Rank message可能会以无序的方式打印出来，因为无法控制哪个打印语句首先执行。现在让我们继续进行归约和全局归约模式！

归约 & 全局归约（Reduce & AllReduce）

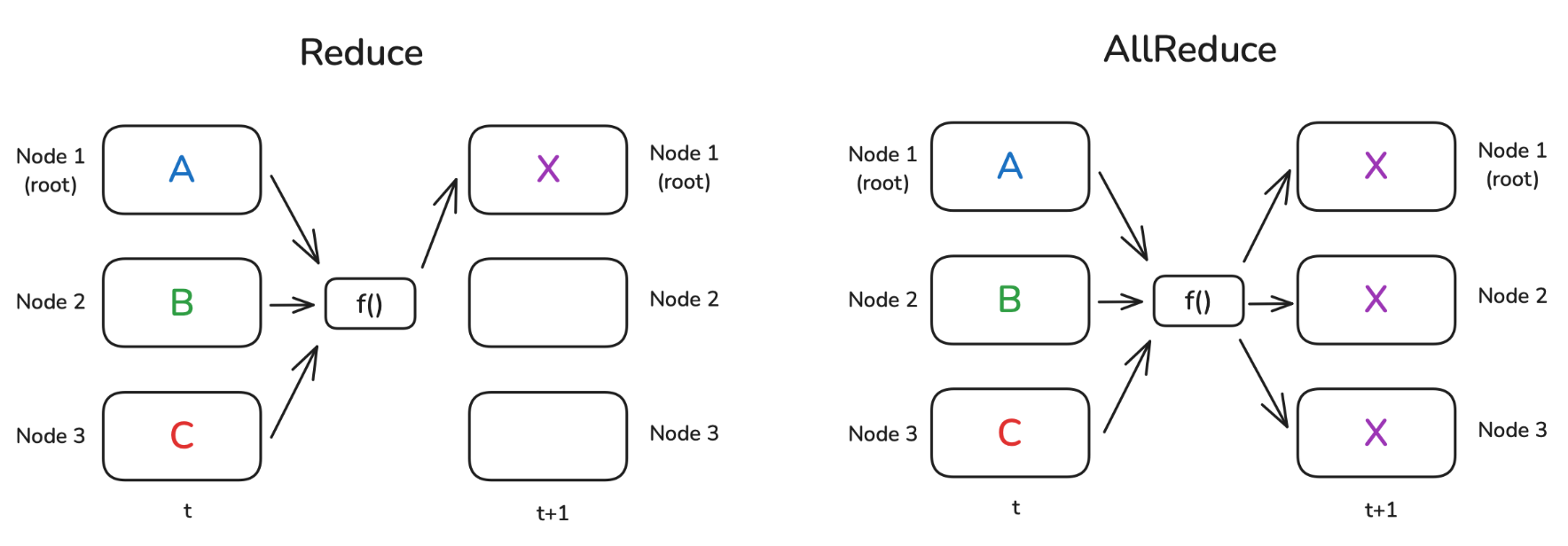
归约模式 Reduce 是分布式数据处理中最基本的模式之一。其思想是通过一个函数 f()（例如求和或平均）来组合每个节点上的数据。在归约 Reduce 的例子中，结果仅发送到 root，而在全局归约 AllReduce 情况下，结果广播到所有节点：

当然，并不存在一种神奇的“自由运行”节点，能够独自完成这样的运算。一般来说，在节点所构成的环形 Ring 或树形 Tree 结构中，每个节点都会进行一部分计算。下面举个简单的例子：假设我们要在每个节点上计算一组数字的总和，并且这些节点以环形方式连接。第一个节点将自身的数字发送给相邻节点，该相邻节点会把接收到的数字与自己的数字相加，然后再转发给下一个相邻节点。当沿着节点环完成一轮传递后，第一个节点将会收到总和。

这是运行简单的Reduce操作来计算张量总和的代码，我们使用 op=dist.ReduceOp.SUM指定要使用的操作（你可以在Pytorch文档 [1] 中找到有关支持操作的更多信息）：

1
2
3
4
5
6
7
8
9
def example_reduce():
    tensor = torch.tensor([dist.get_rank() + 1] * 5, dtype=torch.float32).cuda()
    print(f"Before reduce on rank {dist.get_rank()}: {tensor}")
    # dst=0 代表root节点
    dist.reduce(tensor, dst=0, op=dist.ReduceOp.SUM)
    print(f"After reduce on rank {rank}: {tensor}")
  
init_process()
example_reduce()

请注意，在Reduce操作中，仅更新了 dst节点上的张量：

1
2
3
4
5
6
7
Before reduce on rank 0: tensor([1., 1., 1., 1., 1.], device='cuda:0')
Before reduce on rank 1: tensor([2., 2., 2., 2., 2.], device='cuda:1')
Before reduce on rank 2: tensor([3., 3., 3., 3., 3.], device='cuda:2')

After reduce on rank 0: tensor([6., 6., 6., 6., 6.], device='cuda:0')
After reduce on rank 1: tensor([2., 2., 2., 2., 2.], device='cuda:1')
After reduce on rank 2: tensor([3., 3., 3., 3., 3.], device='cuda:2')

类似地，我们可以执行AllReduce操作（在这种情况下，我们不需要指定目标地点）：

1
2
3
4
5
6
7
8
def example_all_reduce():
    tensor = torch.tensor([dist.get_rank() + 1] * 5, dtype=torch.float32).cuda()
    print(f"Before all_reduce on rank {dist.get_rank()}: {tensor}")
    dist.all_reduce(tensor, op=dist.ReduceOp.SUM)
    print(f"After all_reduce on rank {dist.get_rank()}: {tensor}")
  
init_process()
example_all_reduce()

在这种情况下，结果在所有节点上都可用：

1
2
3
4
5
6
7
Before all_reduce on rank 0: tensor([1., 1., 1., 1., 1.], device='cuda:0')
Before all_reduce on rank 1: tensor([2., 2., 2., 2., 2.], device='cuda:1')
Before all_reduce on rank 2: tensor([3., 3., 3., 3., 3.], device='cuda:2')

After all_reduce on rank 0: tensor([6., 6., 6., 6., 6.], device='cuda:0')
After all_reduce on rank 1: tensor([6., 6., 6., 6., 6.], device='cuda:1')
After all_reduce on rank 2: tensor([6., 6., 6., 6., 6.], device='cuda:2')

现在让我们转向下一个分布式通信操作。在许多实际情况下，每个节点单独执行许多复杂的计算，我们需要在节点之间共享最终结果。Gather和AllGather是我们在这种情况下要使用的操作。让我们来看看！

Gather & AllGather

Gather和AllGather与Broadcast非常相似，因为它们允许在节点之间分发数据而不修改。与Broadcast的主要区别在于，我们不需要从一个节点向所有其他节点共享一个值(aka Broadcast)，而是**每个节点都有一个我们希望收集所有数据的个体数据块（aka Gather）**或在所有节点上收集所有数据的个体数据块（在AllGather的情况下）。一图胜千言，让我们看看：

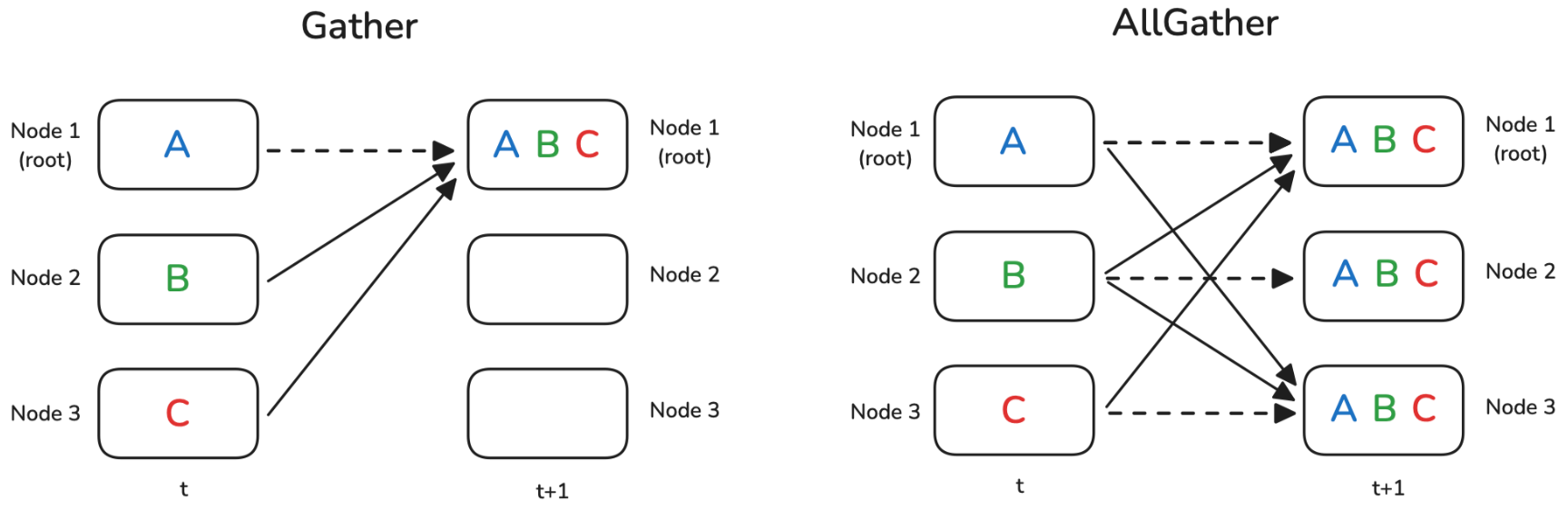
请注意，虚线表示某些数据实际上根本不移动（因为它已经存在于节点上）。

在gather操作的情况下，我们需要准备一个容器对象，用于存储聚合张量，例如 gather_list：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def example_gather():
    tensor = torch.tensor([dist.get_rank() + 1] * 5, dtype=torch.float32).cuda()
    if dist.get_rank() == 0:
        gather_list = [
            torch.zeros(5, dtype=torch.float32).cuda()
            for _ in range(dist.get_world_size())
            ]
    else:
        gather_list = None
    print(f"Before gather on rank {dist.get_rank()}: {tensor}")
    dist.gather(tensor, gather_list, dst=0)
    if dist.get_rank() == 0:
        print(f"After gather on rank 0: {gather_list}")
  
init_process()
example_gather()

我们看到 gather_list确实包含所有排名的张量：

1
2
3
4
5
6
7
Before gather on rank 0: tensor([1., 1., 1., 1., 1.], device='cuda:0')
Before gather on rank 1: tensor([2., 2., 2., 2., 2.], device='cuda:1')
Before gather on rank 2: tensor([3., 3., 3., 3., 3.], device='cuda:2')

After gather on rank 0: [tensor([1., 1., 1., 1., 1.], device='cuda:0'),
                         tensor([2., 2., 2., 2., 2.], device='cuda:0'),
                         tensor([3., 3., 3., 3., 3.], device='cuda:0')]

编者注： dist.gather() 的工作方式确实不需要显式指定 source 的顺序，因为它会自动按照进程的 rank 顺序收集数据。

对于AllGather示例，唯一需要改变的是每个节点都需要一个结果的占位符：

1
2
3
4
5
6
7
8
9
10
11
12
def example_all_gather():
    tensor = torch.tensor([dist.get_rank() + 1] * 5, dtype=torch.float32).cuda()
    gather_list = [
        torch.zeros(5, dtype=torch.float32).cuda()
        for _ in range(dist.get_world_size())
        ]
    print(f"Before all_gather on rank {dist.get_rank()}: {tensor}")
    dist.all_gather(gather_list, tensor)
    print(f"After all_gather on rank {dist.get_rank()}: {gather_list}")
  
init_process()
example_all_gather()

确实，可以看到现在每个节点都有了所有数据：

1
2
3
4
5
6
7
8
9
10
11
12
13
Before all_gather on rank 0: tensor([1., 1., 1., 1., 1.], device='cuda:0')
Before all_gather on rank 1: tensor([2., 2., 2., 2., 2.], device='cuda:1')
Before all_gather on rank 2: tensor([3., 3., 3., 3., 3.], device='cuda:2')

After all_gather on rank 0: [tensor([1., 1., 1., 1., 1.], device='cuda:0'),
                             tensor([2., 2., 2., 2., 2.], device='cuda:0'),
                             tensor([3., 3., 3., 3., 3.], device='cuda:0')]
After all_gather on rank 1: [tensor([1., 1., 1., 1., 1.], device='cuda:1'),
                             tensor([2., 2., 2., 2., 2.], device='cuda:0'),
                             tensor([3., 3., 3., 3., 3.], device='cuda:0')]
After all_gather on rank 2: [tensor([1., 1., 1., 1., 1.], device='cuda:2'),
                             tensor([2., 2., 2., 2., 2.], device='cuda:2'),
                             tensor([3., 3., 3., 3., 3.], device='cuda:2')]

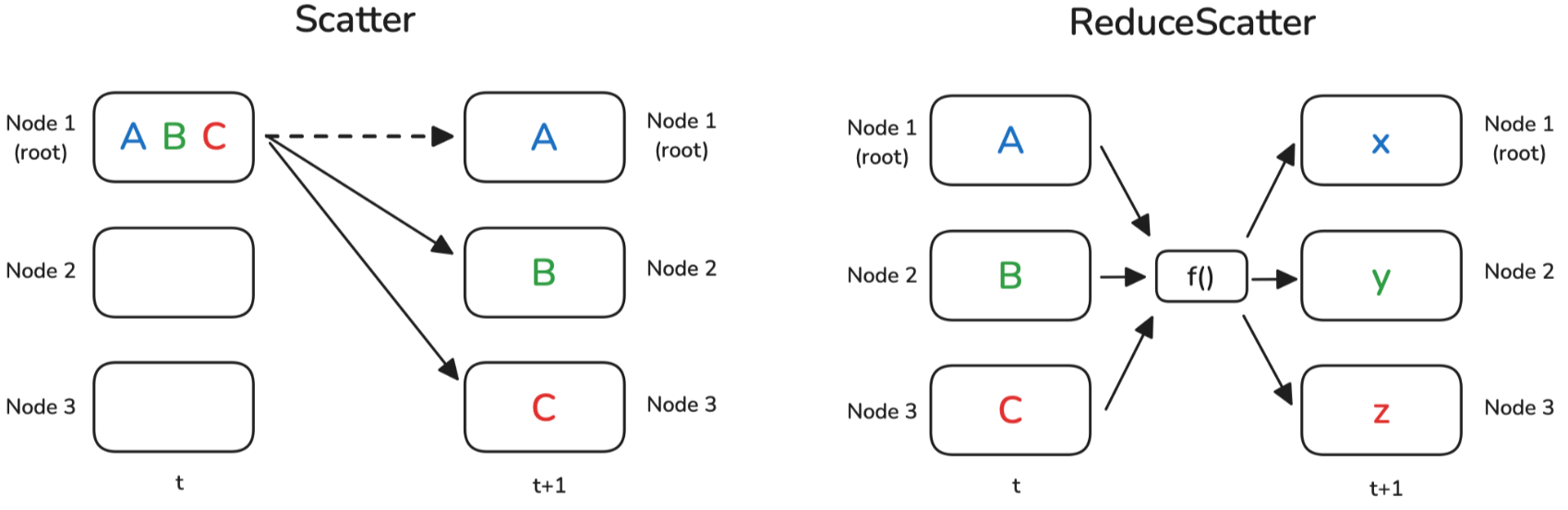
那么反向操作gather又是什么呢？在这种情况下，我们将所有数据都集中在一个节点上，并希望在节点之间分发/切片它，可能还会进行一些中间处理？我们可以使用Scatter，或者在操作之间使用ReduceScatter模式：

Scatter & ReduceScatter

正如名称所暗示的，Scatter操作的目标是将数据从一个节点分发到所有其他节点。因此，它与Broadcast操作不同，后者是复制数据而不进行切片 Slicing，并且它逻辑上是Gather操作的反向。

ReduceScatter模式略微复杂：想象一下，在Reduce情况下应用操作，但我们不仅将结果移动到一个节点，还将其均匀分布到所有节点：

Scatter操作在代码中的表示方式与Gather相反：我们准备源数据作为我们希望分发的张量列表，而不是准备一个张量列表作为目标。还需要指定 src：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def example_scatter():
    if dist.get_rank() == 0:
        scatter_list = [
            torch.tensor([i + 1] * 5, dtype=torch.float32).cuda()
            for i in range(dist.get_world_size())
            ]
        print(f"Rank 0: Tensor to scatter: {scatter_list}")
    else:
        scatter_list = None
    tensor = torch.zeros(5, dtype=torch.float32).cuda()
    print(f"Before scatter on rank {dist.get_rank()}: {tensor}")
    dist.scatter(tensor, scatter_list, src=0)
    print(f"After scatter on rank {dist.get_rank()}: {tensor}")
  
init_process()
example_scatter()

结果显示，空张量已被 scatter_list的内容填充：

1
2
3
4
5
6
7
8
9
10
Rank 0: Tensor to scatter: [tensor([1., 1., 1., 1., 1.], device='cuda:0'),
                            tensor([2., 2., 2., 2., 2.], device='cuda:0'),
                            tensor([3., 3., 3., 3., 3.], device='cuda:0')]
Before scatter on rank 0: tensor([0., 0., 0., 0., 0.], device='cuda:0')
Before scatter on rank 1: tensor([0., 0., 0., 0., 0.], device='cuda:1')
Before scatter on rank 2: tensor([0., 0., 0., 0., 0.], device='cuda:2')

After scatter on rank 0: tensor([1., 1., 1., 1., 1.], device='cuda:0')
After scatter on rank 1: tensor([2., 2., 2., 2., 2.], device='cuda:1')
After scatter on rank 2: tensor([3., 3., 3., 3., 3.], device='cuda:2')

让我们创建更有趣的数据来演示ReduceScatter的逻辑：在每个节点上，我们创建一个包含幂指数和节点排名偏移函数的2元素向量列表（这有点难以想象，所以看下面的示例）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def example_reduce_scatter():
    rank = dist.get_rank()
    world_size = dist.get_world_size()
    input_tensor = [
        torch.tensor([(rank + 1) * i for i in range(1, 3)], dtype=torch.float32).cuda()**(j+1) 
        for j in range(world_size)
        ]
    output_tensor = torch.zeros(2, dtype=torch.float32).cuda()
    print(f"Before ReduceScatter on rank {rank}: {input_tensor}")
    dist.reduce_scatter(output_tensor, input_tensor, op=dist.ReduceOp.SUM)
    print(f"After ReduceScatter on rank {rank}: {output_tensor}")  
  
init_process()
example_reduce_scatter()

让我们打印一下我们创建的数据模式。我们也可以立即看到ReduceScatter的模式：第一个排名接收了每个节点的第一个张量的总和，第二个排名包含了每个节点的第二个张量的总和，依此类推：

1
2
3
4
5
6
7
8
9
10
11
12
13
Before ReduceScatter on rank 0: [tensor([1., 2.], device='cuda:0'),
            tensor([1., 4.], device='cuda:0'),
            tensor([1., 8.], device='cuda:0')]
Before ReduceScatter on rank 1: [tensor([2., 4.], device='cuda:1'),
                                 tensor([ 4., 16.], device='cuda:1'),
                                 tensor([ 8., 64.], device='cuda:1')]
Before ReduceScatter on rank 2: [tensor([3., 6.], device='cuda:2'),
                                 tensor([ 9., 36.], device='cuda:2'),
                                 tensor([ 27., 216.], device='cuda:2')]

After ReduceScatter on rank 0: tensor([ 6., 12.], device='cuda:0')
After ReduceScatter on rank 1: tensor([14., 56.], device='cuda:1')
After ReduceScatter on rank 2: tensor([ 36., 288.], device='cuda:2')

下面简要地看一下一个常见的使用ReduceScatter和AllGather的AllReduce实现：Ring AllReduce。

快速关注Ring AllReduce

环形 Ring AllReduce是AllReduce的一种特定实现，经过优化以实现可伸缩性。与所有设备直接相互通信不同(这可能会造成通信瓶颈)，环形All-Reduce可以分解为两个关键步骤：ReduceScatter和AllGather。它的工作原理如下：

  1. ReduceScatter
    • 每个设备将其数据（例如梯度）分割成块，并将一个块发送给其邻居。同时，每个设备从其另一个邻居接收一个块。
    • 当每个设备接收到一个块时，它将其对应的块添加（减少）到接收到的块中。
    • 这个过程在环中持续进行，直到每个设备持有一个部分减少的块，表示该块的梯度在所有设备中的总和。
  2. AllGather
    • 现在，每个设备需要从其他设备收集完全减少的块。
    • 设备开始将它们的减少块发送给邻居。
    • 每个设备转发收到的块，直到每个设备都有了完全减少的块，使每个设备得到完整的、总结的梯度。

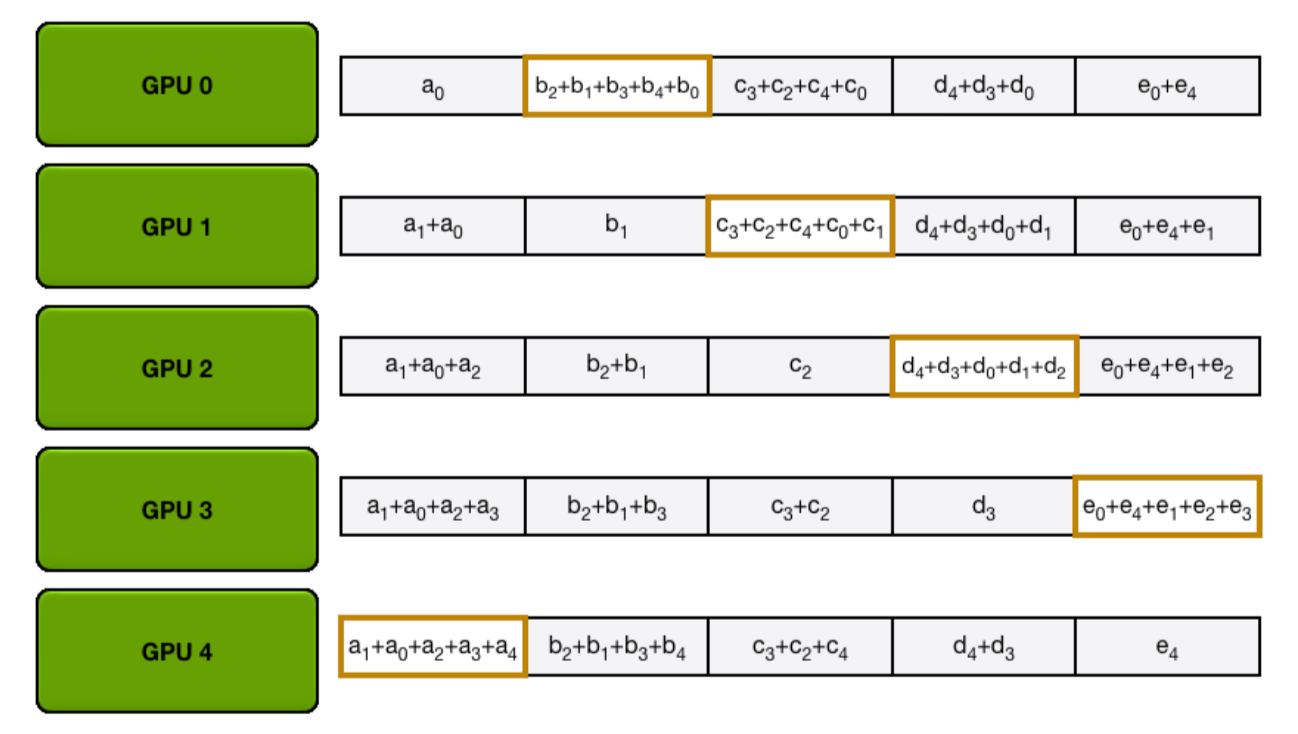
让我们通过以下动画来说明，我们有5个GPU，每个GPU都有长度为5的张量。第一个动画显示了ReduceScatter步骤，最终每个GPU都接收到了特定数据块的减少结果（橙色矩形）：

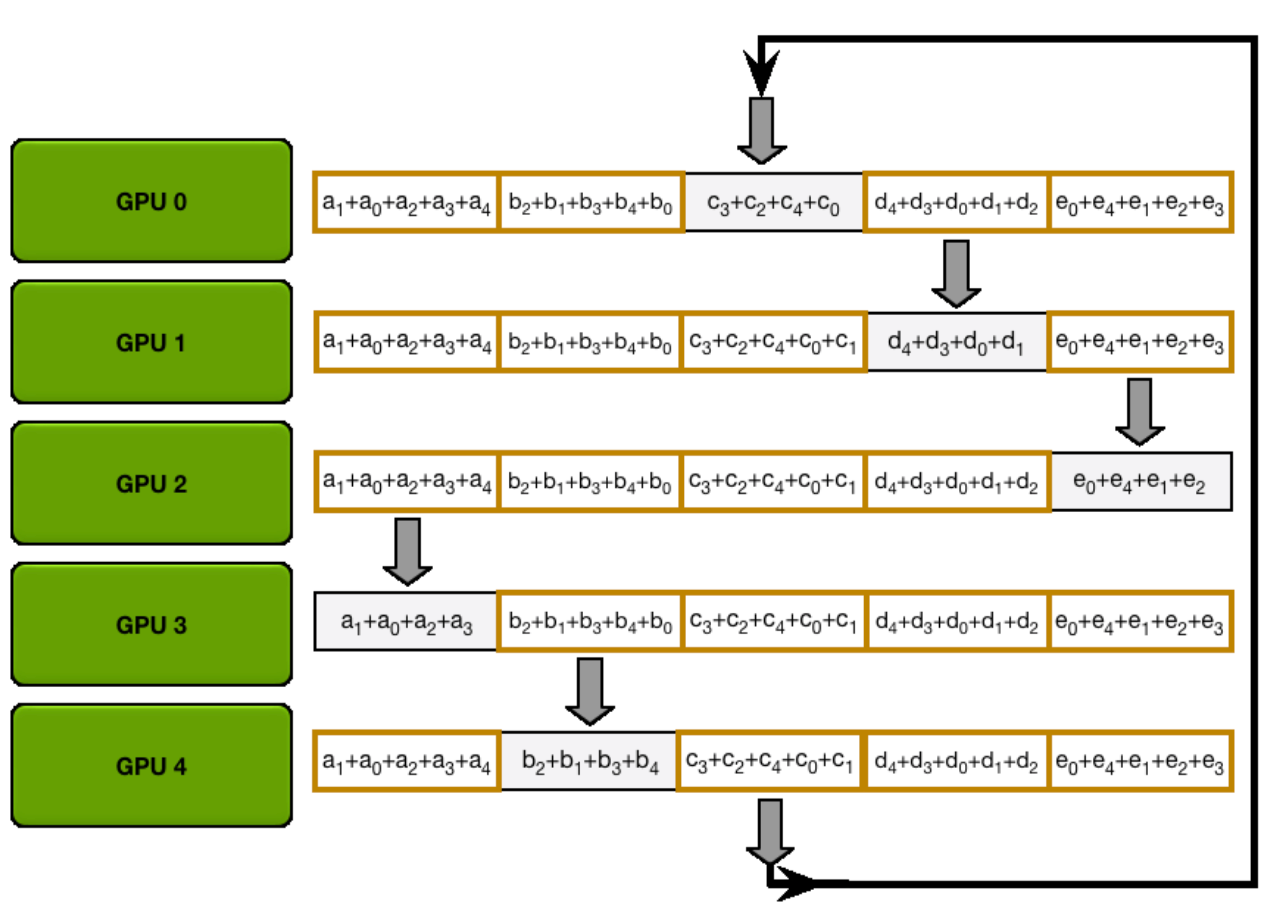
编者注：以下两张均为gif图，建议访问网站来得到更好的阅读体验

接下来的动画展示了AllGather步骤，在此过程结束时，每个GPU获取了AllReduce操作的完整结果(即上文提到的：AllReduce=ReduceScatter + AllGather)：

你可能已经注意到，在reduce-scatter和all-gather步骤中，每个GPU发送和接收值 $N−1$次。每个GPU每次传输发送 $K/N$ 个值，其中 K 是数组长度。因此，每个GPU发送和接收的总数据量为 $2×(N−1)×K/N$。当 N（GPU的数量）较大时，每个GPU发送和接收的总数据量约为2×K，其中 K是总参数数量。

对于AllReduce，有两个关键点需要记住：

  1. 当N（GPU的数量）较大时，AllReduce的通信成本约为2×K。
  2. 一个AllReduce操作可以分解为reduce-scatter和all-gather两个步骤。这两个操作的通信成本是AllReduce的一半，约为K。

正如我们所看到的，即使在节点之间带宽有限的情况下，这种实现也可以有效利用。

现在已经了解了分布式操作的主要构建模块，但在实际操作中让我们看看用于同步的特殊操作之前，来看看一个特殊操作：Barrier。

Barrier 屏障

Barrier是一种简单的操作，用于同步所有节点。直到所有节点都到达Barrier之前，Barrier不会被解除。然后才能继续进行进一步的计算：

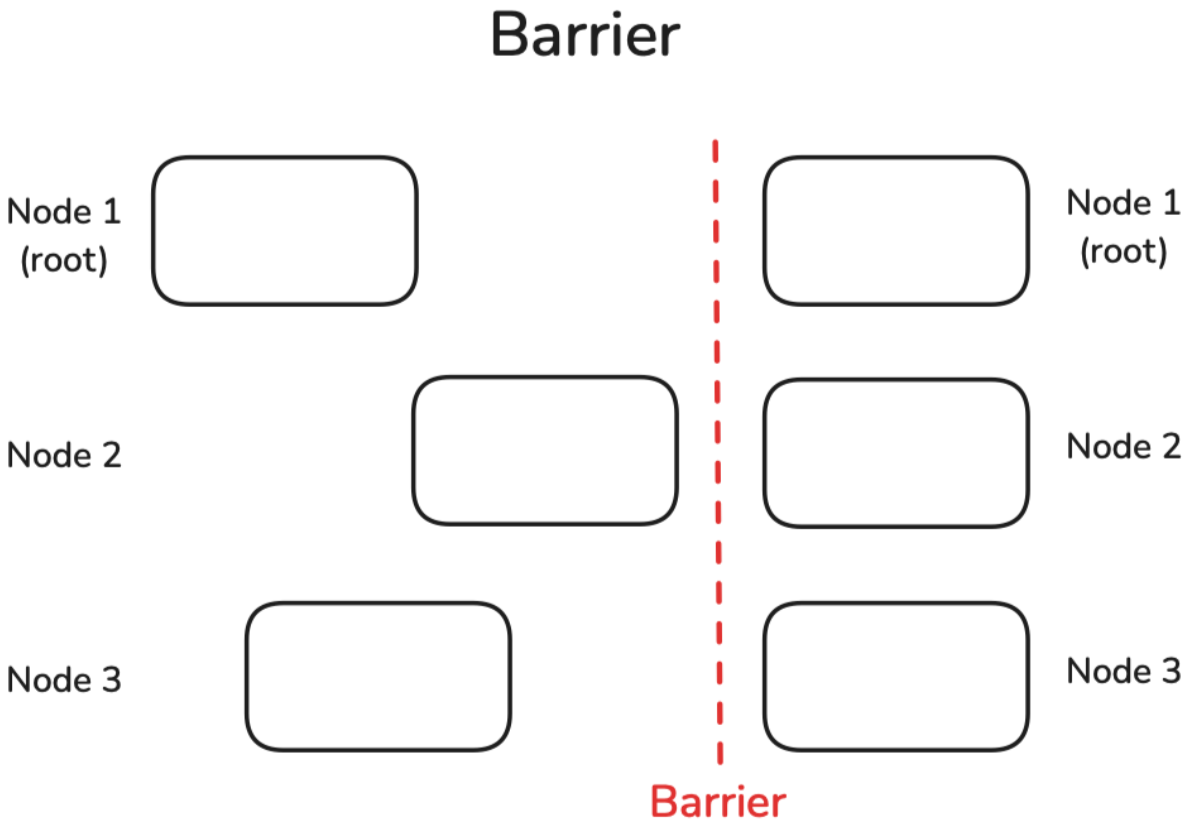
我们可以通过在每个节点上设置不同的睡眠时间来轻松模拟延迟的节点，然后看看它们通过Barrier所需的时间：

1
2
3
4
5
6
7
8
9
10
def example_barrier():
    rank = dist.get_rank()
    t_start = time.time()
    print(f"Rank {rank} sleeps {rank} seconds.")
    time.sleep(rank)  # Simulate different processing times
    dist.barrier()
    print(f"Rank {rank} after barrier time delta: {time.time()-t_start:.4f}")
  
init_process()
example_barrier()

我们可以看到，尽管第一个排名没有睡眠，但它也需要2秒才能通过Barrier：

1
2
3
4
5
6
7
Rank 0 sleeps 0 seconds.
Rank 1 sleeps 1 seconds.
Rank 2 sleeps 2 seconds.

Rank 0 after barrier time delta: 2.0025
Rank 1 after barrier time delta: 2.0025
Rank 2 after barrier time delta: 2.0024

需要小心地进行这种方式的所有节点同步操作，因为这会打败并行独立操作的目的，可能会减慢整个处理速度。在许多情况下，如果快速节点已经开始处理下一个作业，这可能是可以接受的，因为快速节点在下一个迭代中可能会变慢，从而平衡整个过程中的延迟。

在转向实际分布式训练实现之前，先来了解：NCCL到底是什么？

NCCL：NVIDIA 集合通信库

当在许多GPU上训练大型模型时，经常会遇到NCCL！那是什么？

有几个实现集合通信 Collective Communication 的库，并得到PyTorch的支持：有经典的MPI（消息传递接口），有Meta的Gloo，最后还有 NCCL（NVIDIA集合通信库）。它们在集合通信模式方面提供类似的功能，但针对不同的硬件设置进行了优化；NCCL设计用于有效地服务GPU-GPU通信，而MPI和Gloo则设置为CPU-CPU或CPU-GPU通信。PyTorch提供了一个很好的指南 [2] 来决定使用哪一个：

  • GPU训练：使用NCCL
  • CPU训练：使用Gloo

分布式训练性能分析

内核

假设内核已经集成到PyTorch中。作为一个简单的例子，我们可以查看在PyTorch中实现的Layer Normalization函数 torch.nn.functional.layer_norm。有几种方法可以分析此函数的核心。最直接的方法可能是使用Python的 time模块。然而，由于CUDA操作是异步的，使用这种方法测量时间只会捕获Python中启动内核的开销，而不是内核本身的实际执行时间。

为了解决这个问题，可以利用 torch.cuda.Event来进行准确的时间测量，并使用 torch.cuda.synchronize()指令确保等待内核执行完成。以下代码段展示了这种方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def profile_pytorch(func, input):
    # 创建CUDA事件以跟踪时间。CUDA操作是异步的，
    start = torch.cuda.Event(enable_timing=True)  # 事件标记开始时间
    end = torch.cuda.Event(enable_timing=True)    # 事件标记结束时间
    # 预热以消除第一次运行的任何开销，这可能不反映
    # 实际性能。
    for _ in range(10):
        func(input)
    # 在执行函数之前记录开始时间
    start.record()
    func(input)  # 调用我们想要分析的函数
    # 在函数完成后记录结束时间
    end.record()
    # 同步CUDA操作，以确保所有操作完成后再测量
    torch.cuda.synchronize()
    # 计算并返回耗时（毫秒）。
    return start.elapsed_time(end)

更有效的性能分析方法是利用之前介绍的PyTorch Profiler。例如，考虑以下代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import torch
import torch.nn.functional as F

def pytorch_layer_norm(input):
    return F.layer_norm(input, input.size()[1:])

a = torch.randn(10000, 10000).cuda()

with torch.profiler.profile(
    activities=[
        torch.profiler.ProfilerActivity.CPU,  # 分析CPU活动
        torch.profiler.ProfilerActivity.CUDA,  # 分析CUDA活动
    ],
    # 定义分析器的调度
    schedule=torch.profiler.schedule(
        wait=1,      # 在开始分析之前等待1次迭代
        warmup=3,    # 进行3次迭代的预热，以稳定性能
        active=2,    # 进行2次活动迭代的分析
        repeat=1,    # 将分析调度重复一次
    ),
    on_trace_ready=torch.profiler.tensorboard_trace_handler('.'),

) as p:
    for iter in range(10):
        pytorch_layer_norm(a)
        p.step()

# 打印按总CUDA时间排序的汇总分析结果表，限制显示前8个条目
print(p.key_averages().table(sort_by="cuda_time_total", row_limit=8))

这将打印按总CUDA时间排序的汇总分析结果表，输出如下：

你还可以尝试在 chrome://tracing/ 上检查跟踪：

提示

如果你是第一次使用该工具，可以使用右箭头和左箭头键导航跟踪。此外，你还可以按住Alt键，同时使用鼠标左右滚动来放大和缩小。

放大后，可以观察调用 layer_norm 时操作流程的跟踪：

序列从CPU（上部分）开始，使用 aten::layer_norm，然后转到 aten::native_layer_norm，最后过渡到 cudaLaunchKernel。从那里，我们进入GPU，调用 vectorized_layer_norm_kernel 内核。

注意
可以通过将分析器中的 profile_memory 设置为 True 来启用内存分析。但这可能会导致更复杂的跟踪。

虽然PyTorch Profiler提供了快速的性能概述，但NVIDIA Nsight Compute (ncu) 提供了更深入的GPU性能洞察，包括每个内核的详细执行时间和内存使用情况。要运行分析器非常简单：

1
ncu --set full python layer_norm.py

这里的 layer_norm.py 是执行层归一化函数的简单文件。此命令将生成日志输出，但更有效的方法是通过设置输出标志来可视化结果：

1
ncu --set full -o output python layer_norm.py

然后使用Nsight Compute打开文件 output.ncu-rep，你将看到类似于以下的视图：

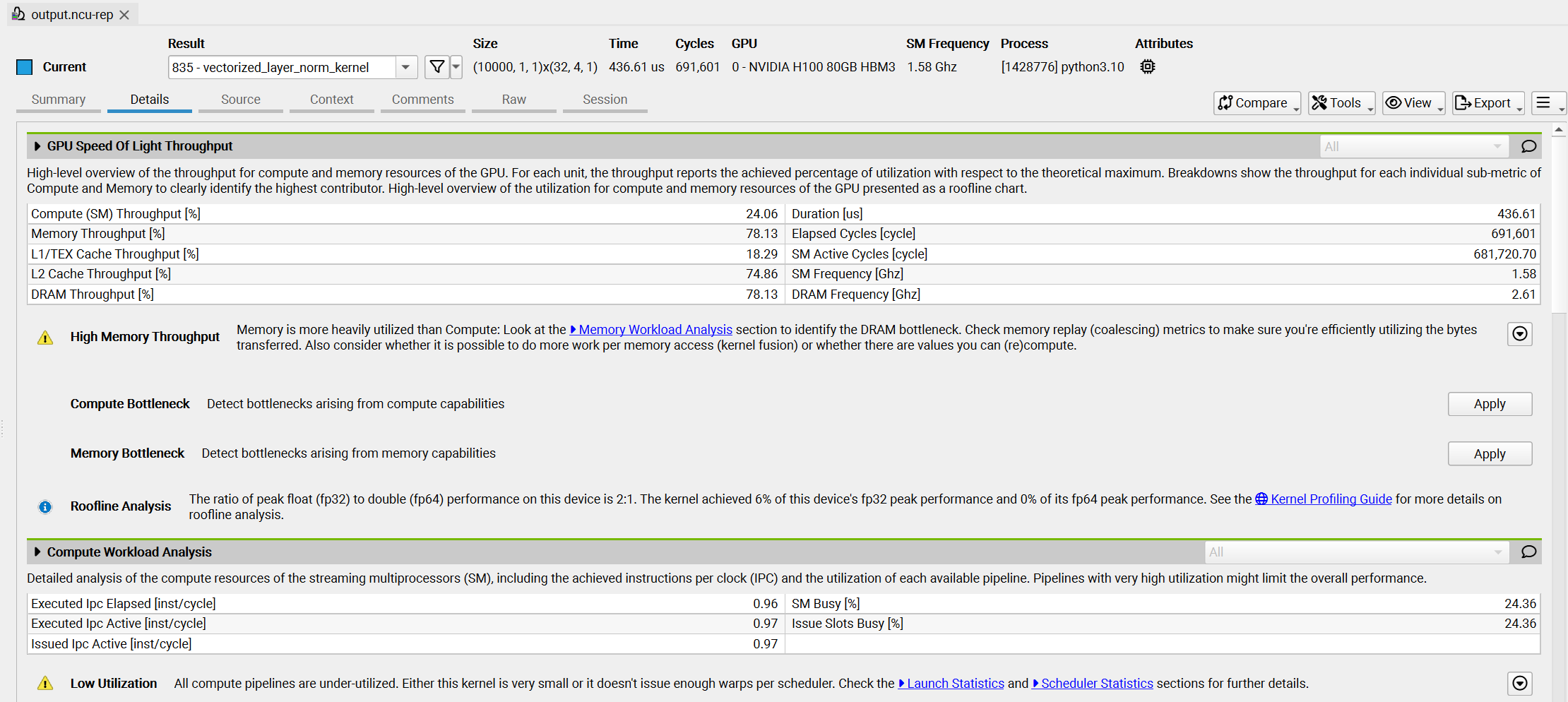
其中清晰地显示了关于计算和内存利用率的警告，以及如何优化内核以实现最大占用率。

CPP扩展

如果要分析的内核尚未集成到PyTorch中，你可以使用PyTorch的 cpp_extension 模块轻松编译和运行自定义CUDA代码。这个过程非常简单 —— 只需在 .cu 文件中创建你的CUDA内核，并使用 cpp_extension 模块中的 load 函数将其加载到Python中。

例如，一个简单的 add 内核的 .cu 文件如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include 
#include 
#include 

__global__ void add_kernel(float* x, float* y, float* output, int size) {
    int index = blockIdx.x * blockDim.x + threadIdx.x;
    if (index < size) {
        output[index] = x[index] + y[index];
    }
}

void add_cuda(torch::Tensor x, torch::Tensor y, torch::Tensor output) {
    int threads = 1024;
    int blocks = (x.size(0) + threads - 1) / threads;

    add_kernel<<>>(x.data_ptr(), y.data_ptr(), output.data_ptr(), x.size(0));
}
PYBIND11_MODULE(TORCH_EXTENSION_NAME, m) {
    m.def("add_cuda", &add_cuda, "Vector addition (CUDA)");
}

以及用于加载内核的Python文件：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import torch
from torch.utils.cpp_extension import load

# 加载并编译CUDA扩展
vector_add = load(
    name="vector_add",
    sources=["add_kernel.cu"],
    verbose=True
)

# 定义输入张量
size = 10000
x = torch.randn(size, device='cuda')
y = torch.randn(size, device='cuda')
output = torch.empty(size, device='cuda')

# 运行CUDA内核
vector_add.add_cuda(x, y, output)

使用这种方法，你可以像之前展示的那样，使用PyTorch的分析器或NVIDIA工具来分析自定义CUDA内核。

计算LLM 训练中的规模

让我们了解LLM训练中的典型尺度。当我们谈论内存或计算时，通常是在计算“元素” - 可以将其视为张量中的数值。要得到实际的内存占用（以字节为单位），你需要乘以每个数字的大小（例如，bf16为2字节，fp32为4字节）。

以下是一些快速的粗略估计：

  • 输入令牌（Input tokens）：对于每个批次，我们处理 $\text{seq} \cdot \text{mbs}$ 个令牌，其中mbs是微批次大小，seq是序列长度。
  • 激活（隐藏状态）（Activations (hidden states)）：对于单个层，隐藏状态张量的大小为 $\text{seq} \cdot \text{mbs} \cdot h$ 个元素。
  • 模型权重和梯度（Model weights and gradients）：模型中的每个权重矩阵（如线性层中的）大约有 $h^2$ 个元素。这是每个权重矩阵的元素数量。梯度与权重的大小相同。
  • 优化器状态（Optimizer states）：对于每个权重矩阵（元素数量为 $h^2$），如果你使用像Adam这样的优化器进行混合精度训练，它会在fp32精度下保留动量和方差状态（ $2 \cdot h^2$），以及主权重在fp32（ $h^2$）。因此，每个权重矩阵的总优化器状态将约为 $6 \cdot h^2$。
  • 总模型参数：对于每个transformer块：
    • 注意力参数：
      • QKV投影： $3h^2$ 参数
      • 输出投影： $h^2$ 参数
    • 带有GLU的MLP参数：
      • Gate和Up Proj： $8h^2$ 参数（2个大小为 $h \times 4h$ 的矩阵）
      • Down Proj： $4h^2$ 参数（1个大小为 $4h \times h$ 的矩阵）
    • 每个块的总参数：使用GLU MLPs时为 $16h^2$，不使用GLU时为 $12h^2$
    • 对于完整模型： $16h^2 \cdot \text{num_layers}$（使用GLU）
    • 额外参数：
      • 输入嵌入： $\text{vocab_size} \cdot h$
      • LM头： $\text{vocab_size} \cdot h$（如果不与输入嵌入绑定）
      • 位置嵌入（如果使用）： $\text{max_seq_len} \cdot h$
  • 前向和反向传递计算（FLOPs）：前向传递的FLOPs的非常粗略的估计为 $2 \cdot \text{num_tokens} \cdot \text{num_params}$。反向传递计算是前者的两倍： $4 \cdot \text{num_tokens} \cdot \text{num_params}$。

计算/通信重叠需要的数学

使用前一节中的公式，我们可以估计在分布式训练中计算和通信何时可以有效重叠。让我们以数据并行（Zero-0）为例。

数据并行DP通信分析

需要通信的总梯度大小为：

  • 梯度 = 参数 ≈ $\text{num_layers} \cdot 16h^2$

在反向传递过程中，这些梯度以Buckets（默认25MB）的形式进行通信。每个桶的AllReduce通信时间为：

$$
t_{\text{comm}} = t_{\text{comm_bucket}} = \frac{\text{bucket_size} \cdot 2(\text{DP} - 1)}{\text{DP} \cdot \text{peak_bw}}
$$

注意：对于带宽计算，我们使用来自 NCCL文档 [3] 的总线带宽公式。这些公式考虑了在计算GPU之间计算有效带宽时的具体通信模式。

编者注： Peak_bw 代表 Peak Bandwidth; DP代表DP度，可以简单理解为有多少卡使用DP。

反向传递的计算时间为：

$$
t_{\text{compute}} = \frac{4 \cdot \text{num_tokens} \cdot \text{num_params}}{\text{peak_flops}}
$$

为了有效重叠，我们需要：

$$
\frac{t_{\text{comm}}}{t_{\text{compute}}} = \frac{\text{num_params}}{2 \cdot \text{num_tokens}} \cdot \frac{\text{DP} - 1}{\text{DP}} \cdot \frac{\text{peak_flops}}{\text{peak_bw}} \leq 1
$$

这个比率有助于确定通信是否会成为训练中的瓶颈。当比率小于1时，通信可以与计算完全重叠。

Zero-3 (FSDP) 通信分析

对于 Zero-3，参数和梯度在 GPU 之间共享。让我们分析一个具有每个大小为 $16h^2$ 参数的 transformer 块的模型的通信模式：

  • 对于前向传播中的每个 transformer 块：
    • AllGather：每个 rank $16h^2/DP$ 字节
  • 对于反向传播中的每个 transformer 块：
    • AllGather：每个 rank $16h^2/DP$ 字节
    • ReduceScatter：每个 rank $16h^2/DP$ 字节
  • 每个块的总通信： $3 \cdot 16h^2/DP$ 字节
  • 整个模型的总通信： $3 \cdot \text{num_layers} \cdot 16h^2/DP$ 字节

AllGather 的通信时间是：

$$
t_{\text{comm}} = 16h^2 \cdot \frac{DP - 1}{DP \cdot \text{peak_bw}}
$$

一个解码器层的前向传播的计算时间是：

$$
t_{\text{compute}} = \frac{32 \cdot \text{seq_len} \cdot \text{mbs} \cdot h^2}{\text{peak_flops}}
$$

为了有效地在计算和通信之间进行重叠，我们需要：

$$
\frac{t_{\text{comm}}}{t_{\text{compute}}} = \frac{1}{2 \cdot \text{seq_len} \cdot \text{mbs}} \cdot \frac{DP - 1}{DP} \cdot \frac{\text{peak_flops}}{\text{peak_bw}} \leq 1
$$

当这个比率小于 1 时，下一层的参数通信可以隐藏在当前层的计算之后。

TP 通信分析

对于张量并行 (TP)，在线性层期间激活值在 GPU 之间被分片。让我们分析通信模式：

  • 对于前向传播中的每个列线性层：
    • AllGather 激活值：每个 rank $seq \cdot mbs \cdot h/TP$ 字节
  • 对于反向传播中的每个列线性层：
    • ReduceScatter：每个 rank $seq \cdot mbs \cdot h/TP$ 字节
  • 对于行线性层反之亦然。每个 transformer 块有 2 个列线性层和 2 个行线性层。
  • 每个块的总通信： $8 \cdot seq \cdot mbs \cdot h/TP$ 字节
  • 整个模型的总通信： $8 \cdot \text{num_layers} \cdot seq \cdot mbs \cdot h/TP$ 字节

让我们分析我们是否可以将一层的收集器通信与下一层线性层的计算重叠。收集操作的通信时间是：

$$
t_{\text{comm}} = \frac{seq \cdot mbs \cdot h \cdot (TP - 1)}{TP \cdot \text{peak_bw}}
$$

而下一个线性层（具有参数 $h^2$）的计算时间是：

$$
t_{\text{compute}} = \frac{2 \cdot seq \cdot mbs \cdot h^2}{TP \cdot \text{peak_flops}}
$$

为了有效重叠，我们希望通信时间小于计算时间：

$$
\frac{t_{\text{comm}}}{t_{\text{compute}}} = \frac{TP - 1}{2 \cdot h} \cdot \frac{\text{peak_flops}}{\text{peak_bw}} \leq 1
$$

这个比率告诉我们我们是否可以成功地将收集器通信隐藏在下一个线性层的计算之后。有趣的是，这个比率仅取决于隐藏大小 $h$ 和张量并行度 TP，而不是序列长度或批量大小。

PP 通信分析

对于流水线并行 (PP)，激活值和梯度在流水线阶段之间进行通信。让我们分析通信模式：

  • 对于前向传播中的每个微批次：
    • 接收和发送激活值： $2 \cdot seq \cdot mbs \cdot h$ 字节
  • 对于反向传播中的每个微批次：
    • 接收和发送梯度： $2 \cdot seq \cdot mbs \cdot h$ 字节
  • 每个Micro Batch的总通信： $4 \cdot seq \cdot mbs \cdot h$ 字节
  • 对于梯度累积步骤 (gas)，总通信： $4 \cdot gas \cdot seq \cdot mbs \cdot h$ 字节

让我们分析我们是否可以将激活值/梯度的通信与下一个 transformer 块的计算重叠。下一个流水线阶段中 transformer 块的计算时间是：

$$
t_{\text{compute}} = \frac{32 \cdot seq \cdot mbs \cdot h^2 \cdot \text{num_layers_in_next_pp}}{\text{peak_flops}}
$$

而 P2P 传输的通信时间是：

$$
t_{\text{comm}} = \frac{seq \cdot mbs \cdot h}{\text{peak_bw}}
$$

为了有效重叠，我们希望：

$$
\frac{t_{\text{comm}}}{t_{\text{compute}}} = \frac{\text{peak_flops}}{32 \cdot h \cdot \text{num_layers_in_next_pp} \cdot \text{peak_bw}} \leq 1
$$

与 TP 类似，这个比率与序列长度和批量大小无关。它取决于隐藏大小 $h$，下一个流水线阶段中的层数，以及计算与硬件 P2P 带宽能力的比率。

编者注：全书结束，感谢阅读。

参考文献

[1] https://pytorch.org/docs/stable/distributed.html#torch.distributed.ReduceOp

[2] https://pytorch.org/docs/stable/distributed.html#which-backend-to-use