机器学习-逻辑回归

接着上篇博客继续，我们发现，概率生成模型最终推导函数，其本质还是寻找参数w和b，所以可以设置一个函数，直接来寻找最优的w和b

$$
f_{w,b}(x)=P_{w,b}(C_1|x)=\sigma(z)\
\sigma(z)=\frac{1}{1+exp(-z)}\
z = w \cdot x+b
$$

相较于线性回归，逻辑回归做的事情便是将 wx+b 放入 sigmoid 函数中，使其输出一直处于0~1之间。

在我们确定了函数之后，便是应该再定义一个损失函数。

假设有一组训练数据，其数据大小为 N，而且分别有自己的类别标签C。给定一组 w 和 b，就可以计算这组w，b下产生上图N个训练数据的概率，$f_{w,b}(x^3)$表示 $x^3$ 属于C1的概率，但是其真实分类为C2，所以要用 $1-f_{w,b}(x^3)$。

$L(w,b)L(w,b)$取得的数值最大的时候，即取得最好的w和b，$w^∗,b^∗ = argmax_{w,b}L(w,b)$

在此我们可以做一个变换，对 $L(w,b)$取对数不影响其单调性，然后再加上符号，单调性与之前的相反，那么就是求 $-lnL(w,b)$ 的最小值。对于 $-lnL(w,b)$，我们可以将其写为

$$
-lnL(w,b) \
= -lnf_{w,b}(x^1)\
=-[\hat yln_{w,b}f(x^1)+(1-\hat y)ln(1-f_{w,b}(x^1))]
$$

其实很好理解，当 $\hat y$ 为 1 的时候

$$
lnf_{w,b}(x)=[1 \cdot ln_{w,b}f(x)+(1-1) \cdot ln(1-f_{w,b}(x))]=lnf_{w,b}(x)
$$

当 $\hat y$为 0 的时候

$$
ln(1-f_{w,b}(x))=[0 \cdot ln_{w,b}f(x)+(1-0) \cdot ln(1-f_{w,b}(x))]=ln(1-f_{w,b}(x))
$$

所以便是有了下图的转化

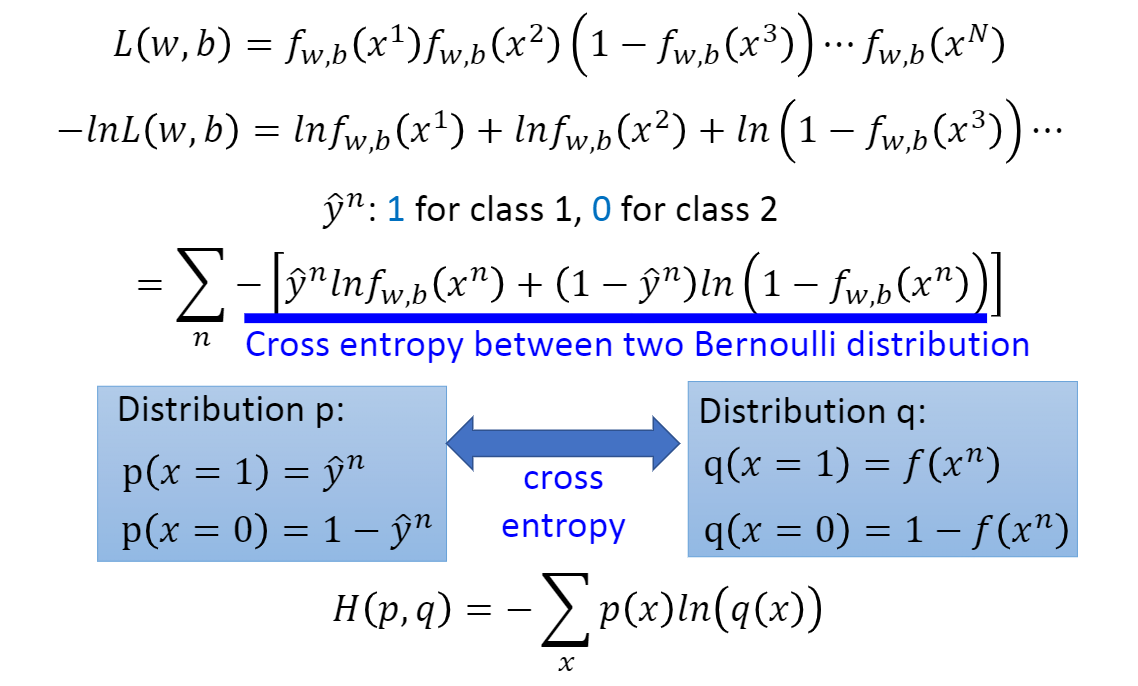
即两个伯努利分布的交叉熵，假设有两个分布 p 和 q，这两个分布的交叉熵就是H(p,q)，交叉熵代表的含义是这两个分布有多接近，如果两个分布是一模一样的话，那计算出的交叉熵就是0，也就是说，当交叉熵为零的时候，说明我们的函数完全符合实际的分布。
如果把function的输出和target都看作是两个伯努利分布，所做的事情就是希望这两个分布越接近越好，交叉熵最小，Loss就最小。

对找最好的function，就是最小化−lnL(w,b)，用梯度下降方法即可。

• 计算算出$lnf_w,_b(x^n)$对$w_i​$​的偏微分
• $​f_w,_b(x)$​可以用 $\sigma{(z)}$​表示，而z可以用 ​$w_i$ ​和 $b $表示，所以可以利用链式法则展开
• 计算 $​ln(1-f_{w,_b}(x^n))$ 对 $​w_i$​的偏微分
• 继续使用链式法则进行计算

$(lnx)^′=\frac{1}{x}$，sigmoid函数求导：$\sigma(x)^′=\sigma(x)⋅(1−\sigma(x))$

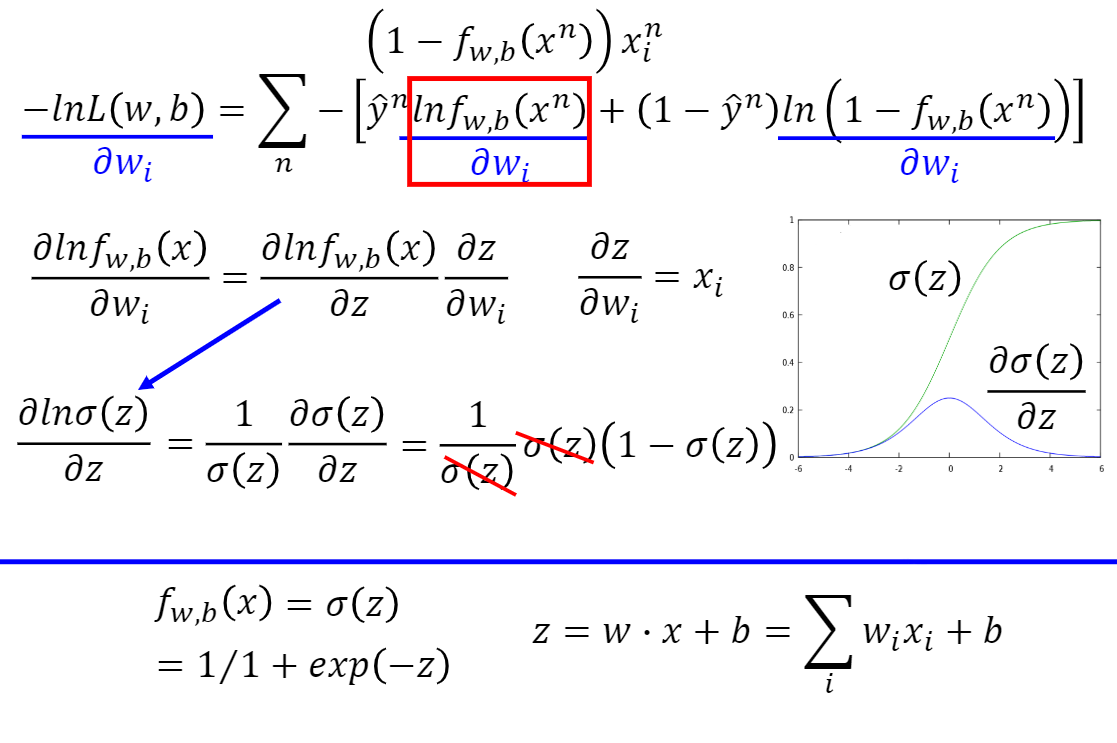
下图则为最终的结果：

得到了梯度之后，便是可以再度使用梯度下降进行 $w_i$ 的更新。对于 Loss 函数的选择，我们使用交叉熵作为其损失。

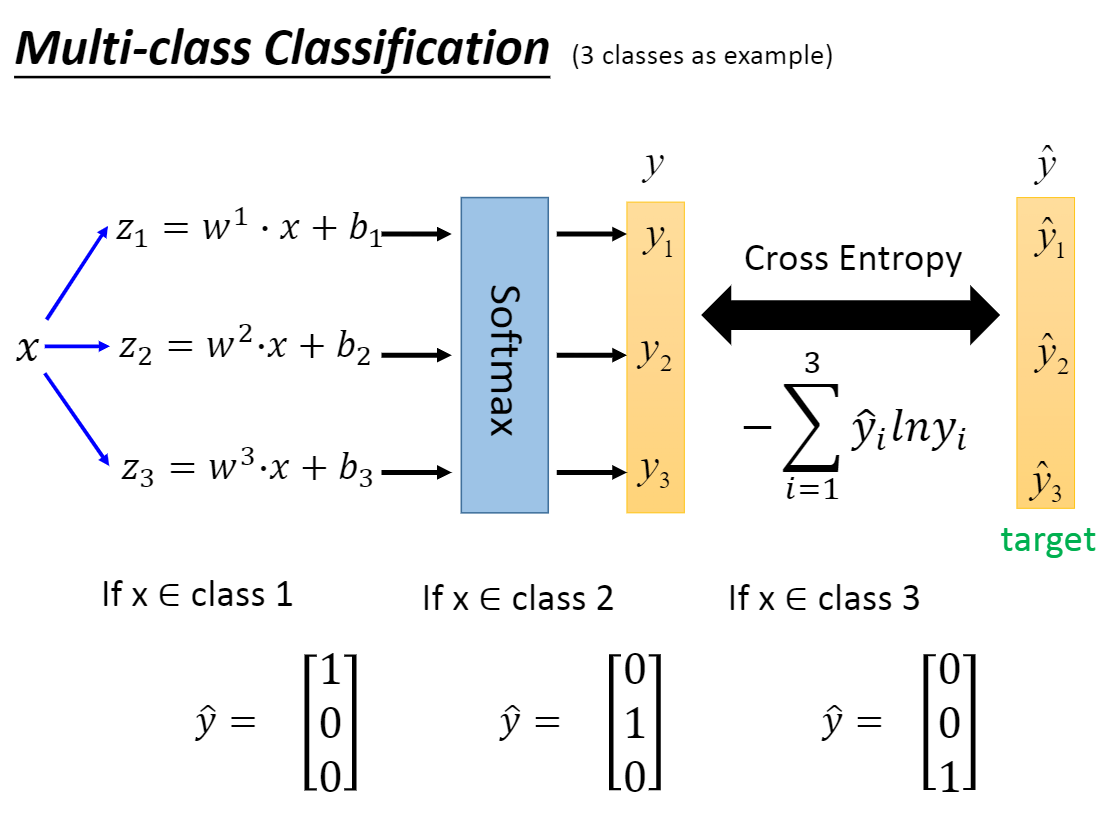
上面说的是二分类问题，对于多分类应该如何解决呢？